Свойства
Замечание: во
всех формулах этого раздела предполагается,
что 
—
целые числа.
Любое целое число является делителем нуля, и частное равно нулю :
Любое целое число делится на единицу:
На ноль делится только ноль:
,
причём частное в этом случае не определено.
Единица делится только на единицу:
Для любого целого числа
найдётся
такое целое число 
для
которого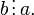 
Если и
то 
Отсюда
же следует, что если
и
то 
Для того чтобы необходимо и достаточно, чтобы
Если
то 
Свойство делимости является отношением нестрогого порядка и, в частности, оно:
рефлексивно, т.е. любое целое число делится на себя же:
транзитивно, т.е. если и
то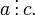 
антисимметрично, т.е. если и
то
либо 
либо 
Алгоритм Евклида для целых чисел
Пусть и — целые числа, не равные одновременно нулю, и последовательность чисел
определена
тем, что каждое 
—
это остаток от деления предпредыдущего
числа на предыдущее, а предпоследнее
делится на последнее нацело, то есть
Тогда
НОД(a,b),
наибольший общий делитель
и
,
равен 
,
последнему ненулевому члену этой
последовательности.
Существование таких 
,
то есть возможность деления с
остатком
на
для
любого целого
и
целого 
,
доказывается индукцией по m.
Корректность этого алгоритма вытекает из следующих двух утверждений:
Пусть
,
тогда НОД (a, b) = НОД (b, r).
Доказательство
НОД(0, ) = для любого ненулевого (т.к. 0 делится на любое целое число, кроме нуля).
Проще сформулировать алгоритм Евклида так: если даны натуральные числа и и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.
Пример
Для иллюстрации, алгоритм Евклида будет использован, чтобы найти НОД a = 1071 и b = 462. Для начала, от 1071 отнимем кратное значение 462, пока не получим знаменатель меньше чем 462. Мы должны дважды отнять 462, (q0 = 2), оставаясь с остатком 147
1071 = 2 × 462 + 147.
Затем от 462 отнимем кратное значение 147, пока не получим знаменатель меньше чем 147. Мы должны трижды отнять 147 (q1 = 3), оставаясь с остатком 21.
462 = 3 × 147 + 21.
Затем от 147 отнимем кратное значение 21, пока не получим знаменатель меньше чем 21. Мы должны семь раз отнять 21 (q2 = 7), оставаясь без остатка.
147 = 7 × 21 + 0.
Таким образом последовательность a>b>R1>R2>R3>R4>...>Rn в данном конкретном случае будет выглядеть так:
1071>462>147>21
Так как последний остаток равен нулю, алгоритм заканчивается числом 21 и НОД(1071, 462)=21.
Описание расширенного алгоритма Евклида. Пусть а и b — натуральные числа, a d — их наибольший больший общий делитель. Расширенный алгоритм Евклида подсчитывает не только d, но и два целых числа x и y, таких, что: ax+by =d. Алгоритм Евклида состоит из последовательности делений с остатком. Наибольший общий множитель представляет собой последний ненулевой остаток в этой последовательности.
РАСШИРЕННЫЙ АЛГОРИТМ ЕВКЛИДА
Алгоритм Евклида можно расширить для нахождения по заданным a и b таких целых x и y, что ax + by = d, где d – наибольший общий делитель a и b.
Пусть для положительных целых чисел a и b (a > b) известны g = НСД(b, a modb), а также числа x’ и y’, для которых
g = x’ * b + y’ * (a mod b)
Поскольку a mod b = a – 
* b, то
g = x’ * b + y’ * (a – * b) = y’ * a + (x’ – y’ * ) * b = x * a + y * b,
где обозначено x = y’, y = x’ – y’ * .
Пусть gcdext(int a, int b, int *d, int *x, int *y) – функция, которая по входным числам a и b находит d = НСД(a, b) и такие x, y что d = a * x + b * y. Для поиска неизвестных x и y необходимо рекурсивно запустить функцию gcdext(b, a mod b, d,x, y) и пересчитать значения x и y по выше приведенной формуле. Рекурсия заканчивается, когда b = 0. При b = 0 НОД(a, 0) = a и a = a * 1 + 0 * 0, поэтому полагаем x = 1, y = 0.
Пример 2.1. Найдем решение уравнения 5x + 3y = 1. Вычисление НОД(5, 3) и нахождение соответствующих x, y произведем в таблице:
-
a
b
x
y
5
3
-1
2
3
2
1
-1
2
1
0
1
1
0
1
0
Из таблицы находим, что НОД(5, 3) = 5 * (-1) + 3 * 2 = 1, то есть x = -1, y = 2.