7.Індуцыраваная тапалогія . Падпрастора тапалагічнай прасторы

Азн. Няхай А падмн-ва тапал. пр-ры (Х,τ) , індуцыраванай тапалогіяй на мн-ве А наз. сукупнасць 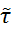(ці _A ) , дзе 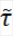={U A|UЄτ}

U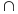 A –Адбітак . Індуцыраваная на мн-ве А тапалогія – сукупнасць адбіткау па ім усіх мн-ау , адкрытых у пр-ры (Х,τ)

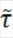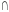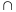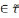
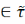Сцв. Індуц. тапалогія на _A есць тапалогія на мн-ве А. Доказ: 1)Ø=Ø AЄ , A= X A _A

2) Няхай {v₂} , αЄI сукупнасць мн-ау , з , для всех αЄI . 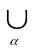v_α= U(Uα A)=(UU_α) AЄ

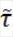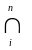3) Няхай v_i , i=1,n , мн-вы з сукупнасці т.е. v_iЄ , для всех i=1,m . Маем : (U_i A)=( U_i) AЄ 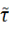(па азн. ).

Тапал. пр-ра (А,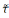 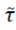) наз. падпр-рай тапалаг. пр-ры (Х, ) , часам яе абазн праз А . Мн-ва , якія уваходзяць у склад тапалогіі наз. адкрытым у гэтай падпр-ры . Такім чынам VЄ _A  V=U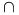 A, дзе UЄτ_x . Мн-ва , якія з'яул. дапауненнямі адкрытых у падпр-ры мн-ау да носьбіта падпр-ры наз. замкнутымі у падпр-ры А. абазн. праз 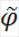(ці 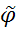(_A) . Такім чынам FЄ _A  A\FЄ _A.

8. Пункты дакранання і вонкавыя пункты мноства.

Наваколлем пункта х з пр-ры Х будзем наз. усякае адкрытае у пр-ры Х мн-ва w(x) , якое змяшчае п. х . (w(x)Єτ_x , xЄw(x))

Прыклад:Шар B(x,τ) есць наваколле пункта х м.п. (x,p) , а замкнуты шар D(x,r) не есць наваколле п. Х

Няхай А не пустое падмн-ва (Х,τ). п. хЄХ наз. пунктам дакранання мн-ва А, калі кожнае яго наваколле w(x) цалкам змяшчае прынамсі адзін пункт мн-ва А (w(x) A≠Ø) Сукупнасць усіх пунктау дакранання мн-ва і абазн. праз . Пункт х пр-ры Х наз. вонкавым пунктам мн-ва А, калі ен не з'яул. яго пунктам дакранання. Гэта значыць, калі існуе яго наваколле w(x) , якое не змяшчае ні аднаго пункта мн-ва А . Сукупнасць усіх вонкавых пунктау мн-ва А наз вонкавасць мн-ва . абазн. ExtA.

Найпрасцейшыя роўнасці і ўключэнні:

1)Х=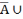 ExtA.

2) ExtA=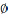 . Вынік: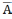 =Х\ExtA, ExtA=X\ .

3)A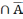⊂ (A =A).

4)ExtA⊂X\A

9. Унутранныя пункты і гранічныя пункты дакранання.

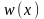Пункт наз. яго унутранным пунктам, калі існуе наваколле пункта х, якое цалкам змяшчаецца ў мн-ве А. Сукупнасць усіх унут-ранных пунктаў мн-ва А наз. яго унутраннасцю і абазначаецца праз Int A ( ).

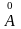Пункт наз. гранічным ці межавым пунктам дакранання мн-ва А, калі ён не з’яўл. ўнутранным, г.зн. па іншаму, што калі адвольнае яго наваколле перасякаецца як з мн-вам А так і з мн-вам Х\А. Сукупнасць усіх гранічных пунктаў мн-ва А наз. мяжой (граніцай) мн-ва А і абазначаецца Fr A ( ).

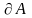Прыклад. .

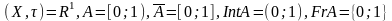Прасцейшыя роўнасці і ўключэнні:

_1.

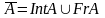
2. .

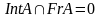3. 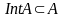(кожны унутранны пункт мноства належыць гэтаму мноству).

4. .

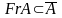10. Лімітавыя і ізаляваныя пункты дакранання.

Пункт наз. лімітавым пунктам мн-ва А, калі ўсякае яго на-ваколле змяшчае прынамсі адзін пункт мн-ва А, які адрозні-ваецца ад х. Сукупнасць усякіх лімітавых пунктаў мн-ва А наз. вытворным мноствам мноства А і абазначаецца ( ).

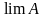Пункт наз. ізаляваным пунктам мн-ва А, калі ён не з’яўл. яго лімітавым пунктам, г.зн. па іншаму, калі існуе яго наваколле , якое не змяшчае ні аднаго пункта з мн-ва А, які адрозніваецца ад х. Сукупнасць усіх ізаляваных пунктау мн-ва А абазначаецца праз IsolA.

Прыклад. .

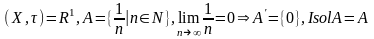Прасцейшыя роўнасці і ўключэнні:

1. .

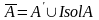2. .

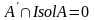3. .

4. (кожны ізаляваны пункт мн-ва належыць гэтаму мн-ву).