35.Кампактныя мн-вы у эўклідавых пр-рах.

Т.(крытэрый кампактнасці у эўкл. пр-ры).Падмн-ва А эўкл. пр-ры Rⁿ з’яўл.кампактнай у ёй мн-вам т. і т. тады калі яна адначасова замкнутае і абмежаванае у ёй мн-ва.

Д-з.=>)так як Rⁿ –м.п. доказ => з тэарэмы(кампактныя мн-вы ў м.п.)

<=)=> з лемы.

Лема.n-мерны пункт kⁿ=[a,b]×…×[a,b].Ёсць кампактнае мн-ва ў Rⁿ.

Д-з лемы (n=2). <=)Няхай -адкрытае пакрыццё k² у R².Прапануем працілеглае k² некампактнае мн-ва,значыць з пакрыцця  нельга выбраць канечнае,раздзелім квадрат k на чатыры часткі срэднімі лініямі,тады прынамсі адзін з гэтых новых падквадратаў k₁² нельга пакрыць канечнай колькасцю з пакрыцця  паўтарым працэдуру для квадрата k₁²,тады прынамсі адзін з падкавдратаў k₂² нельга пакрыць канечнай колькасцю з пакрыцця .Працягваючы працэдуру да бясконцасці атрымаем бясконцую сукупнасць укладзеныя адзін у адзін квадратаў. k² k₁² k₂²… ні адзін з якіх нельга пакрыць канеч. кольк. мн-ваў з пакрыцця ,але агульны пункт x усіх гэтых квадр.,відавочна можа быць пакрыта нейкім мн-вам U г.зн.існуе k_і² ,k_і+1² … якія можна пакрыць адным мн-вам U з пакрыцця ?!=>)Няхай А абмежаванае і замкнутае мн-ва ў Rⁿ.Паколькі А абмежаванае,яго можна уключыць у некаторы куб kⁿ(Аkⁿ)пр-ры Rⁿ,так як па леме куб kⁿ камп.мн-ва атрымоўваем,што А замкнутае падмн-ва камп падпр-ры(kⁿ,_Rⁿ)=> А камп. мн-ва Rⁿ.

36.Уласцівасці камп. Пр-раў і мн-ваў.

Т.1.Няхай (х,_х) камп. пр-ра і f: (х,_х) (у,_х) непарыўная сюр’екцыя.Тады у- камп. пр-ра.

Д-з.Няхай _у={___у, У}адвольнае адкрытае пакрыццё пр-ры У.У=аб’яднанне па  _.Тады _х={ f ^-1 (_) У}-адкрытае пакрыццё пр-ры Х.

1) f ^-1 (_)-адкрытае мн-ва ў Х.

(f ^-1 (_)_х)для адвольнага У,як правобраз адкрытага у У мн-ва _ пры непарыўным адл-ні f.

2) аб’яднанне па У,f ^-1 (_)=Х паколькі f сюр’екцыя.

Т.1’. Няхай А – кампактнае падмноства прасторы Х і f – непарыўнае адлюстраванне f:X→Y=> f(a) кампактнае падмноства прасторы Y.

Т.2. Аб’яднанне канечнай колькасці адвольных кампактных мн-ваў – есць кампакт.мн-ва.

Т.3. Перасячэнне адвольнай колькасці кампактных ў Rⁿ мностваў – кампактнае мноства.

37*. Прамы здабытак прастораў.

Няхай (Х,τ_х),(У,τ_у) тапалагiчныя прасторы. Х У=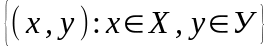

дэкартавы здабытак мностваў Х iУ.

Разгледзем сукупнасць мностваў β= . Тапалогiя τ_ХхУ, якая спараджаецца на мностве Х У базай β называецца здабыт-кам тапалогii τ_х i τ_у. Можна пiсаць τ_ХхУ = =τ_х τ_у. Такiм чы-нам, у тапа-логiю τ_ХхУ уваходзяць Ø (Ø=Ø Ø), Х У(Х τ_х,У τ_у), а таксама ўсе магчымыя аб’яднаннi здабыткаў мностваў адкрытых у Х i мностваў адкрытых у У.

Першым здабыткам тапалагiчных прастор (Х,τ_х),(У,τ_у) называ-ецца прастара (Х У, τ_ХхУ).

Сцверджанне1 Х У ~ У Х (Х,У-прасторы) .

Доказ: На самай справе ƒ: Х У Х Х, ƒ ((х,у))=(х,у)-гамеамар- фiзм.

Сцверджанне2 Калi β₁- база тапалогii прасторы Х (β₁= ),

а β₂-база тапалогii прасторы У (β₂= ), тады β^*= β₁ β₂=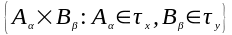 - ёсць база тапалогii здабыткаў прасто-раў Х i У.

Сцверджанне3 Калi Х₁~Х₂ ,У₁~У₂ Х₁ У₁ ~ Х₂ У₂.

Прыклады прамых здабыткаў прастораў.

‌‌‌‌‌‌1) R¹ R¹=‌ R²

а) R¹ R¹, R² - R R

б)

β^*= β β={(a,b) (c,d): a, b, c, d R, a<b, c<d}

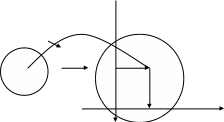
2) S¹хS¹=T² (тапалогiяй на S¹ i T² iндуцыраваная тапалогiяй R³

На самай справе:

а) зафiксуем на кругавым торы Т² мерадыян Х i паралель У. Тады для М Т² можна задаць парай пунктаў (х,у), дзе х Х, ёсць пункт перасячэння паралелi, што праходзiць праз пункт М з мерадыянам Х, а у У ёсць пункт перасячэння мерадыяна, што праходзiць праз пункт М з паралеллю У. Такiм чынам,

Т²= Х У={(х,у): х Х, у У } (роўнасць запiсана для мностваў).

б) Можна паказаць, што 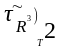= 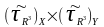. Яны маюць

аднолькавую базу, якая складаецца з крывалiнейных адкрытых

прамавугольнiкаў.

в) Улiчваючы, што Х~ S¹,Y~ S¹ 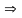T¹=X Y ~ S¹ S¹. Такiм чынам

формула абгрунтавана на ўзроўню прастораў.

Заўвага Аналагiчным чынам атрымоўваецца, што Тⁿ= .

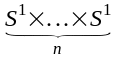Тⁿ- n-мерны тор, з n экзэмпляраў S¹.

38^*. ПРАЕКЦЫI НА КААРДЫНАТНЫЯ ПРАСТОРЫ. У адносiнах да здабытку прастораў Х У, прасторы Х,У называюць каардынатнымi прасторамi. Праекцыямi здабытка Х У на каардынатныя прасторы Х,У называюць наступныя адлюстраваннi адпаведна:

,

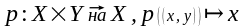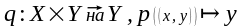
Сцв.1 Праекцыi p,q ёсць непарыўныя адлюстраваннi.

Доказ: Няхай U-адвольнае адкрытае мноства у Х ( U ).

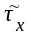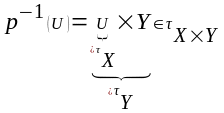. Непарыўнасць p даказана. Аналагiчна даказваецца непарыўнасць праекцыi q.⊠

Адлюстраванне ƒ:Z X Y спараджае адлюстраваннi:

ƒ_Х:Z X ,ƒ_X =pƒ, ƒ_Y: Z Y, ƒ_Y =qƒ, якiя называюцца кампанентамi фдлюстравання ƒ адносна прастораў Х i У адпаведна.

Прыклад Няхай ƒ:R¹ R¹ R¹ , ƒ(t)=(x(t),y(t)). ƒ:x=x(t),y=y(t), t R¹.Z=R¹, X=R¹, Y=R¹. ƒ_Х:R¹ R¹ , x=x(t) , ƒ_Y:R¹ R¹, y=y(t).

Сцв.2Адлюстраванне ƒ прасторы Z у прастору Х У (ƒ:Z Х У) непарыўна калi i толькi калi яго кампаненты ƒ_Х , ƒ_Y непарыўныя адлюстраваннi.

Доказ: Неабходнасць. Калi ƒ непарыўнае адлюстраванне, тады ƒ_X =pƒ,ƒ_Y =qƒ вiдавочна непарыўныя адлюстраваннi, як кампазiцыя непарыўных адлюстраванняў.

Дастатковасць. Няхай ƒ_Х , ƒ_У -непарыўныя адлюстраваннi. Пакажам, што ƒ:Z Х У непарыўнае. Няхай , адвольнае адкрытае мноства ў прамым здабыткуХ У ( ).

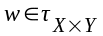Трэба паказаць, што ƒ^-1(w) ,U_α V_β=(U_α Y) (X V_β).Таму маем,

ƒ^-1(w)= ƒ^-1(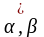 ((U_α Y) (X V_β)))= ƒ^-1 ((U_α Y) (X V_β))=

= ( ƒ^-1 ((U_α Y)) ƒ^-1( (X V_β)))= (( ƒ^-1p^-1(U_α)) ( ƒ^-1q^-1(V_β)))=

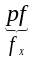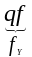= ((( )^-1(U_α)) (( )^-1(V_β)))= ( ) .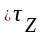