22*. Ліміт паслядоунасці элементаў тп.

Азн. Лімітам бясконцай паслядоўнасці (х_і), і ад 1 да ∞ х_і ТП (х,τ) назыв. яе эл-т хЄХ, для любога ω_α(х),αЄІ існуе N_αЄN,так,што усе элементы дадзенай пасляд. э нумарамі >=N_αЄ ω_α(х). Калі (х_і), і ад 1 ∞ мае lim х,то яна зыходзіцца да х.

Тэарэма. Любая бясконцая паслядоўнасць элементаў хаўзд.пр-ры мае не больш за адзін lim.

Д-з. Няхай Існуе (х_і), і ад 1 да бясконцасці у ХП мае 2 lim, а і b, а≠b. lim х_і=a,

lim х_і=b, і→∞( а≠b), ω(a) перасячэнне ω(b) = пустое мноства. Па азн. ліміту усе пункты х_Nα, х_Nα+1,... Є ω(a), а х_Nβ, х_Nβ+1,... Є ω(b). Відавочна, калі N=max(N_α, N_β)=> х_N, х_Nz+1,... Є ω(a) перасячэнне ω(b) = пустое мноства. ?!

23^*.Суадносіны паміж классамі прасторау розных тыпау аддзельнасці.

Сцв.1 Усякая Т2 прастора (хаусдорфава ) ёсць Т1 прастора.

Відавочна, калі выконваецца Т2, тады выконваецца і аксіёмы Т1.

Сцв. 2 метрычная прастора ёсць нармальная прастора(Т1+Т4)

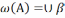
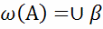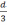
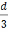Доказ. 1) метрычная праст. – хаусдорф., таму на па сцв.1 , яна Т1 пр-ра; 2) Няхай А,В – замк-ныя неперасяк. падмн-вы пр-ры (Х,т), тады мн-вы (a_α, ) і 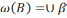(a_β, ) , дзе d –адлегласць паміж А і В. Відавочна, w(А) і w(В) з”яул. неперасяк. наваколлямі мн-вау А і В адпаведна.

Сцв.3. Нарманая пр-ра есць рэгулярная пр-ра (Т1+Т4Т1+Т3).

Доказ: 1) Т1 выконваецца; 2) няхай F- адвольнае замк-нае у пр-ры (Х,т) мн-ва і х належыць Х, і х не належыць F. Па аксіеме Т1:{x}⋴φ_x. Таму па аксіеме Т4 замк. Мн-вы F і {x} маюць неперасяк. наваколлі w(F) і w({x}) адпаведна. Таму w({x})=w(x) , значыць мае месца Т3.

Сцв.4. Рэгулярная пр-ра з”яул. хаусдорфавай (Т1+Т3=Т2).

Доказ. Няхай x,y-адвольныя пункты рэгулярнай пр-ры (Х,т). разгледзім замест Х пару: х,{y}. Па Т1 {y}⋴φ_x. Таму па Т3, існуюць неперасяк. наваколлі w(x) і w(y). **

Тапалаг. пр-ра наз. метрызавальнай,калі на мн-ве Х можна задаць такую метрыку р , што параджальная ею на мн-ве Х натуральная тапалогія тр супадае з пр-рай т.

Вядома , што калі існуе метрыка, якая параджае тапалогію пр-ры, такая метрыка , увогуле кажучы, не адзіная,

Азн. Метрыкі, зададзеныя на адным і тымжа мн-ве , якія параджаюць адну і туюж тапалогію на ім наз. эквів.

Прыклады.

1) Тапалаг. пр-ра R² метрызуецца стандарт. метрыкай р, а таксама эквів. ёй метрыкамі .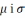

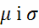2. дыскэтная тапалаг. пр-ра (Х,т*) метрызуецца дыскрэтнай метрыкай.

Тэарэма. \1-ая метрызацыйная тэар. Урысона\.Тапал. пр-ра са зліч-най базай з”яуляецца метрызальнай т. і т.т, калі яна з”яуляецца нармальнай.

26 Уласцівасці звязных прастораў і мностваў.

Тэарэма 1Калі Х- звязная пр-ра, а адлюстраванне f: X→Y непарыўная сюр’екцыя, тады пр-ра У есць звязная пр-ра. (Непарыўны вобраз звязнай пр-ры есць звязная пр-ра).

Доказ:

Прадпаложым працілеглае, г.зн, што У нязвязная пр-ра, тады У=V1 U V2 / V1,V2≠Ø,

V1, V2€ £x , V1∩V2=Ø. U1= fֿֿ ¹(V1) , U2=f ֿ¹ (V2), тады мае месца прадстаўленне Х=U1 U U2, акрамя таго U1 ,U2 € £x , U1 , U2 ≠ Ø, U1 ∩ U2 =Ø => X- звязная пр-ра, што супярэчыць прадпалажэнню.

Тэарэма 1’ (для мностваў)

Калі f: X→Y непарыўнае адлюстраванне пр-ры Х у пр-ру У, А- звязнае падмн-ва пр-ры Х, тады f(A)- звязнае подмн-ва пр-ры У.

Тэарэма 2.Замыканне звязнага мн-ва есць звязнае мн-ва.

Тэарэма 3.Аб’яднанне ўсякай сям’і звязных пр-раў, якія маюць прынамсе адзін агульны пункт есць звязная пр-ра.

Тэарэма 4.Няхай Х- звязнае пр-ра і f: X→R¹ - непарыўная лікавая функцыя, якая мае прынамсе адно дадатнае і адно адмоўнае значэнне. Тады існуе пункт х з Х такі, што f(x)=0.