18.База тапалогіі.

Базай тапал. пр-ры (Х,τ) наз. сям’я β адкрытых у пр-ры мн-ваў, калі кожнае адкрытае ў ёй мн-ва U можна прадставіць як аб’яднанне некаторай сукупнасці мн-ваў з β.

Мн-вы,якія ўваходзяць у склад базы β назю элементарнымі адкрытымі мн-вамі.

Прасцейшыя вынікі з азн. базы:

1)β⊂τ;

2)сама тапалогія τ з’яўляецца базай;

3) ⊂β;

4)калі да базы β,якая адрозніваецца ад ,дадаць прынамсі адно адкрытае ў пр-ры мн-ва атрымаем новую базу;

5)канцоўная пр-ра можа мець канц. кол-сць баз.Бясконцая пр-ра можа мець бясконцую кол-сць баз.

База β наз. мінімальнай, калі выключаючы з яе хаця бы адно мн-ва атрымаем сукупнасць,якая не з’яўляецца базай.Мн-вы, якія ўваходзяць у склад базы наз. яе элементамі.

Прыклад.Абстрактная антыдыскрэтная пр-ра (Х,τ₀),τ₀={ ,X},мае адзіную базу β={ ,X}.

Вагай тапалаг.пр-ры (Х,τ) наз. кол-сць(магутнасць мн-ва) элементаў яе мін. базы.Напрыклад,вага антыдыскрэтнай пр-ры (Х,τ₀)-2.

19. Другая аксіёма злічоннасці.

Кажуць, што тапалагічная прастора задавальняе другой аксіёме злічоннасці, калі яна валодае базай, якая складаецца з канечнай ці злічонай колькасці інварыянтаў.

Сцв.1. Уласцівасць прасторы задавальняюць другой аксіёме злічонасці ёсць тапалагічная ўласцівасць (таму што яна фармулюецца выключна ў тэрмінах адкрытых мностваў, якія пераходзяць у адкрытыя мноствы пры гамеаморфных пераўтварэннях).

Заўвага 1. Прасторы, якія задавальняюць другой аксіёме злічонасці, называюць яшчэ прасторай са злічонай базай.

Прыклад 1. Прастора 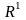задавальняе другой аксіёме злічонасці. На самай справе, яна мае злічоную базу 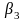, якая складаецца з усіх канечных інтэрвалаў з рацыянальнымі канцамі. Аналагічна, прасторы 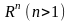таксама маюць злічоныя базы. Узнікае пытанне: ці ўсякая метрычная прастора валодае злічонай базай? Адказ: не.

Заўвага 2. Аказваецца, усякая прастора са злічонай базай з’яўляецца сепарабельнай.

Але для метрычных прастораў мае месца і адваротнае.

Тэарэма1. Метрычная прастора задавальняе другой аксіёме злічонасці тады і толькі іады, калі яна з’яўляецца сепарабельнай.

Вынік. прасторы 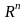– сепарабельныя.

20 Аксіемы аддзельнасці

Т1: кожны з двух пунктаў тапалагічнай прасторы мае наваколле, якое не змячае іншае.

Т2: кожныя два пункты прасторы маюць неперасякальныя наваколлі

Т3: для кожнага замкнутага ў прасторы мноства і пункта. Які не належыць гэтаму мноству, існуюць іх неперасякальныя наваколлі

Наваколлем падмноства А ТП (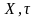 ) называюць адвольнае адкрытае ў прасторы мноства 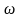(А), якое уключае мноства А.

Т 4: кожныя 2 неперасякальныя замкнутыя ў прасторы мноствы маюць неперасякальныя наваколлі

Т1 Т2 Т3 Т4

Пратора, якая задавальняе аксіеме аддзельнасці , называецца -прасторай.

Прастора, якая задавльняе Т1 і Т3 называецца рэгулярнай, прастора, якая задавальняе Т1 і Т4 называецца нармальнай. Сцв. Уласцівасці прастораў быць -прасторамі, рэгулярнай, нармальнай прасторамі з`яўляюцца тапалагічнымі.

21. Хаусдорфавыя прасторы.

Прасторы называюцца хауздорфавымі.( : Кожныя два пункты прасторы маюць неперасякальныя наваколлі.)

Тапалагічная прастора 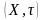называецца хауздорфавай, калі кожныя два яе нункты 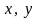маюць неперасякальныя наваколлі 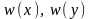адпаведна.

Прыклад1. Антыдыскрэтная прастора 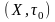– не хауздорфавая (Доказ: так як ).

Прыклад 2. Неаднаэлементная дыскрэтная прастора 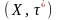– хауздорфавая (Доказ: на самай справе, ).

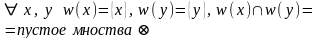Прыклад 3. Кожная неаднаэлементная метрычная прастора ёсць хауздорфавая (Доказ: на самай справе,

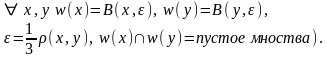
Прасцейшыя ўласцівасці хаўздорфавых прастор.

Сцв.1(Замкнутасць пункту). Кожнае аднаэлементнае падмноства хаўздорфавай прасторы – замкнутае у ёй.

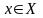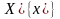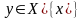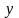Доказ сцв.1: Няхай – хаўздорфавая прастора, . Пакажам, што – адкрытае ў гэтай прасторы. Для кожнага пункту і пункта існуюць неперасякальныя наваколлі: . Такім чынам, – унутраны пункт мноства . Улічваючы адвольнасць выбранага пункта у мностве маем:

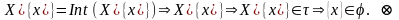
Вынік. У хаўздорфавай прасторы ўсякае канечнае мноства замкнутае (таму што аб’яднанне канечнай колькасці замкнутых мностваў - замкнутае).

Заўвага. Калі тапалагічная ўласцівасць прасторы мае месца для кожнай яе падпрасторы, то яна называецца спадчыннай . Такім чынам, хауздорфавасць ёсць спадчынная ўласцівасць прастораў. Відавочна, уласцівасць злічонасці базаў таксама спадчынная ўласцівасць, сепарабельнасць – спадчынная ўласцівасць; а вось звязнасць , лінейная звязнасць, кампактнасць – не спадчынныя ўласцівасці.