
- •2. Шары і сферы метр. Прасторы. Абмежаваныя мн-вы.
- •3.Індуцыраваная метрыка . Падпрастора метрычнай прасторы
- •5. Паняцце тапалагічнай прасторы
- •6. Замкнутыя мноствы у тапалагічнай прасторы.
- •7.Індуцыраваная тапалогія . Падпрастора тапалагічнай прасторы
- •8. Пункты дакранання і вонкавыя пункты мноства.
- •11*. Замыканне мн-ва і замкнутае мн-ва. Унутраннасць мн-ва і адкрытае мн-ва.
- •13. Непарыўныя адлюстраванні
- •14. Гамеаморфныя адлюстраванні.
- •16.Тапалагічныя уласцівасці і інварыянты.Паняцце аб прадмеце тапалогіі.
- •18.База тапалогіі.
- •20 Аксіемы аддзельнасці
- •22*. Ліміт паслядоунасці элементаў тп.
- •26 Уласцівасці звязных прастораў і мностваў.
- •30. Звязнасць і лінейная звязнасць.
- •31 И 32.Кампактныя пр-ры і мн-вы.
- •33*.Кампактнасць і замкнутасць.
- •35.Кампактныя мн-вы у эўклідавых пр-рах.
- •36.Уласцівасці камп. Пр-раў і мн-ваў.
- •37*. Прамы здабытак прастораў.
- •39. Тапалагiчныя ўласцiвасцi здабыткаў прастораў
- •40.Фактар-тапалогія, спароджанная дачыненнем эквівалентнасці.
- •41*Фактар-прасторы квадрата
30. Звязнасць і лінейная звязнасць.
Тэарэма. Любая лінейна-звязная прастора (х,τ) есць звязная прастора.
Д-з. Х=аб’яднанне (хЄХ) Sx([0,1]),дзе Sx:([0,1]) →Х, якая злучае нейкі фіксаваны пункт х0 і х, х0,хЄХ. Любое мн-ва Sx([0,1]) есць звяз.падмноства Х, яе непарыўны вобраз звязн. адрэзка [0,1] у R1(па Т.1) => Х зв. мн-ва, як аб’яднанне звязных мностваў, якія маюць агульны пункт.
Заувага1. Звязная пр-ра не абавязкова з’яўляецца лінейна-звязнай.
Вынік. Клас лінейна-звязных прастораў есць уласны падклас класа звязных прастораў.
Заувага 2. Замыканне лін-звязнага мноства не абавязкова лінейна-звязнае мноства.
Заувага 3. Магутнасць мноства камп. звязнай прасторы як і кампан. яе лін-зв.есць тапалагічны інварыянт.
Заувага 4.Не блытаць паняцці звяз. пр-ры, лін-звяз. і адназвязн.
Азн. Адназвязнай назыв. пр-ра(мн-ва) у якой(якім) любы замкнуты контур гаматопны 0.
31 И 32.Кампактныя пр-ры і мн-вы.
Азн. Адкр-м пакрыццем тапалаг. пр-ры (Х,т) наз. адвольная сукупнасць адкр-х у ей мн-вау,аб”яднанне якіх супадае з носьбітам пр-ры.
Азн.2. Тапалаг. пр-ра (Х,т) наз. кампактнай калі з усякага адкр-га яе пакрыцця можна выдяліць яе канечнае адкрытае пакрыцце, у гэтай сітуацыі апошняе наз. падпакрыццем.
Сцв.1. Уласців-ць пр-ры быць кампактнай есць яе тапалаг. ул-ць.
Напрыклад, адвольная канцоуная пр-ра (Х,т) не кампактная таму што у ей канечная кол-ць розных подмн-вау , менавіта два у ступені n, дзе n- кол-ць элементау.
Азн. Падмн-ва А тапалаг. пр-ры (Х,т) наз. кампактным у ей, калі падпр-ра (А,т~) з”яул. кампактнай пр-рай.
Азн. Адкр-ым пакрыццем падмн-ва А пр-ры (Х,т) наз. сукупнасць мн-вау , адкр-х у пр-ры (Х,т) , аб”яднанне якіх змяшчае мн-ва А.
Будем
абазн. праз 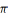
 A={Vβ׀Vβ
A={Vβ׀Vβ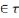
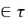 x,β
x,β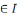
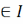 }
}
Сцв.2. \крытэрый кампактнасці мн-ва у пр-ры\ . Падмн-ва А пр-ры (Х,т) з”яул. кампактным у ей т. і т. т.,калі з кожнага адкр. пакрыцця №№ мн-ва А можна выдяліць яе канечнае пакрыцце.
Напрыклад, адрэзак [0,1] – кампактнае у R мн-ва.
Заув. Уласцівасць кампактнасці – не спадчынная уласцівасць.
33*.Кампактнасць і замкнутасць.
Тэарэма
1.Няхай
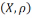 -кампактная
прастора, калі
-кампактная
прастора, калі 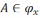 ,
тады А кампактнае ў ёй мноства
,
тады А кампактнае ў ёй мноства
Д
оказ. 1) Няхай
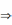 X\
A
X\
A
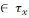 ;
;
Х
А

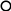 2)
2)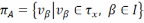 ;
;
А
Х
3)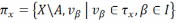 -- ёсць
адкрытае пакрыццё прасторы X.
-- ёсць
адкрытае пакрыццё прасторы X.
4)Паколькі -кампактная прастора, з яго можна выбраць канечнае падпакрыццё прасторы X

 =
=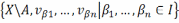

5)Тады
сукупнасць 
 будзе,
відавочна, канечным падпакрыццём мноства
A,
якое выдзелена з яго адвольным пакрыццём
будзе,
відавочна, канечным падпакрыццём мноства
A,
якое выдзелена з яго адвольным пакрыццём
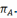
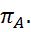
Такім чынам A па крытэрыю ёсць кампактнае мноства у прасторы.
Тэарэма
2.Няхай
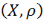 -- хаўздорфава прастора. Калі A—кампактнае
яе падмноства, тады A
замкнутае ў ёй падмноства.
-- хаўздорфава прастора. Калі A—кампактнае
яе падмноства, тады A
замкнутае ў ёй падмноства.
Тапалагічныя прасторы, якія з’яўляюцца адначасова кампактнымі і хаўздорфавымі, назыв. кампактамі.
Тэарэма
3.Няхай
 —кампакт.Падмноства
A
камп. у ім тады і толькі тады, калі яно
замкнутае.
—кампакт.Падмноства
A
камп. у ім тады і толькі тады, калі яно
замкнутае.
34*.

Тэарэма
1. Няхай
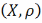 – метрычная прастора. Калі А яе кампактнае
падмонства, тады А – замкнутае і
абмежаванае.
– метрычная прастора. Калі А яе кампактнае
падмонства, тады А – замкнутае і
абмежаванае.
Доказ.
1) Паколькі метрычная прастора з’ яўляецца хауздорфавай, то замкнутае яе кампактнае падмноства вынікае з тэарэмы, што калі -- хауздорфава прастора, А – кампактнае яе падмноства, тады А – замкнутае ў ёй падмноства.
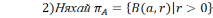
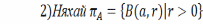 ,
a=const
– сукупнасць канцэнтраваных адкрытых
шароў з цэнтрам у пункце a
,
a=const
– сукупнасць канцэнтраваных адкрытых
шароў з цэнтрам у пункце a A.
A.
Паколькі
А—кампактнае мноства, з яго пакрыццём
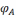 ,
можна выбраць канечнае падпакрыццё
,
можна выбраць канечнае падпакрыццё
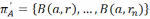
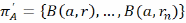 ,
тады, відавочна, мноства А будзе падмноства
,
тады, відавочна, мноства А будзе падмноства
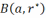
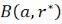 ,
,

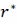 =max
=max
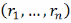 .
.
Значыць
А – абмежаванае мноства ў прасторы
 .
.
