39. Тапалагiчныя ўласцiвасцi здабыткаў прастораў

Тэарэма1Здабытак канечнай цi злiчонай колькасцi прастораў,якiя задавальняюць другой аксiёме злiчонасцi ёсць прастора,якая задавальняюць другой аксiёме злiчонасцi, гэта значыць мае злiчоную базу.

Тэарэма2 Здабытак хаусдорфавых (Т₁,рэгулярных) прастораў ёсць хаусдорфавая (Т₁,рэгулярная) прастора.

Заўвага Адпаведнае сцверджанне для нармальных прастор не мае месца.

Тэарэма3 Здабытак звязных прастораў ёсць звязная прастора.

Тэарэма4 (Цiханава) Здабытак кампактных прастораў ёсць кам-пактная прастора.

Доказ:

Тэарэма 2 для здабытака двух прастор. Няхай Х,У- хаусдорфавыя прасторы. Пакажам, што ix здабытак Х У хаусдорфавая прастора.

Возьмем два пункта (х₁,у₁),(х₂,у₂).

1) х₁≠х₂, паколькi Х- хаусдорфавая прастора неперасякальныя наваколлi ω(х₁),ω(х₂) пунктаў х₁,х₂ у Х. Тады мноствы ёсць неперасякальныя наваколлi пунктаў (х₁,у₁),(х₂,у₂) у прасторы Х У. На самай справе гэтыя мноствы адкрытыя у Х У i першае з iх змяшчае пункт (х₁,у₁), а другое - пункт (х₂,у₂) i неперасякаль-ныя.

2)калi х₁=х₂ ,тады у₁≠у₂ i ў якасцi неперасякальных навакол-ляў пунктаў (х₁,у₁),(х₂,у₂) можна ўзяць вiдавочна мноствы ω((х₁,у₁))=Х ω(у₁), ω((х₂,у₂))=Х ω(у₂), дзе ω(у₁), ω(у₂) неперася-кальныя наваколлi пунктаў у₁,у₂ у хаусдорфавай прасторы У.

№37 Фактар-тапалогія, спароджанная сюр’ектыўным адлюстраваннем.

Няхай f-сюр’екцыйнае адлюстраванне тапалагічнай пр-ры (Х, τ_х ) на мн-ва У.

Фактар-тапалогіяй на мн-ве У, спароджаннай сюр’екцыяй f называецца сукупнасць (τ_f)_y падмностваў мн-ва У, правобразы якіх пры адлюстраванні f есць адкрытае мн-ва ў пр-ры (Х, τ_х ).

Сцв.1Фактар-тапалогія (τ_f)_y есць тапалогія на У.

Калі на мн-ве У уведзена фактар-тапалогія (τ_f)_y атрымоўваем тапалагічную пр-ру (У,(τ_f)_y) якая наз. Фактар-тапалогіяй спароджаннай сюр’екцыяй f. Сюрхекцыя f наз. Фактар-адлюстраванне.

Сцв.2Фактар-адлюстраванне f: (Х, τ_x ) на → (У, (τ_x)_y) – непарыўнае адлюстраванне.

40.Фактар-тапалогія, спароджанная дачыненнем эквівалентнасці.

Няхай ~ - бінарнае дачыненне эквівалентнасці на Х.Абазначым праз [x] – сукупнасць усіх элементаў мн-ваў Х эквівалентных элементу х , [x]={y€X / x~y}.

Заувага.Відавочна, калі х1~х2 => [x1]=[x2]. [x]- клас эквівалентнасці элемента х.

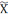
Мн-ва 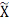, элементамі якога з’яўляюцца ўсе класы эквівалентнасці мн-ва Х па зададзеннаму у ім дачыненню эквівалентнасці~ наз фактар-мноствам.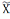 ={[x]/ x€X}.

ЗаувагаЧасам дачыненне эквівалентнасці на мн-ве Х Абазначаецца вялікай літарай напр R.

41*Фактар-прасторы квадрата

1) Няхай K={(x,y)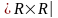 x [0;1],y [0;1]} – адзінкавы квадрат на плоскасці. Будзем яго разглядаць з тапалогіяй , індуцыраваннай на ім тапалогіяй прасторы . Зададзім на К дачыненне эквівалентнасці 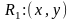~R(x,y), калі x (0;1),y [0;1]. (0,y)~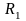 (1,y), калі y [0;1]. Пункты верцікальных бакоў квадрата эквівалентныя тады і толькі тады, калі маюць аднолькавыя ардынаты, кожны з астатніх яго пунктў эквівалентны сабе. Фактар-мноства R/ графічна прадстаўляюць у выглядзе (мал1). Гэты малюнак называюць фактар-дыяграмай фактар-мноства R/ . Адпаведнае адлюстраванне 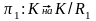; 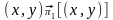графічна паказваюць мал2. Стрэлкі на верцікальных баках накіраваныя ў адзін бок і паказваюць, што адпаведныя пункты гэтых бакоў (якія маюць аднолькавыя ардынаты) склеіваюцца. Калі на К уведзена індуцыраванная тапалогія , адпаведная фактар-прастора 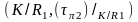гамеаморфна цыліндру у , а іменна прасторы 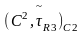. Рысаваць мал1 ~ цыліндр. Прастора называецца тапалагічным цыліндрам. 2) Зададзім наступнае дачыненне эквівалентнасці на К мал3. Аказваецца, што , Апошняя прастора называецца стужкай мебіуса. 3) Зададзім на квадраце К наступным чынам мал4. 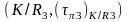~ ( ) – тапалагічная сфера. 4) Вызначым дачыненне эквівалентнасці на квадраце К наступным чынам мал5. Пункты бакоў квадрата эквівалентныя, калі яны сіметрычныя адносна сярэдняй лініі гэтага квадрата. 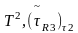~ ( ) – тапалагічны тор. 5) Зададзім 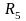на квадраце К наступным чынам мал6. ~ ( ) – бутэлька Клейна. Пры гэтым у прасторы не існуе паверхні, гамеаморфнай гэтай прасторы, але такая паверхня існуе ў 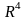. 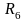6) Зададзім на квадраце К наступным чынам мал7. 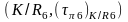~ ( 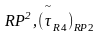) – тапалагічная праектыўная плоскасць. Пры гэтым у прасторы не існуе паверхні, гамеаморфнай гэтай прасторы, але такая паверхня існуе ў . Заўвага паколькі квадрат – кампактнае лінейна звязнае, звязнае мноства ў , а фактар-адлюстраванне непарыўнае, усе атрыманыя ў гэтым пункце прасторы з`яўляюцца кампактнымі, звязнымі, лінейна звязнымі. Можна даказаць, што яны з`яўляюцца хаўсдорфавымі і валодюць злічонай базай, паколькі апошнія тапалагічныя ўласцівасці з`яўляюцца спадчыннымі.

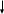
М ал1 мал2 мал3 мал4 мал5

м ал6 мал7

№24 Звязныя і нязвязныя прасторы.

Тапалагічная прастора наз.звязнай калі яе нельга прадставіць як аб’яднанне двух адкрытых у ей не пустых, не перасякальных падмноствау u i v.

Натуральна-тапалагічная прастора наз. нязвязнай , калі Яна не з’яул. Звязнай:

(

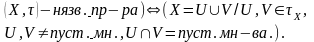
Сцв.1Уласцівасць прасторы быць звязнай(нязвязнай) есць яе тапалагічная уласціавсць.

Сцв.2 Тапалагічная прастора з’яуляецца звязнай тады і Толькі тады калі яе нельга прадставіть у выглядзе аб’яднання двух замкнутых у ей непустых неперасякальных мноствау.

Доказ

Калі (X,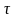 )-нязвязная прастора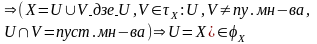

V=X\U .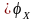

Сцв.3 Тапалагічная прстора з’яуляецца звязнай тады і Толькі тады калі у ей есць Толькі 2 адкрыта-замкнутых мноствау.

Доказ Няхай (X, )звязная пр-ра і ей есць адкрыта-замкнутае мн-ва U акрамя пуст.мн-ва,X. Тады V=X\U-адкрыта-замкнутае мн-ва.Таму будзем мець

(X=U V/ U,V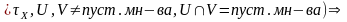 гэта зн. (X, )-нязвязная пр-ра. Што супярэчыць умове.

Прыклад Дыскрэтная прастора 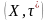у якой больш за адзін пункт –нязвязная прастора.(таму што адвольнае яе падмн-ва адкрытае і замкнутае)

25 Звязныя і нязвязныя мн-вы.

Падмноства А тапалагічнай прасторы наз. звязным у ей калі падпрастора з’яуляецца звязнай.

-індуціраваная тапалогія на А. Аналагічна уводзіцца паняцце нязвязнага мн-ва у прасторы.

_Сцв.1(А-звязнае падмн-ва тапалагічнай прасторы )

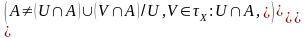
Заувага Улічваючы асацыятыунасць мн-вау,апошнюю роунасць можам перапісаць:

Прыклад Падмн-ва А антыдыскрэтнай прасторы 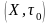з’яул. Звязнай у ей таму што падпр-ра 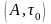з’яул. Антыдыскрэтнай прасторай.

Сцв2 падмн-ва А лікавай прамой якое змяшчае некаторыя два лікі a,b, але (a<b) не змяшчае нейкі прамежкавы пункт с (a<c<b) есць нязвязнае мн-ва у .

Доказ

U=(-∞,c) V=(c,+∞)

(A=( /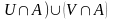

Вынік Мн-вы [0,1) [2,3],{1,3,5},N,Z,Q,I-нязвязныя мн-вы у

Заувага Звязнымі у з’яул. Наступныя мн-вы: інтэрвалы,пауінтэрвалы, адрэзкі, аднаэлементныя мн-вы, пустое мн-ва,_R.

Абсягам у пр-ры наз. адкрытае і звязнае яе падмн-ва, такім чынам (0,1)-абсяг у ,а [0,1),(0,1) (2,3) не абсягі у .

№27* Кампаненты звязнасці прасторы

Кампанентай звязнасці тапалагічнай прасторы наз. усякае яе звязнае падмн-ва, якое не змяшчаецца ні у якім іншым яе звязным падмн-ве. Патрабаванне сфарм-ае у азначэнні наз. умовай максімальнасці кампаненты звязнасці.

Сцв.1Колькасць кампанент звязнасці пр-ры есць яе тапалагічны інварыянт.

Сцв.2Усякая звязная пр-ра мае адзіную кампаненту звязнасці,якая супадае з яе нозьбітам ,паколькі Яна змяшчае усякае звязнае свае падмн-ва.

Сцв3Усякія две кампаненты звязнасці пр-ры не перасякаюцца.

Сцв4Усякі пункт x X змяшчаецца у некаторай кампаненце звязнасці гэтай пр-ры: 1) -звязнае уX

2)Калі возьмем аб’яднанне 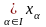усіх звязных мн-вау у пр-ры X па тэарэме3 атрымаем звязнае падмн-ва X, якое здавальняе умове максімальнасці і такім чынам з’яул. Кампанентай звязнасці, якая змяшчае x.

Сцв5 усякая тап. пр-ра X есць аб’яднанне усіх сваіх папарна неперасяк. Кампанент звязнасці :

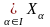X= ,

Сцв6 Усякая кампанента звязнасці пр-ры есць замкнутае у ей мн-ва.

Доказ Няхай С- камп-та звязнасці пр-ры X,тады 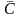-звязнае у X мн-ва.

Паколькі С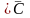 , а С-максімальнае звязнае падмн-ва X маем С= С .

Сцв7Калі пр-ра X мае канцоуную колькасць кампанент звязнасці ,тады кожнае з іх есць адкрытае у гэтай пр-ры мн-ва.

Доказ З умовы вынікае , што X=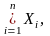 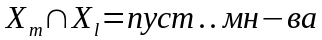, калі m l. Адсюль будзем мець

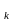X =X \ ( ) .

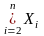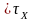Сцв8Калі пр-ра мае канцоуную колькасць кампанент звязнасці , тады Яны адначасова адкрытыя і замкнутыя у ей мн-вы.

Кампаненты звязнасці мноства

Кампанентай звязнасці падмн-ва А пр-ры наз. кампанента звязнасці яе пр-ры(А, ).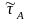

Прыклад Кожнае аднаэлементнае падмн-ва есць кампанента звязнасці мн-ва Q.

Вынік Кампаненты звязнасці мн-ва А у адносінах да падпр-ры здав-ць Сцв 1-8 .

№28 Лінейна звязныя прасторы

Шляхам у тапалагічнай пр-ры наз. адвольнае непарыунае адлюстраванне S:[0,1] X.

Пункты s(0)=a, s(1)=b наз. адпаведна пачаткам і канцом шляха s. Шлях s злучае пункты a і b.

Тапалагічная пр-ра наз. лінейна звязнай, калі адвольныя два яе пункты можна злучыць шляхам.

Сцв1. Уласцівасць пр-ры X быць лінейна звязнай есць яе тапалагічная уласцівасць.

Доказ Няхай X-лін. Звязная пр-ра ,f:X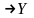 (Y=f(x)) адвольнае яе гамеаморфнае пераутварэнне.

Пакажам, што Y-лін. Звязнае. Няхай a,b I. Раздзелім правобразы f (a),f (b) пунктау a і b пры адлюстр. F Т.як X-лін. звязн. пр-ра іх можна злучыць шляхам S у пр-ры X.

S(0)=f (a), S(1)=f (b).

Пакажам, што злучае пункты a і b.

f -непарыунае адл-не

(f )(0)=f(s(0))=f(f (a))=a,

(f )(1)=f(s(1))=f(f (b))=b,

Зн. Шлях f злучае пункты a і b у Y.

Заувага Уласцівасць пр-ры быць не лінейна звязнай таксама яе тапалагічная уласцівасць.

Прыклады 1.Адвольная антыдыскрэтная пр-ра (X,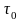 ) лінейна звязная паколькі усякае адлюстраванне у антыдыскрэтнай пр-ры непарыунае.

29Лінейна звязныя мноствы

Падмн-ва А тапалагічнай прасторы (X, ) наз. лінейна звязным у ей , калі падпр-ра(А,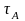 ) лінейна звязная.

Сцв1. (крытэр лінейнай звязнасці мн-вау) Падмн-ва А тапалагічнай прасторы (X, ) лінейна звязнае у ей тады і Толькі тады калі кожныя два пункты мн-ва А можна злучыць шляхам S,

Які цалкам ляжыць у А (S(t) A, t [0,1])

Прыклад 1. інтэрвалы, пауінтэрвалы , адрэзкі у

2.Адвольнае выпуклае падмн-ва лінейна звязнае.