5. Паняцце тапалагічнай прасторы

Тапалогіей на непустым мн-ве Х наз. адвольная сукупнасць τ яго падмн-ау , якая задавальняе умовам:

1) Ø, Х τ

2) аб'яднанне адвольнай колькасці мн-ау з сукупнасці τ належацьτ

3)перасячэнне канцоунай колькасці мн-ау з τ належаць τ.

Мн-ва Х на якім зафіксавана некаторая тапалогія τ наз. тапалагічнай прасторай і абазн (X, τ) . На мн-ве можна увесці шмат тапалогіяу. Калі з кантэксту зразумела якая тапалогія уведзена на мн-ве Х тапал. пр-ру могуць абазначаць Х. Эл-ты мн-ва Х наз. пунктамі тапалаг. пр-ры (Х, τ) . Мн-ва Х наз. носьбітамі гэтай пр-ры . Мн-вы, якія уваходзяць у склад тапалогіі τ наз. адкрытымі у тапалагічнай пр-ры (Х, τ)

Прыклад. Кожнай м.п. (X,p) адпавядае адзіная тапал. пр-ра (Х, τ) , дзе τ натур. тапал. м.п. (Х,p) . Гэтая пр-ра наз. спараджальнай м.п. (X,p) . Такім чынам усе м.п. уключаюцца у склад тапал. пр-ай

Прыклад.Сукупнасць τ₀={Ø,X} падмн-ва мн-ва Х наз. антыдыскрэтнай тапалогіяй на мн-ве Х . Відавочна антыдскрэтная тапалогія на Х есць тапалогія на Х .(х, τ₀)- антыдыскр. тапал. пр-ра

Прыклад. Сукупнасць τ^*=2^х – усіх пад-ваў мн-ва Х (уключаючы Ø) наз. дыскрэтнай тапалогіяй на мн-ве Х. Дыскрэтная тапалогія на Х есць тапалогія на Х . Адпаведна (Х, τ^*) наз. дыскр. тапалаг . пр-рай

Сцв. Для адвольнай іншай тапалогіі τ на мн-ве Х мае месца уключэнне τ₀ ⊂ τ⊂ τ^* .

Параўнанне тапалогіі.Калі τ₁, τ₂-тапалогіі на мн-ве Х, τ₁⊂ τ₂, τ₁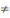 τ₂ кажуць, што тапалогія τ₁ слабейшая за тапалогію τ₂, а тапалогія τ₂ мацнейшая. Калі τ₁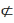 τ₂ і τ₂⊄τ₁, то τ₁ і τ₂ наз. непараўнальнымі.

6. Замкнутыя мноствы у тапалагічнай прасторы.

Падмн-ва F тапалаг. пр-ры (Х,p) наз. замкнутай у яе, калі мн-ва С_xF= X\F есць адкрытае у гэтай пр-ры мн-ва.Сукупнасць усіх замкн. мн-ваў у пр-ры (Х,p) абазн. праз .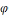 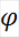_х

Сцв. Мн-ва А τ_x X\А Є 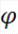_x

Азн. Мн-ва адначасова адкрытае і замкнутае у пр-ры наз. адкрыта-замк. у ей

Тэарэма.1 Усякае адкрытае у R¹ мн-ва есць аб’яднанне не больш, чым злічонай колькасці папарна неперасяк. інтэрвалау.

Тэарэма 2.усякае замкнутае ў лікавай прамой мн-ва можа быць атрымана ўдаленнем з мн-ва R небольш чым злічонай кол-сці папарна не перасякальных інтэрвалаў.

Заувага. У тапал. пр-рах могуць рэалтзовацца усе магцымыя варыянты сувязі паміж уласц-мі адкрытасці і замкнутасці мн-ва:

1. мн-ва можа быць адначасова адкрытым і замкнутым , напрыклад Ø ,Х у кожным тапал. пр-ры (Х, τ), ці кожнае падмн-ва дыскр. пр-ры (Х, τ^*)

2. Мн-ва можа быць адкрытым, але не замкнутым у пр-ры , напрыклад (0,1) у R' , шар B² у R² , аднаэлементнае мн-ва {0} у пр-ры ({a,b}, τ₂)

3. мн-ва можа , быць замкнутым , але адкрытым , напрыклад : [0,1] у R¹ , D² у R² , {b} у пр-ры ({a,b}, τ₁)

4. можа быць ні адкрытым, ні замкнутым , напрыклад : [0,1] у R¹ ці {a} ,{b} у мн-ве ({a,b}, τ₀).

Тэарэма Няхай 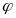сукупнасць усіх замкнутых мн-ау у пр-ры (Х,τ), тады

1) Ø і Х .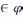

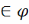2)аб'яднанне канцоун. колькасці мн-ау з φ належыць φ

3) перасячэнне адвол. мн-ау з φ належыць φ

Доказ:

1) відавочна

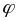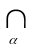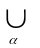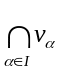2) Няхай v₁,v₂Є , Х\(v₁Uv₂) = (X\v₁) (X\v₂)Єτ . ( Тады улічваючы акс. 3 тапалогіі)маем => (па азн. замк. мн-ва ) v₁Uv₂Є . Улічваючы метад поунай мат. індукціі гэты вынік можна распаусюдзіць на адвольную канцоуную колькасць мн-вау. 3) {Vм} , αЄ I . адвол. сукупнасць мн-ау з φ.Тады маем X\( v_α)= (X\v_α) (па акс . з тапал. ) Єτ => (па азн. замк. мн-ау ) Є .⊠