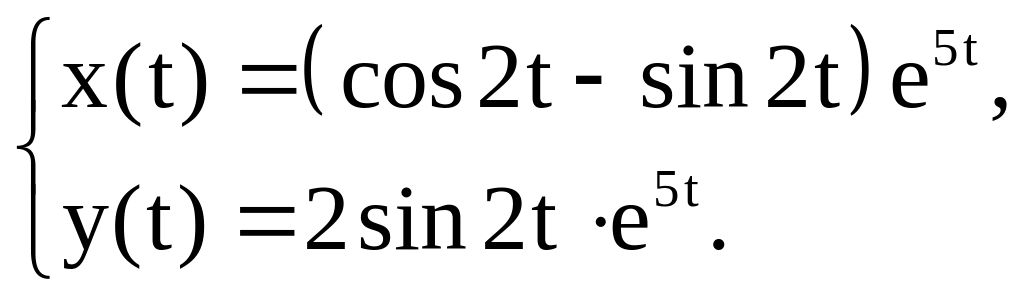- •8. Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами
- •9. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
- •10. Метод вариации постоянных
- •11. Задачи, приводящие к дифференциальным уравнениям
- •12. Системы дифференциальных уравнений. Линейные системы
- •13. Линейные однородные системы с постоянными коэффициентами
- •14. Линейные неоднородные системы дифференциальных уравнений
13. Линейные однородные системы с постоянными коэффициентами
Если
все коэффициенты
в системе (22) являются постоянными
величинами, то система (22) называется
системой с постоянными коэффициентами;
матрица
![]() является постоянной.
является постоянной.
Для нахождения фундаментальной системы решений однородной системы с постоянными коэффициентами решают характеристическое уравнение
![]() . (24)
. (24)
Набору
из n
корней (с учетом кратности)
![]() уравнения (24) ставят в соответствие
определенный набор частных решений
уравнения (24) ставят в соответствие
определенный набор частных решений
![]() ,
составляющих ФСР системы.
,
составляющих ФСР системы.
А. Если – простой корень уравнения (24), то ему ставится в соответствие вектор-функция (частное решение однородной системы)
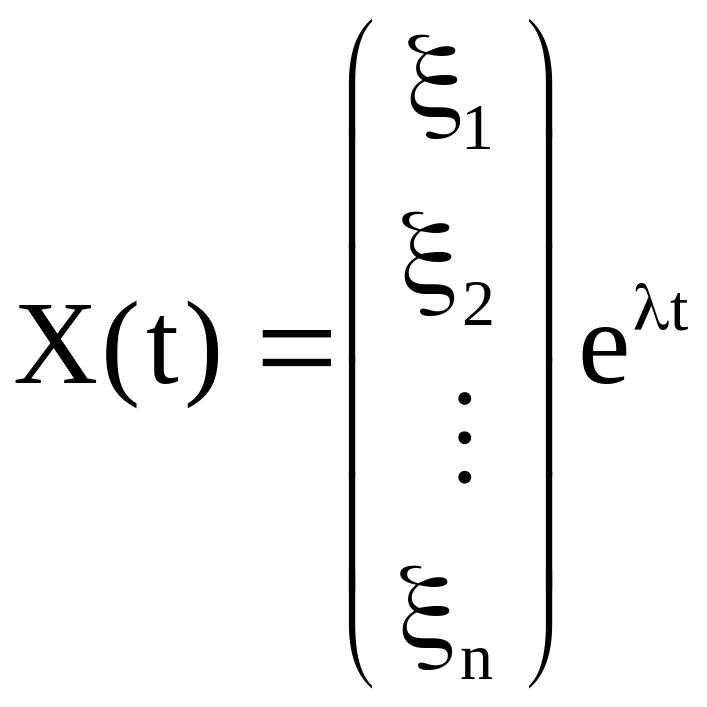 ,
,
где
![]() – собственный
вектор матрицы А, соответствующий
собственному значению .
– собственный
вектор матрицы А, соответствующий
собственному значению .
Б. Если
![]() –
простые попарно сопряженные комплексные
корни уравнения (24), то этой паре ставится
в соответствие пара функций
–
простые попарно сопряженные комплексные
корни уравнения (24), то этой паре ставится
в соответствие пара функций
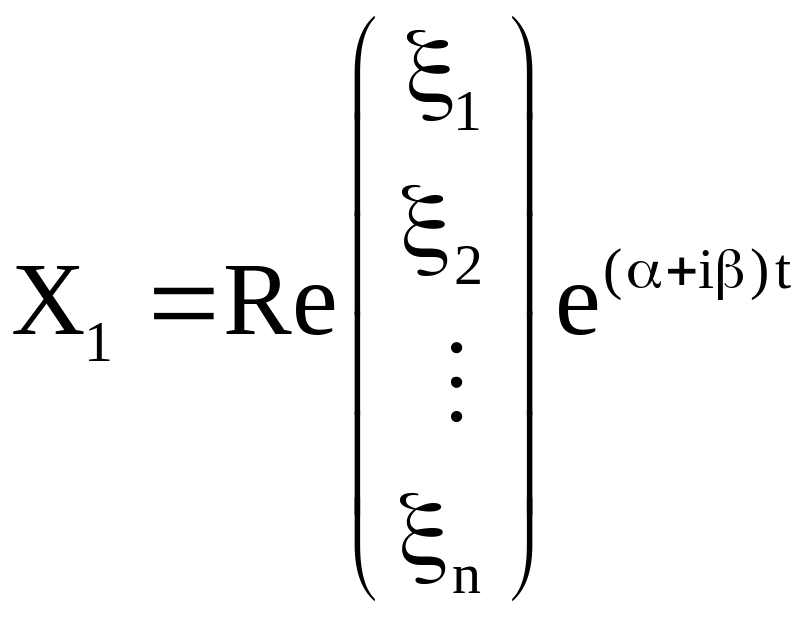 ,
,
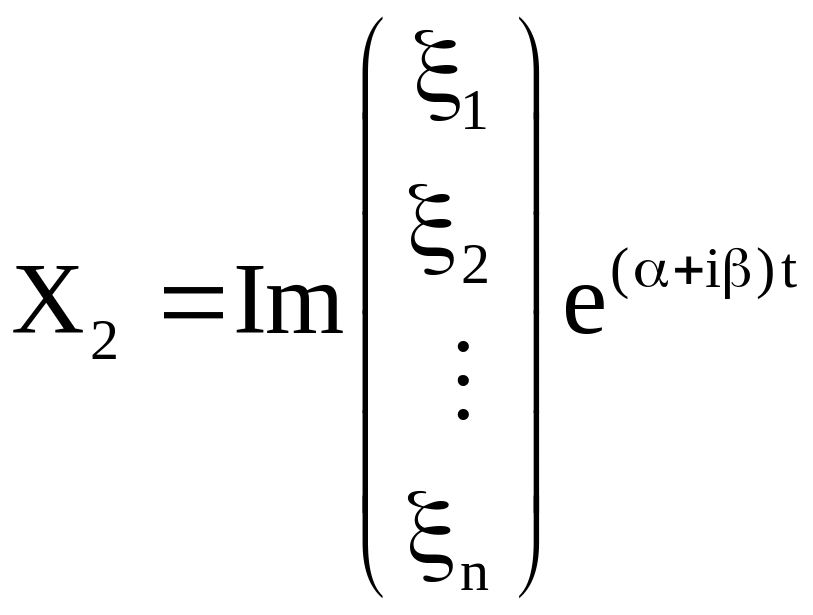 ,
,
где,
как и прежде,
–
собственный вектор матрицы А,
соответствующий собственному значению
![]() .
.
В. Если – корень кратностью r 1, то общее решение системы (22) ищется в виде
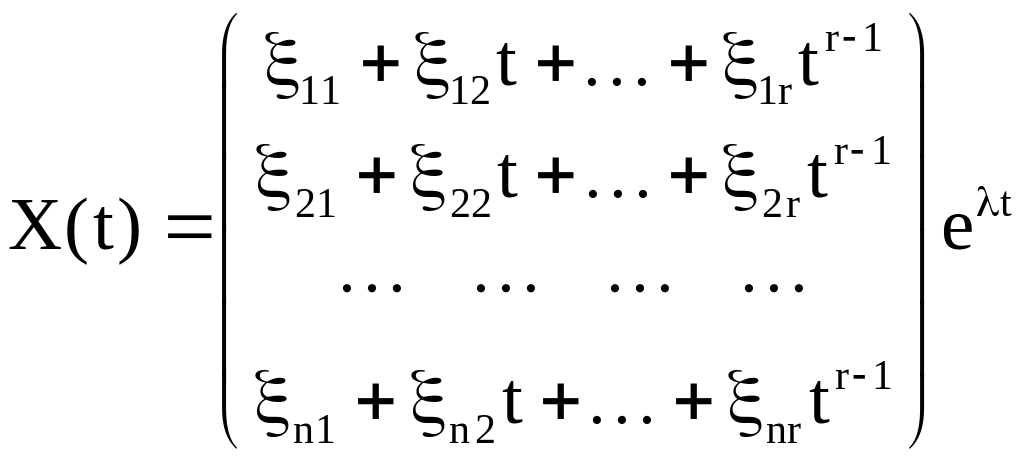 ,
,
при
этом
![]() находят путем подстановки этой функции
в систему (22).
находят путем подстановки этой функции
в систему (22).
Пример 24. Решить задачу Коши
 x(0)=3, y(0)=1.
x(0)=3, y(0)=1.
Решение. Матрица системы имеет вид
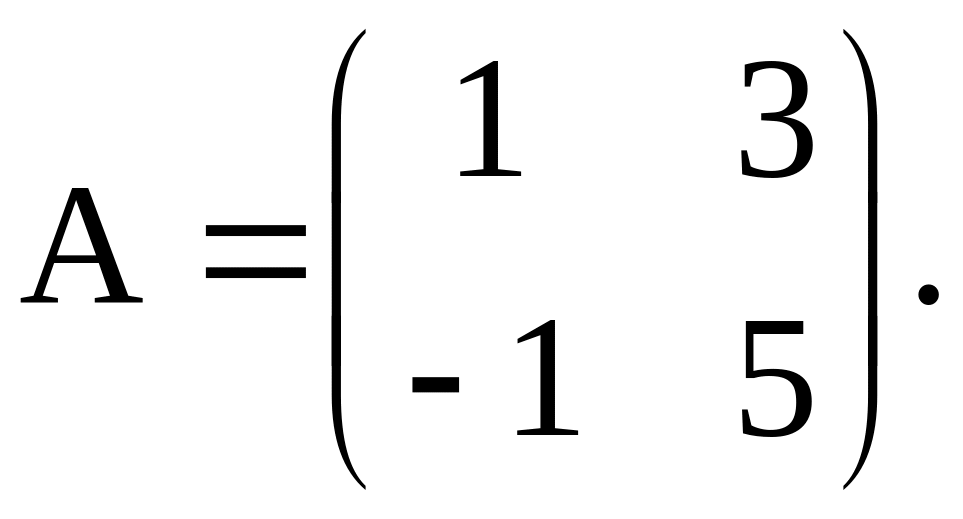
Решим характеристическое уравнение
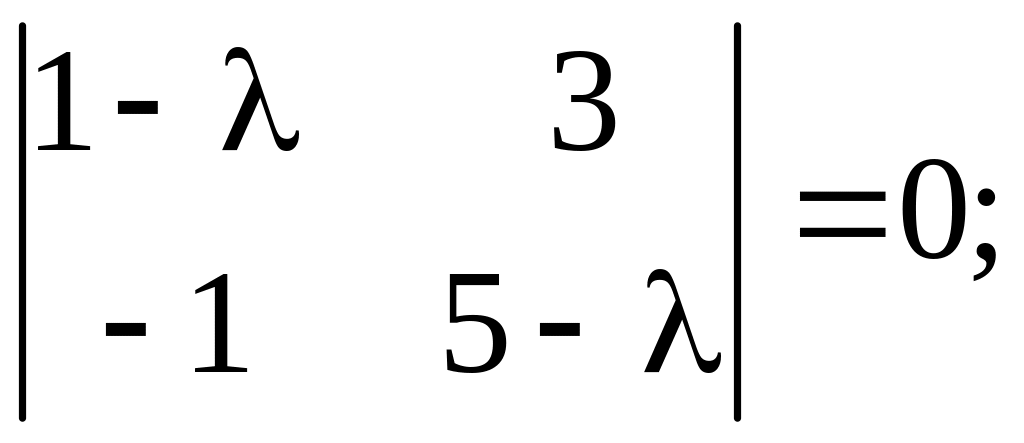
![]()
![]() – простые
корни.
– простые
корни.
Найдем собственные векторы матрицы А, соответствующие этим собственным значениям.
1) =2. Найдем собственный вектор, соответствующий .
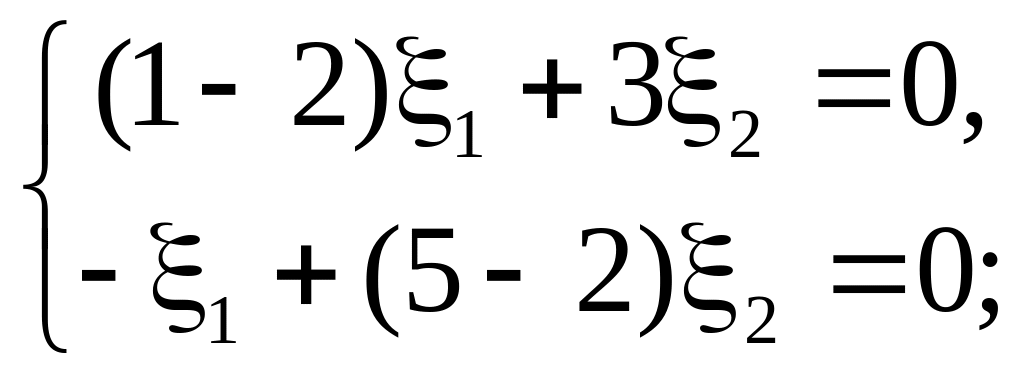
![]()
В
качестве собственного вектора можно
взять
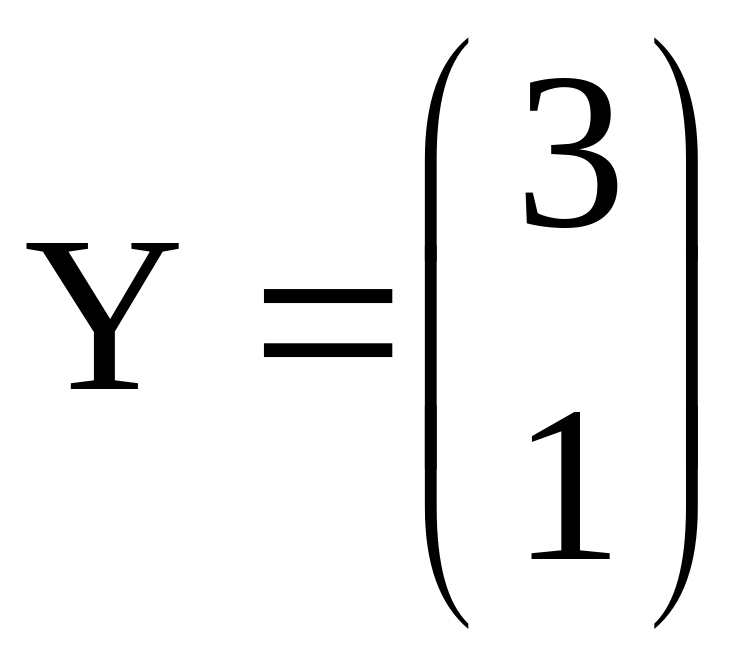 ,
следовательно,
,
следовательно,
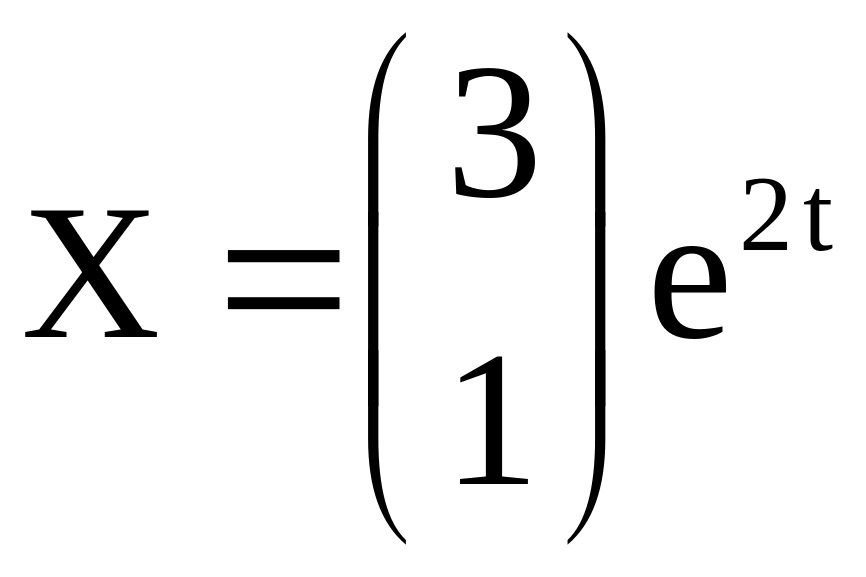 будет частным решением однородной
системы.
будет частным решением однородной
системы.
2)
![]() .
Это собственное значение приводит к
системе
.
Это собственное значение приводит к
системе
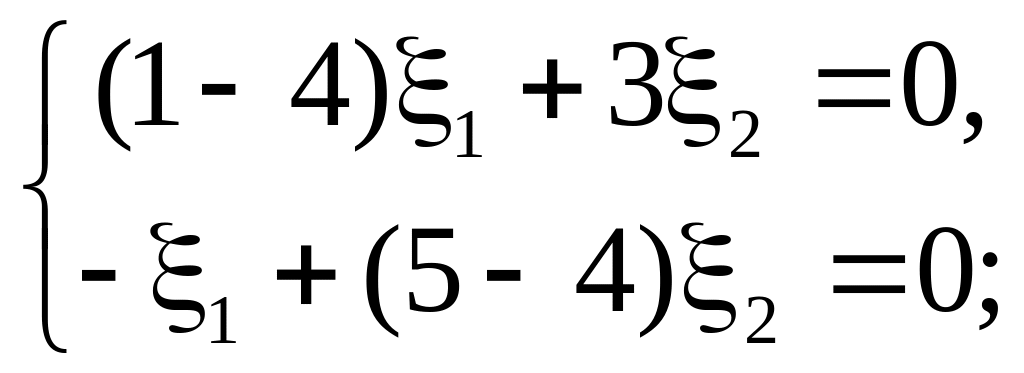
![]()
Вектор
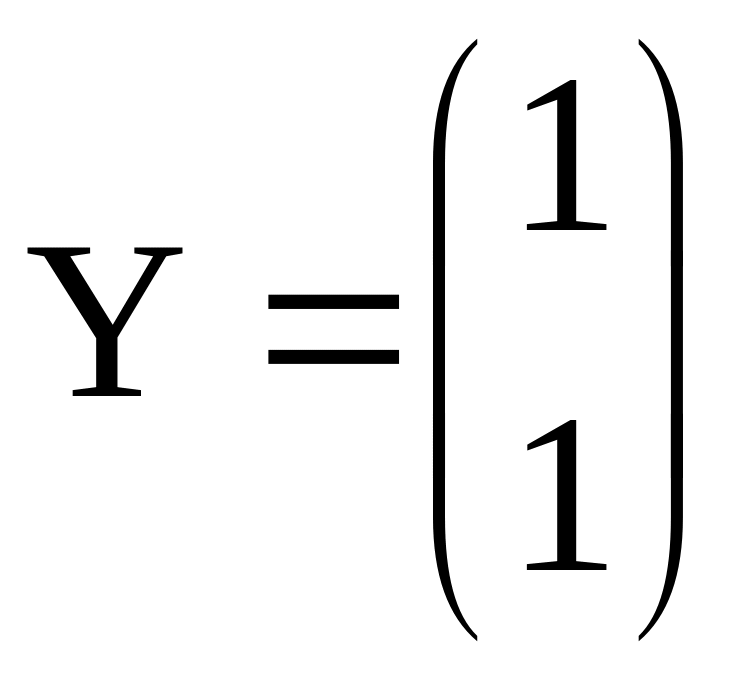 является собственным вектором, отвечающим
собственному значению
.
В качестве второго элемента ФСР однородной
системы можно взять
является собственным вектором, отвечающим
собственному значению
.
В качестве второго элемента ФСР однородной
системы можно взять
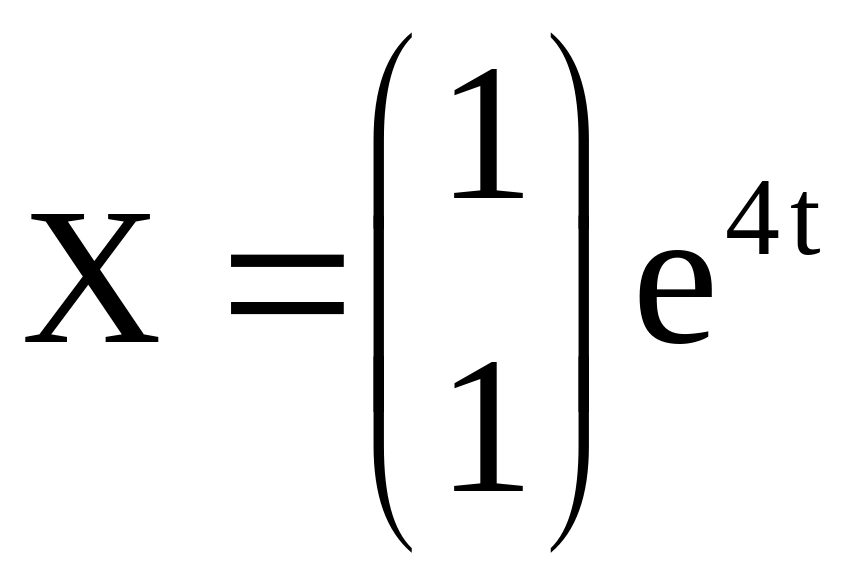 .
.
Общее решение однородной системы имеет вид
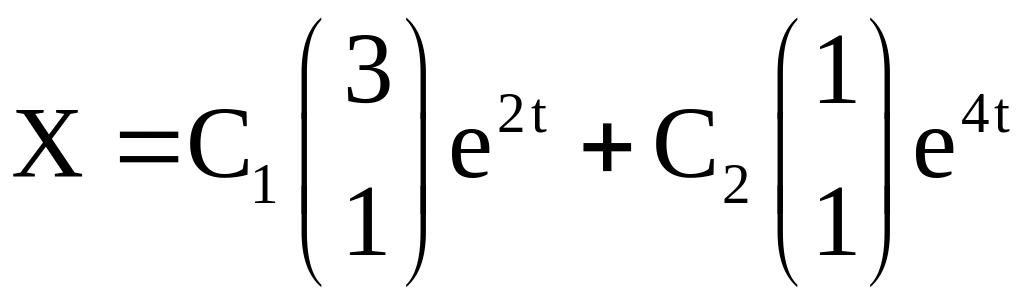 ,
,
где
![]() –
произвольные постоянные, иначе говоря,
общим решением однородной системы
является
–
произвольные постоянные, иначе говоря,
общим решением однородной системы
является

Для нахождения коэффициентов воспользуемся начальными условиями:
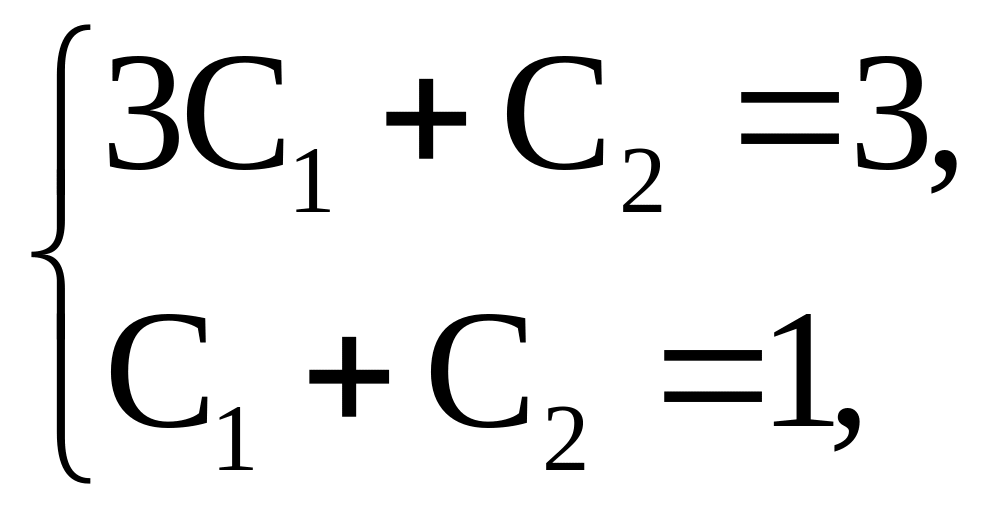
отсюда
находим
![]() .
Таким образом, решением задачи Коши
является
.
Таким образом, решением задачи Коши
является
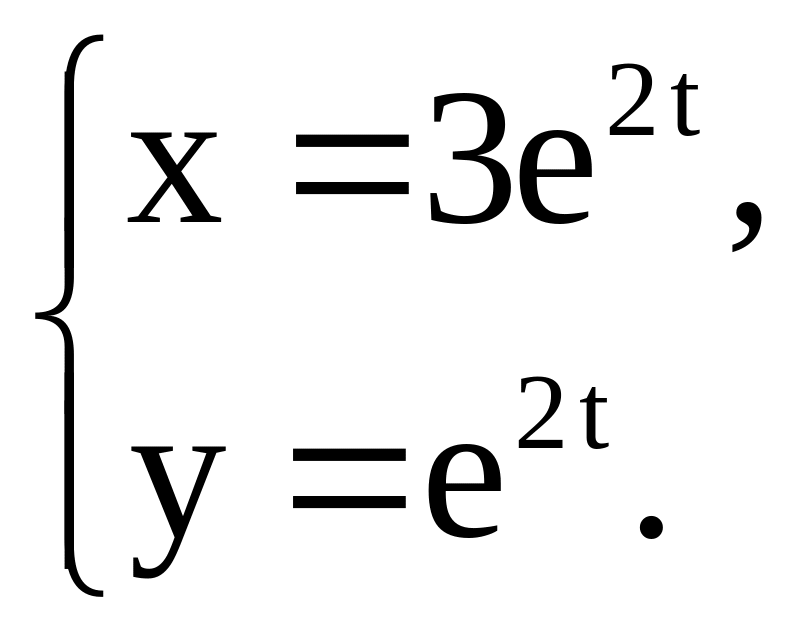
Пример 25. Решить систему дифференциальных уравнений

Решение. Матрица этой линейной однородной системы с постоянными коэффициентами имеет вид
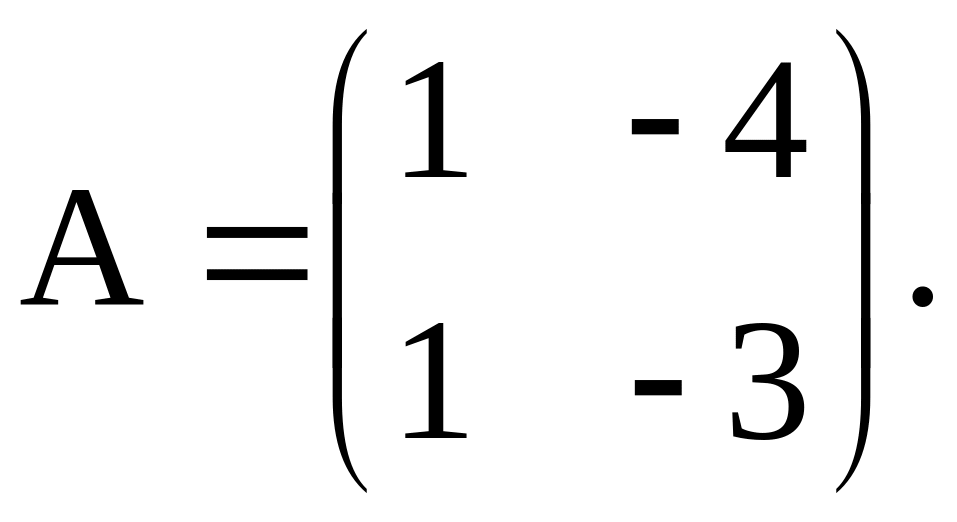
Найдем собственные значения этой матрицы:
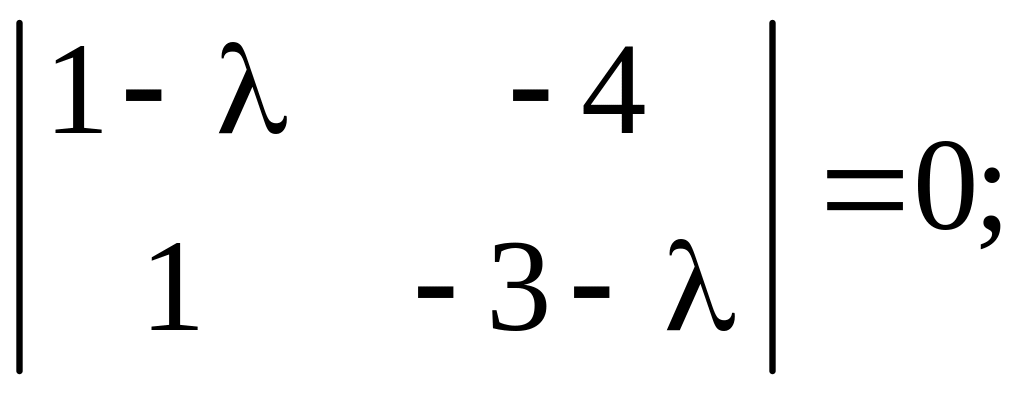
![]()
![]() –
двукратный
корень этого характеристического
уравнения.
–
двукратный
корень этого характеристического
уравнения.
Общее решение системы уравнений будем искать в виде вектор- функции
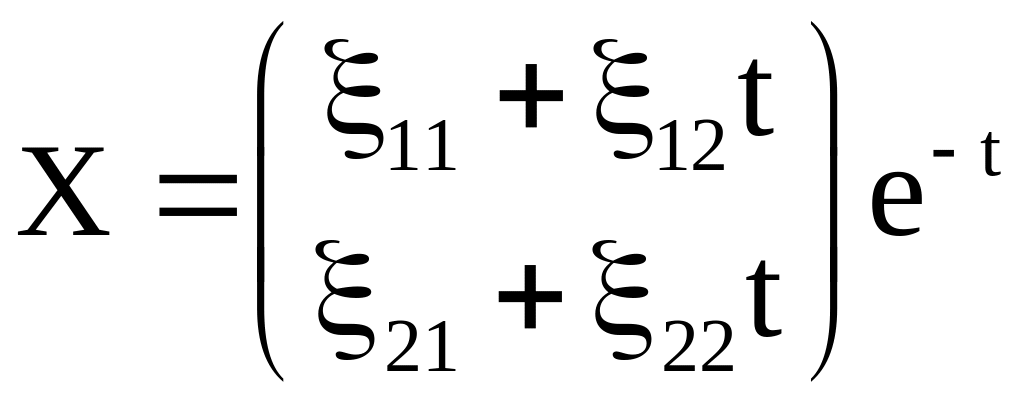 ,
,
или
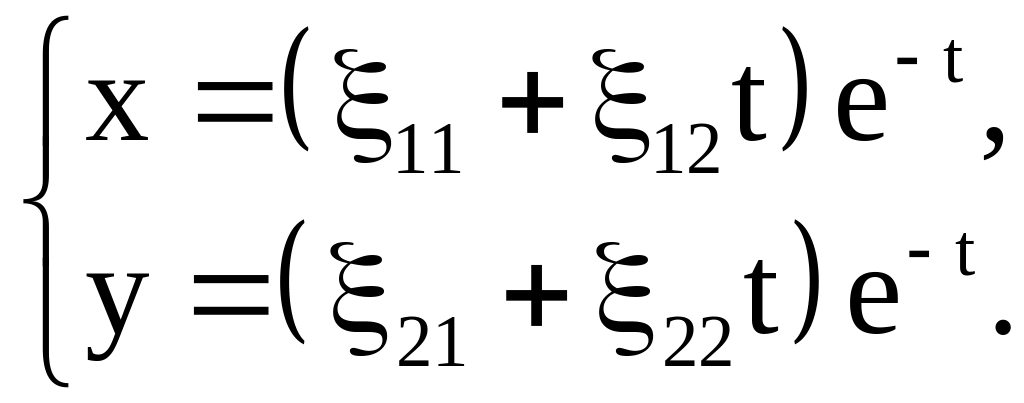 (25)
(25)
Тогда

Подставим
эти функции x(t),
y(t)
в исходную систему дифференциальных
уравнений; после сокращения на
![]() получим следующую систему уравнений:
получим следующую систему уравнений:
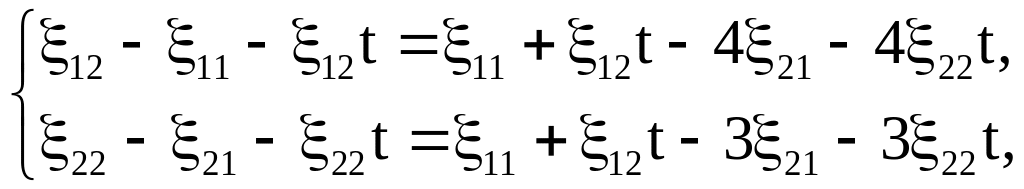
или
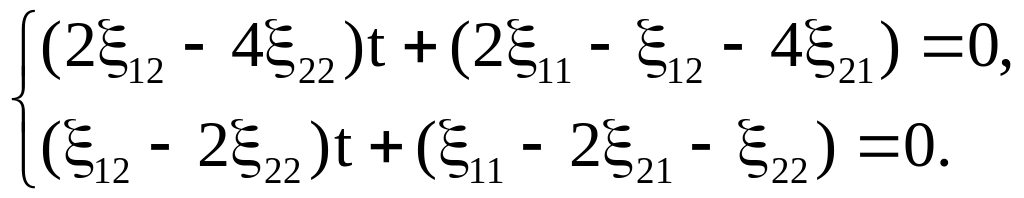
Приравняв
выражения в скобках к нулю, придем к
системе линейных однородных уравнений
с неизвестными
![]() .
.
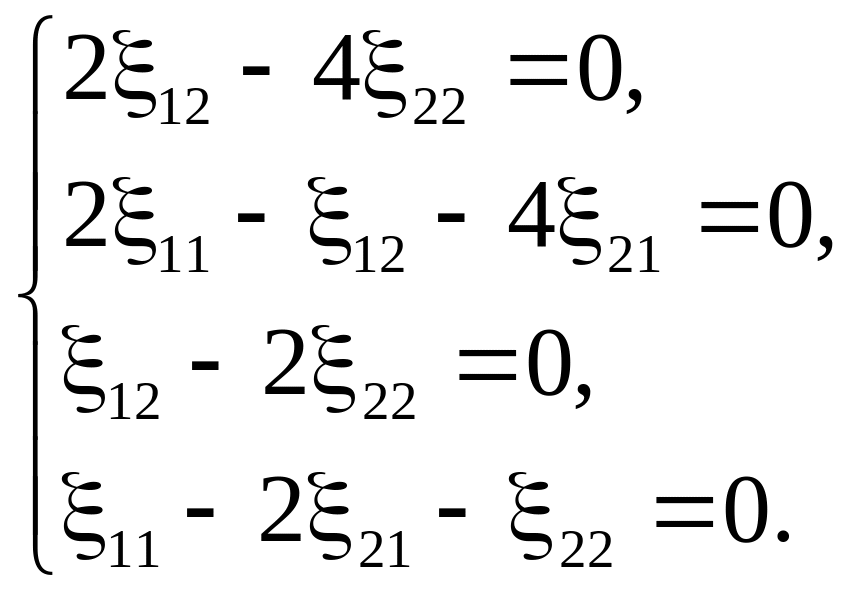 (26)
(26)
Решим
эту систему методом Гаусса, расположив
неизвестные
по порядку
![]() :
:
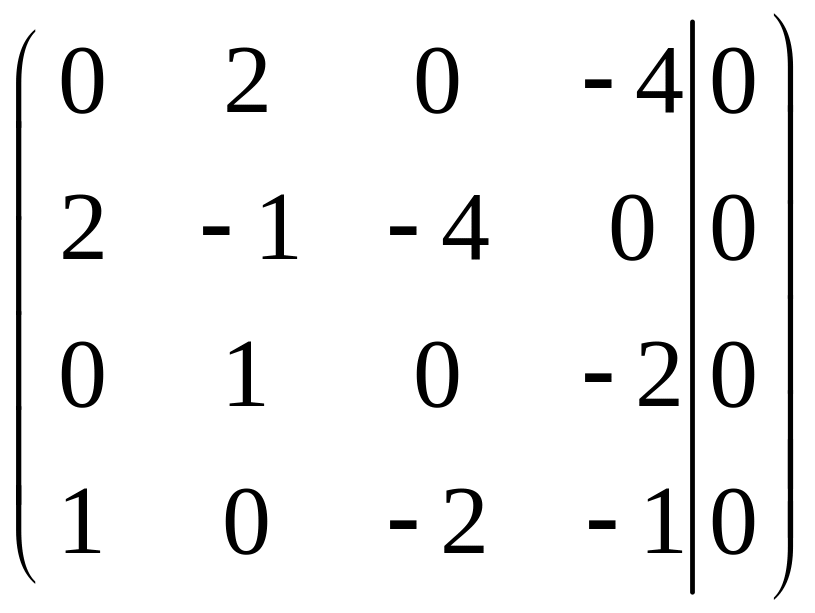
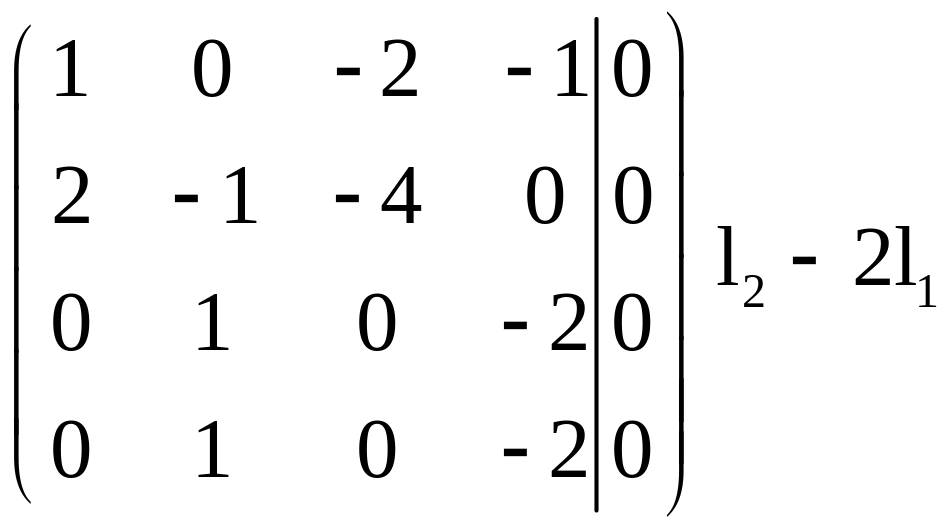
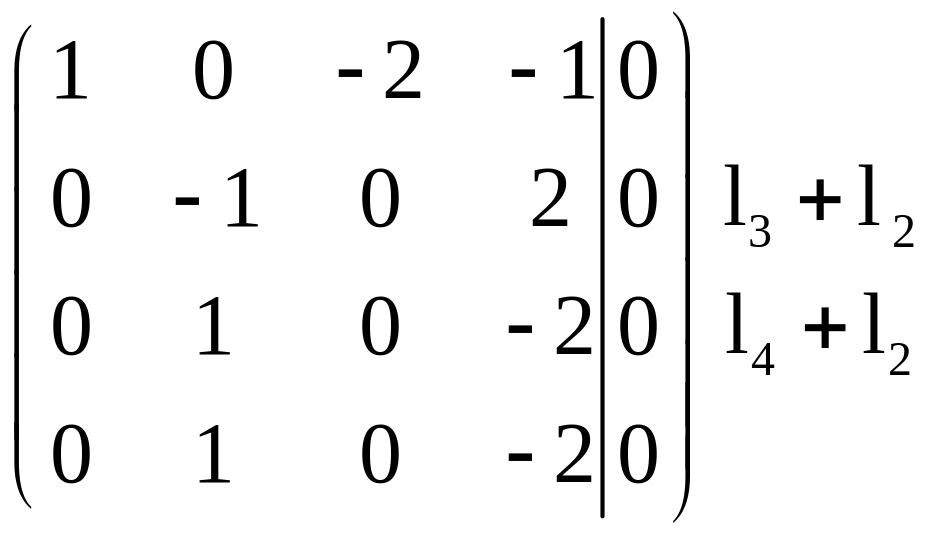
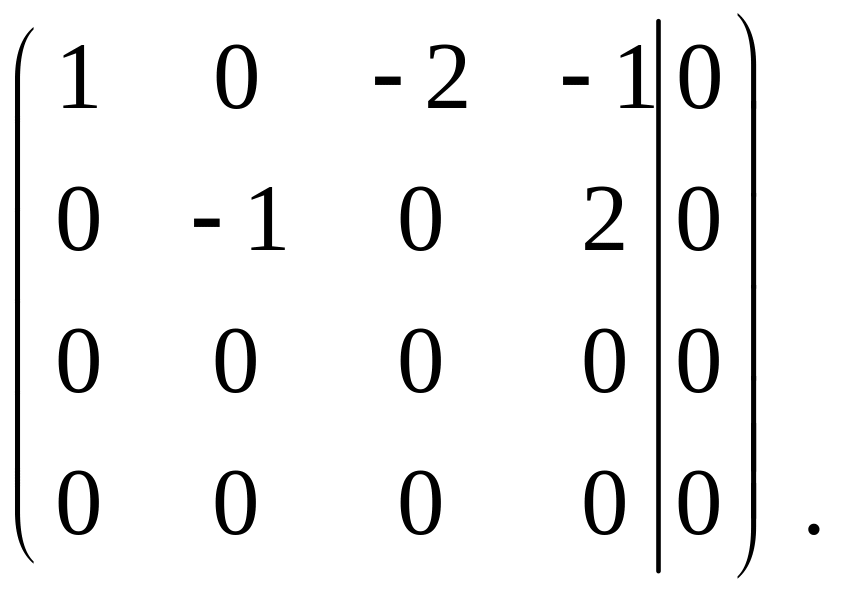
Получим, что система (26) равносильна следующей системе из двух уравнений:
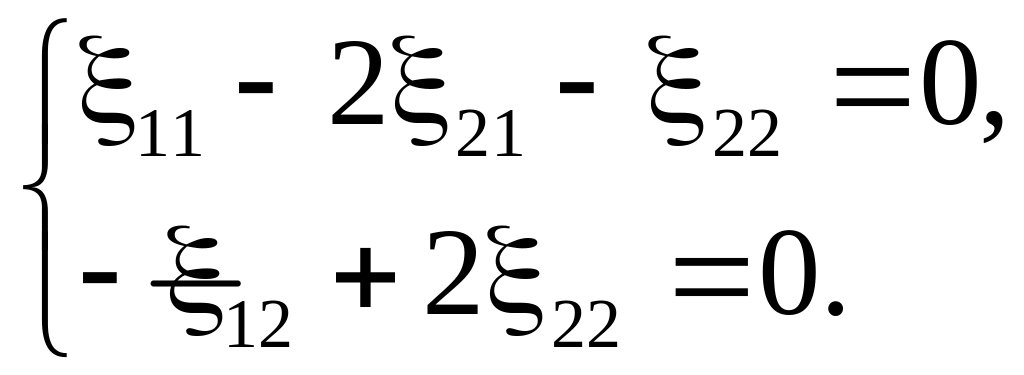
Объявим
неизвестные
![]() и
и
![]() свободными и положим
свободными и положим
![]() .
Тогда решение системы (25) запишем в виде
.
Тогда решение системы (25) запишем в виде
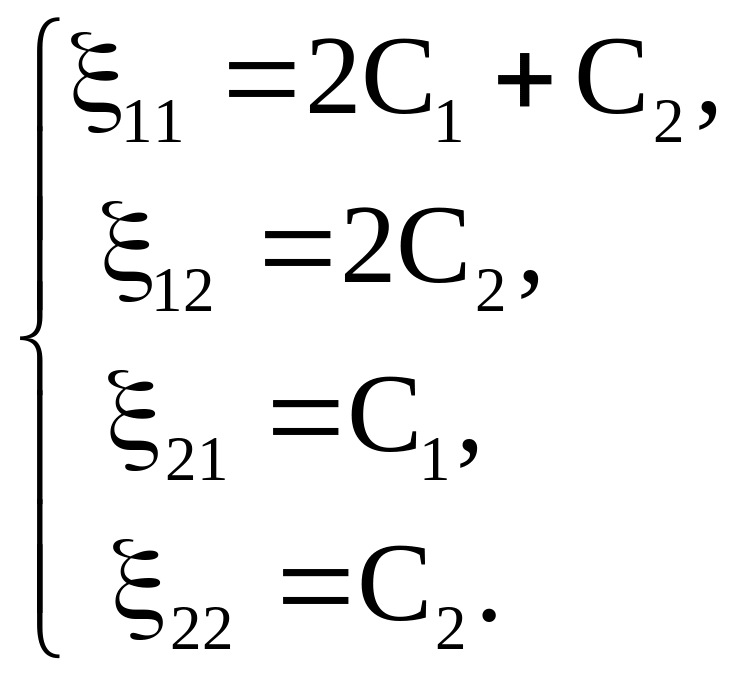
Подставим эти значения в (25), получим решение исходной системы дифференциальных уравнений в виде
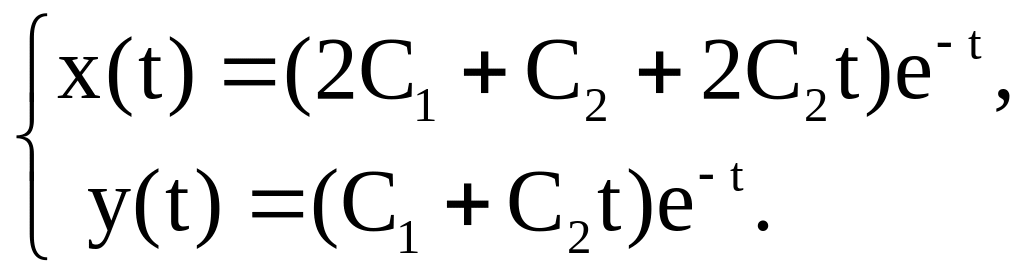
Пример 26. Решить задачу Коши для системы дифференциальных уравнений
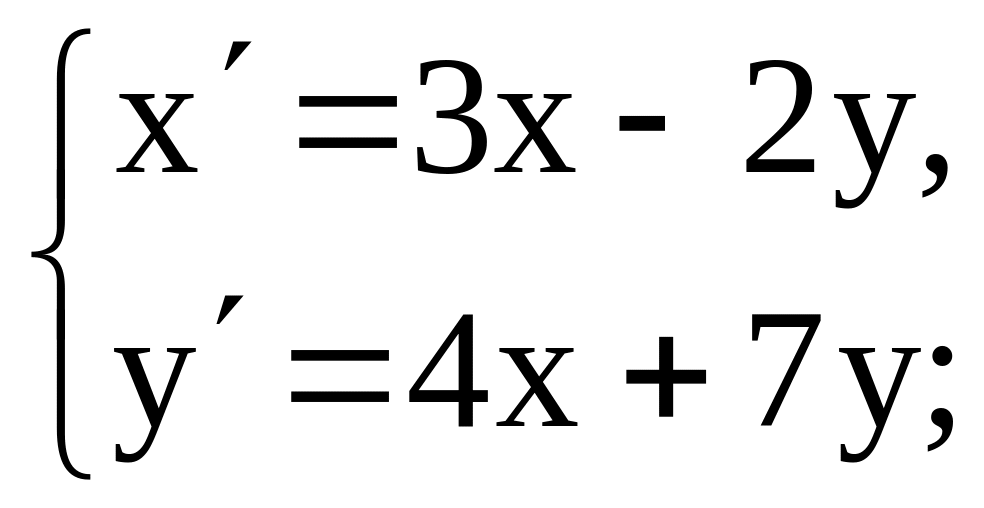 x(0)=1, y(0)=0.
x(0)=1, y(0)=0.
Решение. Сначала найдем общее решение линейной однородной системы дифференциальных уравнений. Матрицей системы является
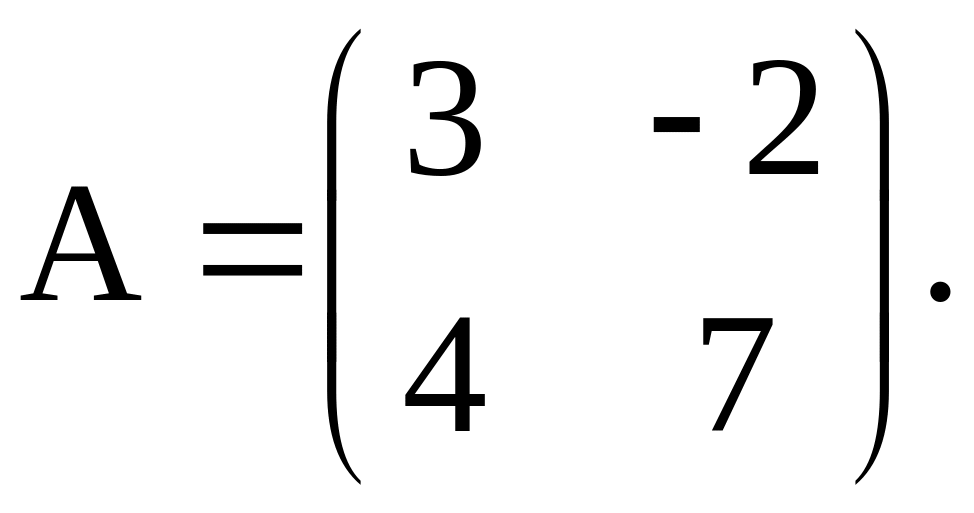
Характеристическое уравнение имеет вид
 ;
; ![]() .
.
Корнями
этого уравнения являются
![]() Найдем собственный вектор, соответствующий
собственному значению
Найдем собственный вектор, соответствующий
собственному значению
![]() :
:
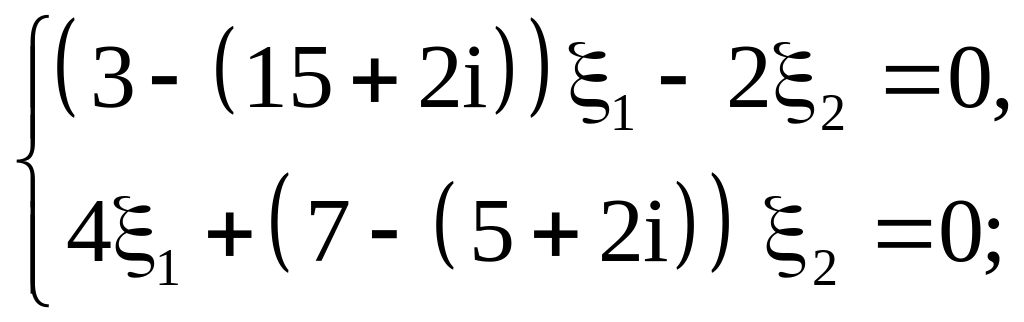
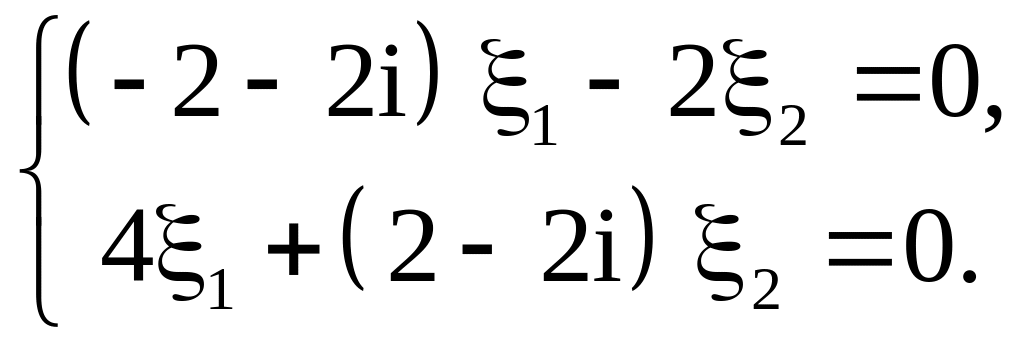
Ранг матрицы этой системы равен единице, и она равносильна уравнению
![]() .
.
Положим
![]() ,
тогда
,
тогда
![]() .
Вектор
.
Вектор
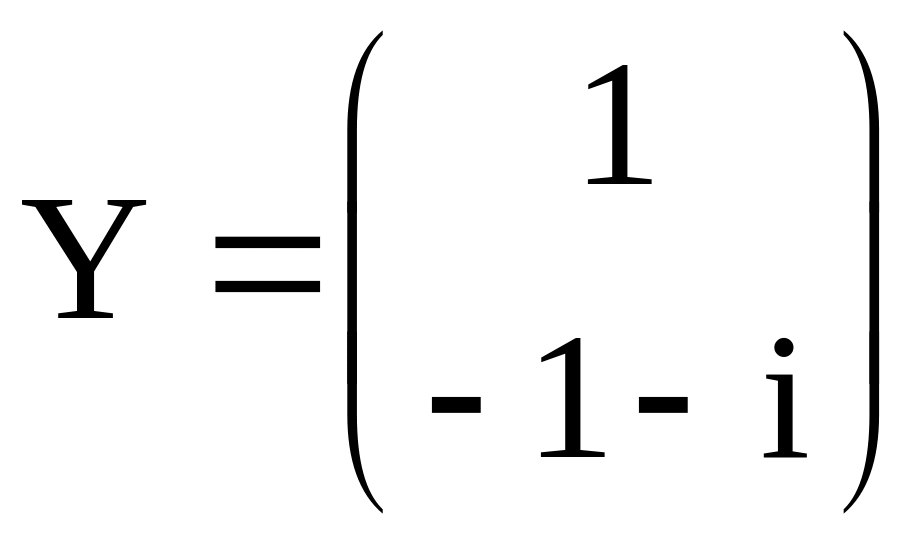 является собственным вектором матрицы
А, отвечающим собственному значению
является собственным вектором матрицы
А, отвечающим собственному значению
![]() .
Имеем
.
Имеем

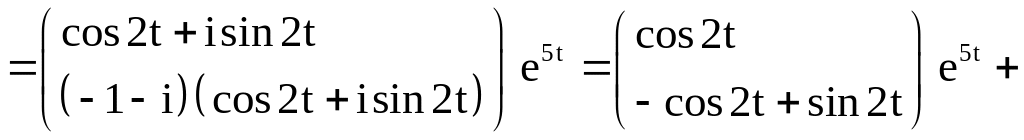

Отсюда находим пару вещественных решений системы дифференциальных уравнений, образующих ФСР:
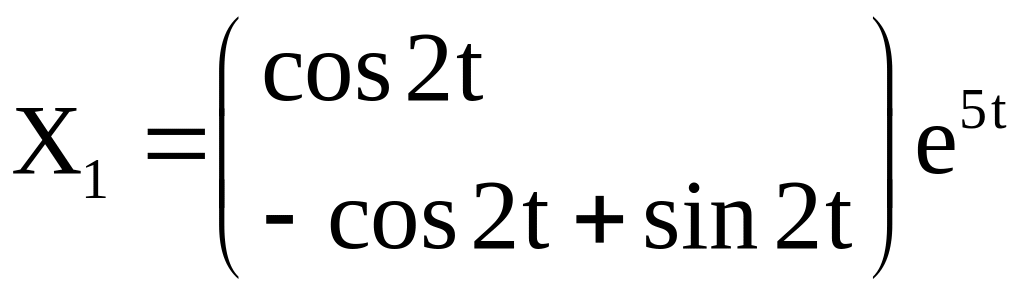 ,
,
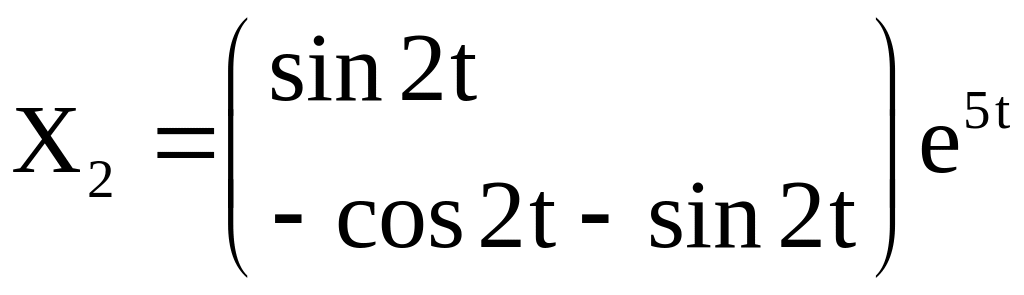 .
.
Общее решение нашей системы имеет вид
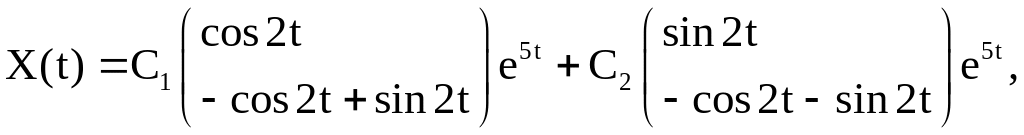
или
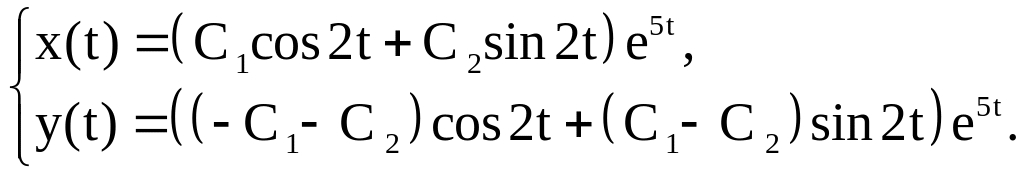
Перейдем
к решению задачи Коши. Для нахождения
коэффициентов
![]() и
воспользуемся начальными условиями:
и
воспользуемся начальными условиями:

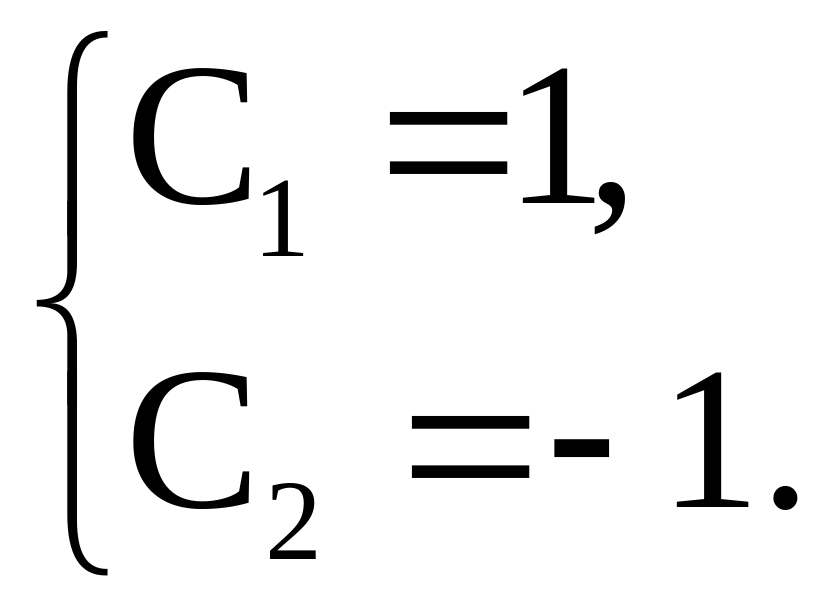
Поэтому решением нашей задачи является система