10. Метод вариации постоянных

Если известно общее решение однородного уравнения (10), то общее решение неоднородного уравнения (13) (с теми же коэффициентами ) можно найти, используя метод вариации постоянных. Пусть – ФСР однородного уравнения (10) и  – общее решение (10). Общее решение неоднородного уравнения (13) ищется в виде

, (19)

где коэффициенты рассматриваются как неизвестные функции, получающиеся путем вариации постоянных . Подстановка функции (19) в уравнение (13) приводит к следующей системе уравнений относительно :

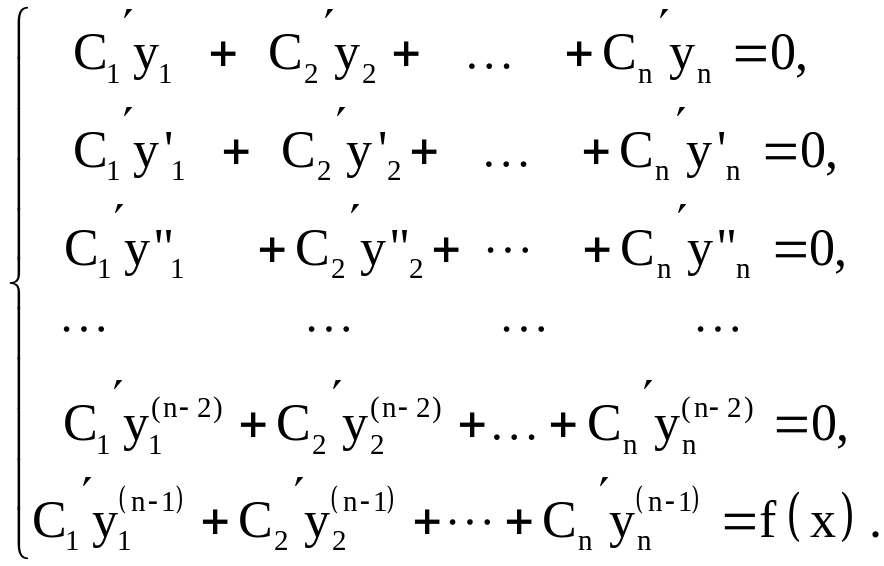
Решив эту систему и подставив найденные функции в (19), получим общее решение неоднородного уравнения (13).

Пример 21. Решить уравнение

Решение. Общим решением однородного уравнения является Будем искать общее решение неоднородного уравнения в виде

где – функции, удовлетворяющие системе

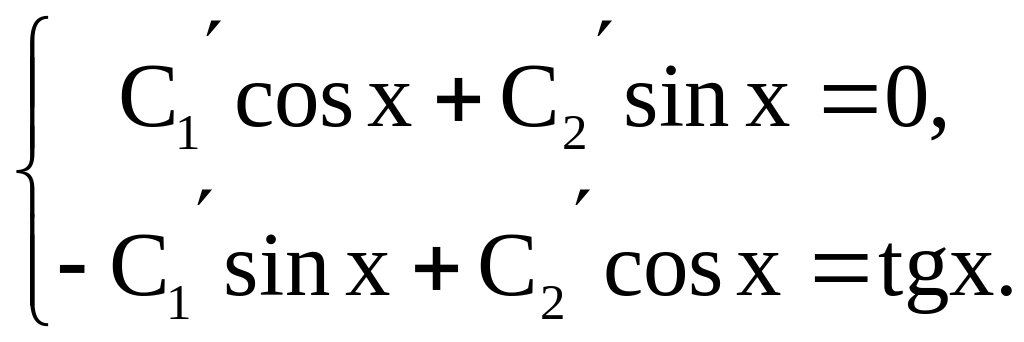
Решим эту систему методом Крамера:

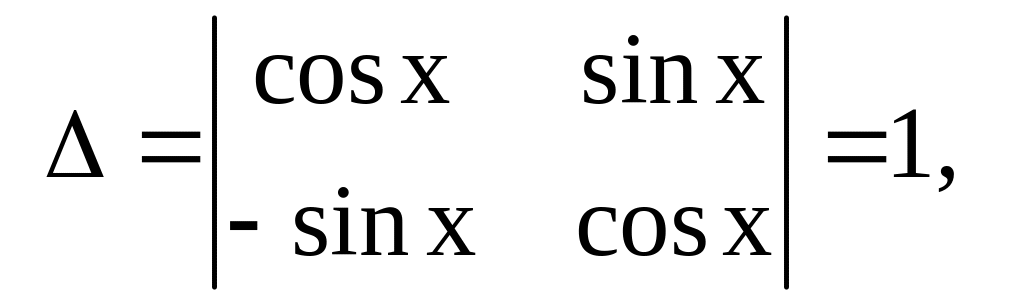
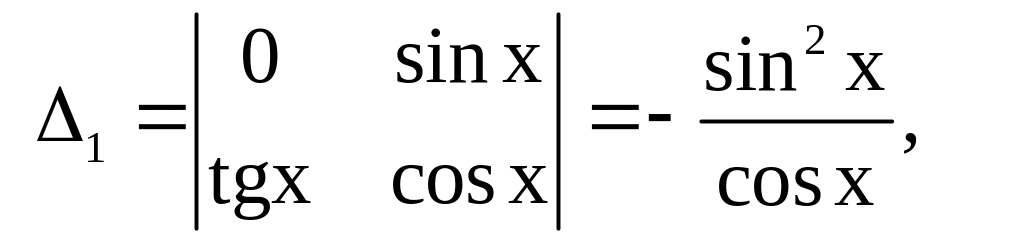
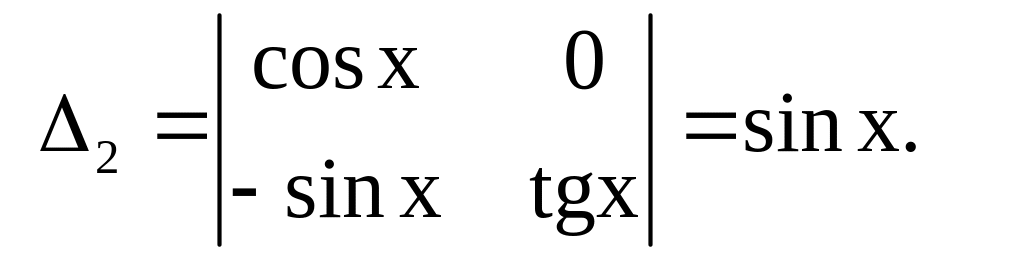
Отсюда находим

,

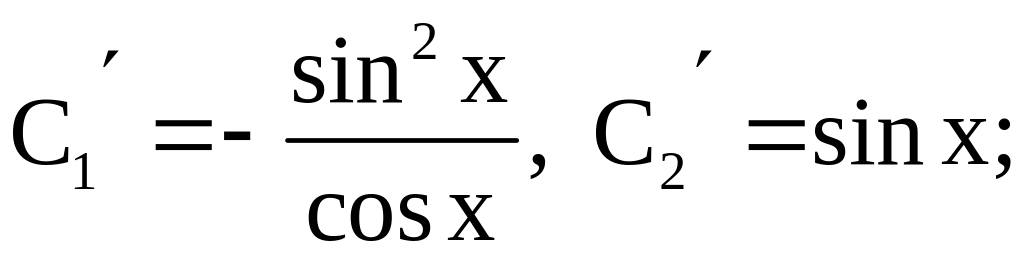
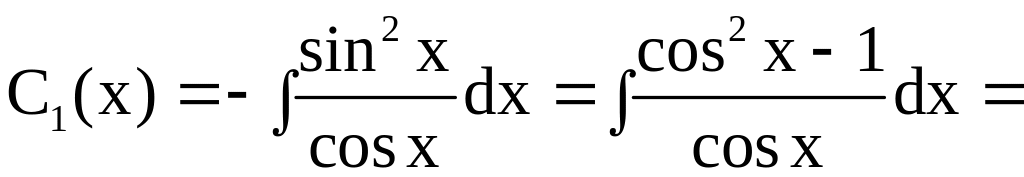
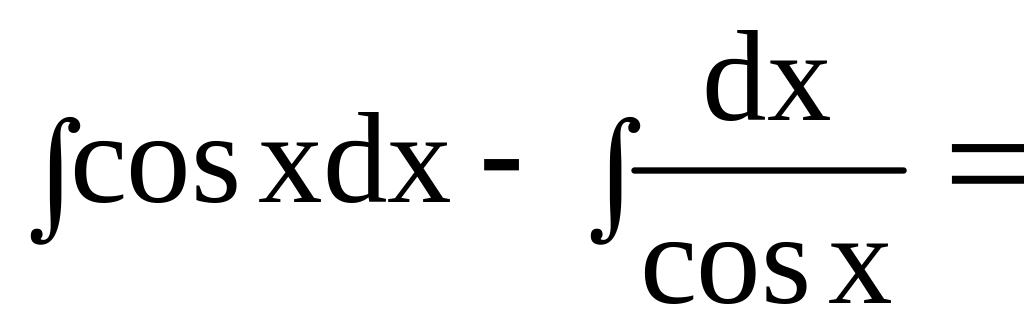
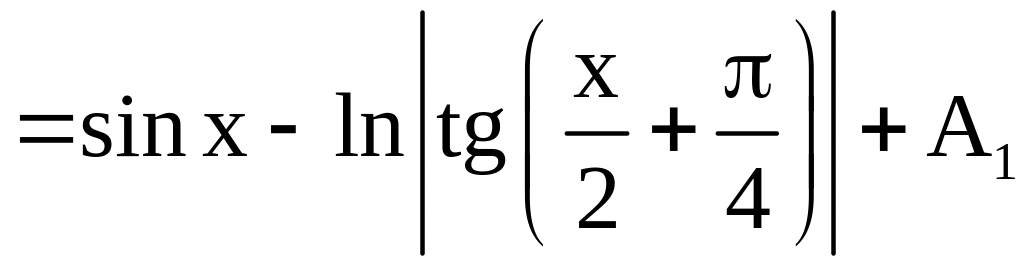Таким образом, общим решением неоднородного уравнения является

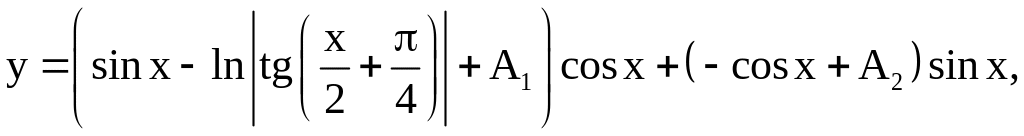
или

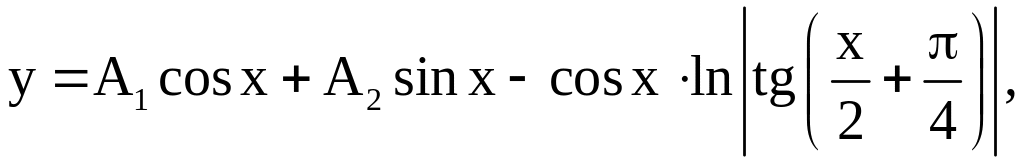
где – произвольные постоянные.

11. Задачи, приводящие к дифференциальным уравнениям

Пример 22. Найти кривую, проходящую через точку (1;2) и обладающую тем свойством, что площадь треугольника, образованного касательной, осью абсцисс и радиус-вектором, проведенным к точке касания, есть величина постоянная, равная 5.

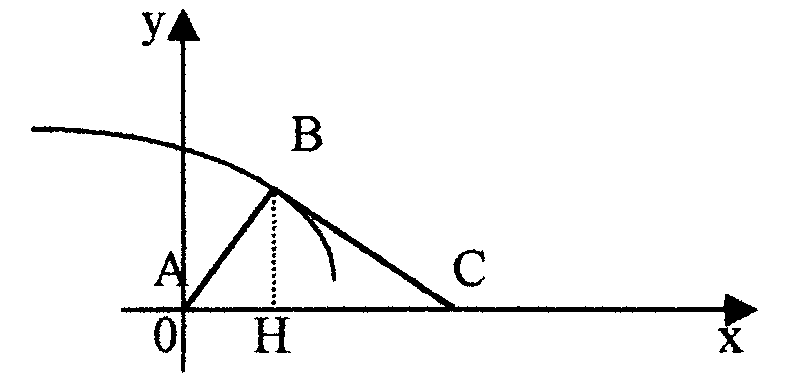
Решение. Пусть B(x;y) – точка касания, BC – отрезок касательной,

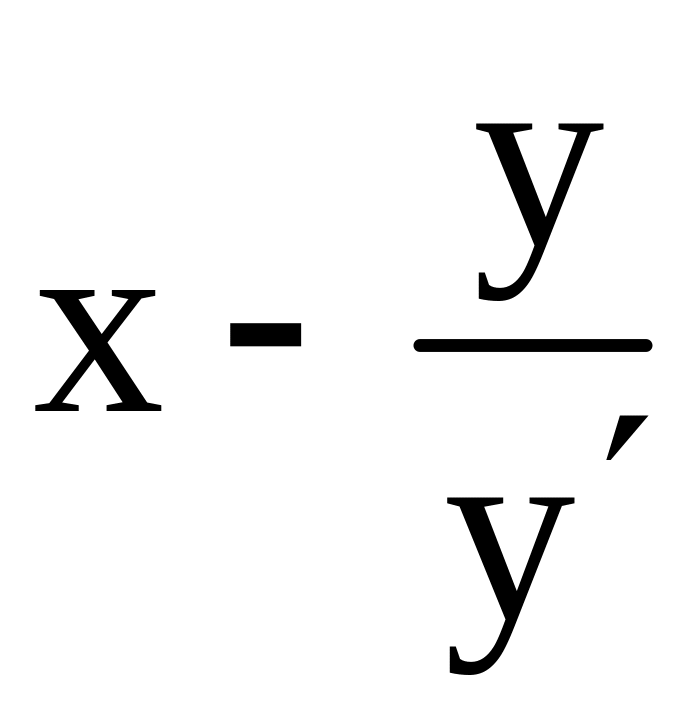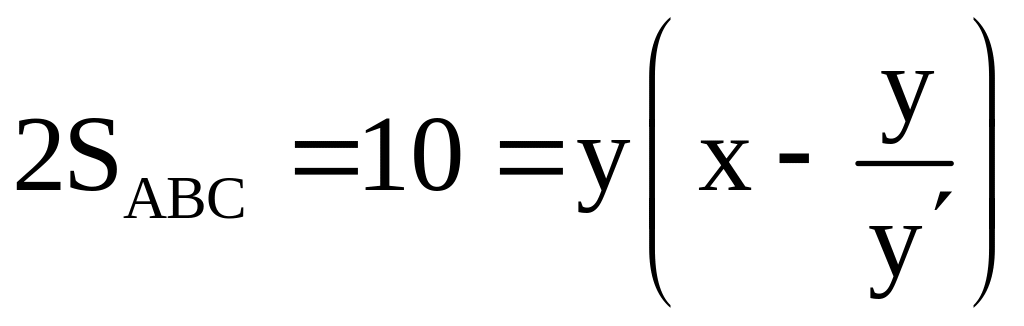AB – радиус-вектор, BH – высота треугольника ABC, площадь которого равна 5. Если , то и длина основания AC равна . Так как , то . С учетом того, что 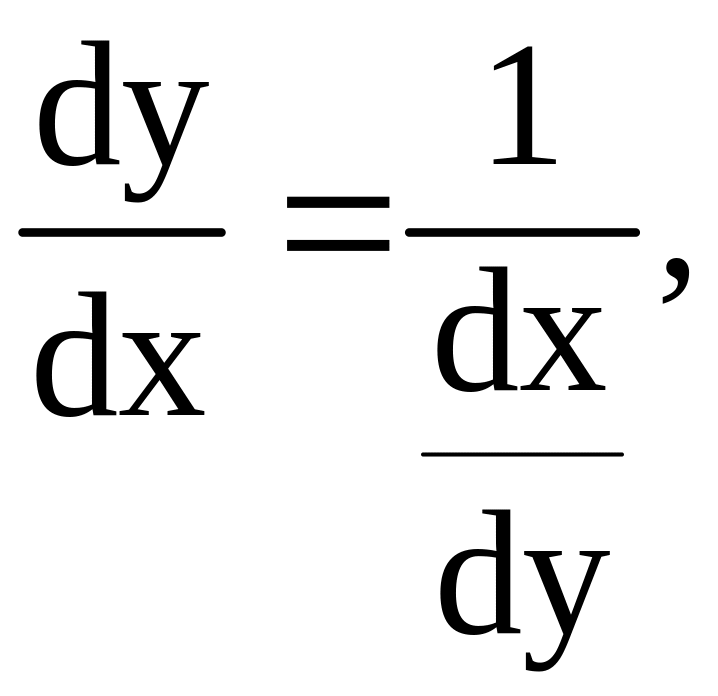это уравнение сводится к линейному относительно x(y) дифференциальному уравнению с начальным условием . Решением этого линейного дифференциального уравнения является 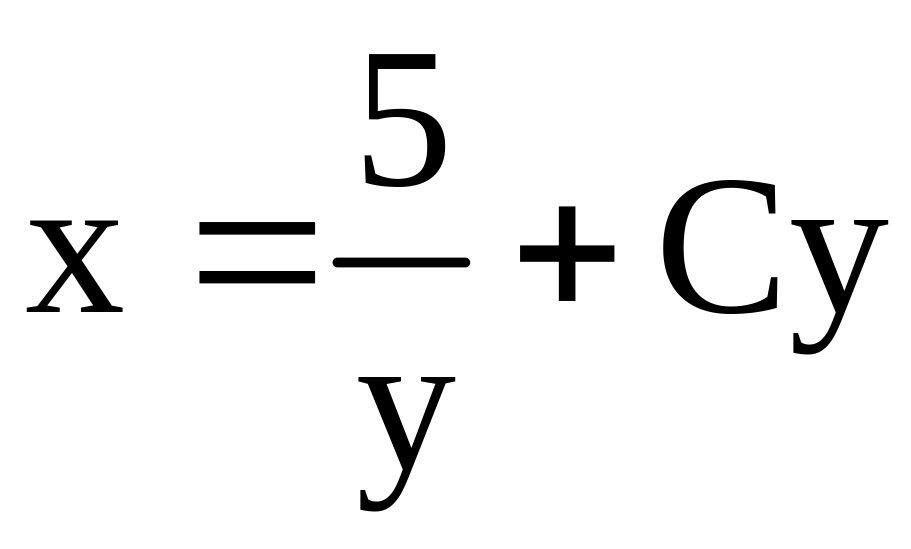. Из дополнительного условия следует, что С= –3/4. Таким образом, искомая кривая задается уравнением .

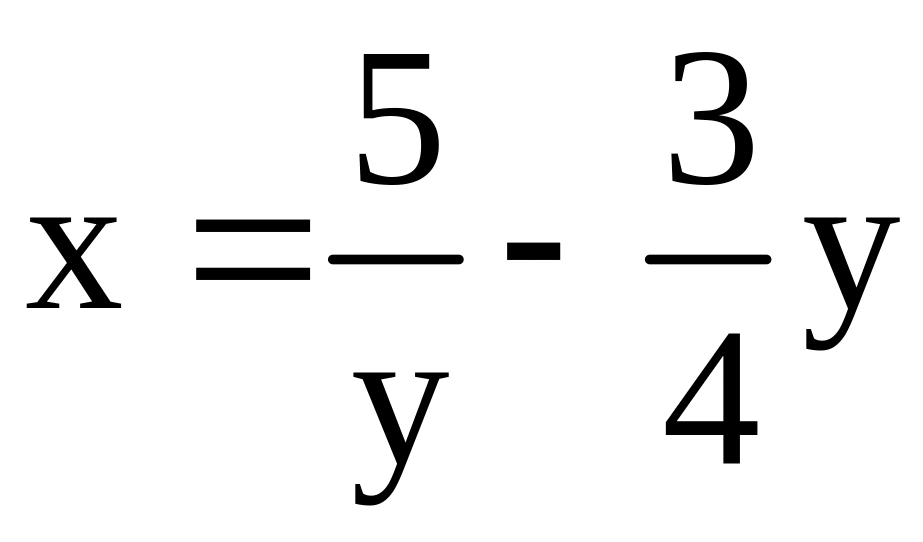Пример 23. Рыболовецкий бот движется по заливу со скоростью 25 км/ч. Через 1 минуту после остановки двигателя его скорость составила 15 км/ч. Считая, что сопротивление воды пропорционально квадрату скорости лодки, найти скорость лодки через 3 минуты после остановки двигателя.

Решение. Пусть v(t) – скорость лодки в момент времени t. Из второго закона Ньютона и условия задачи следует, что 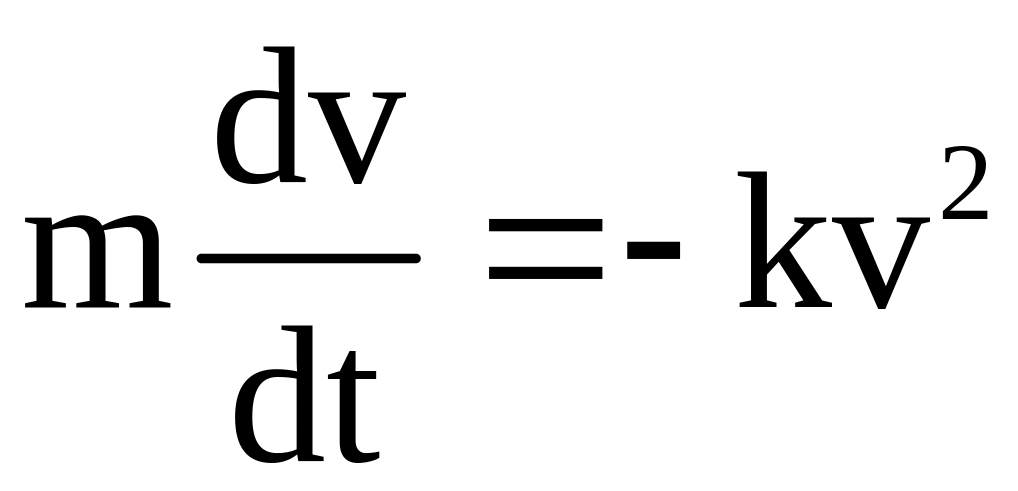. Отсюда 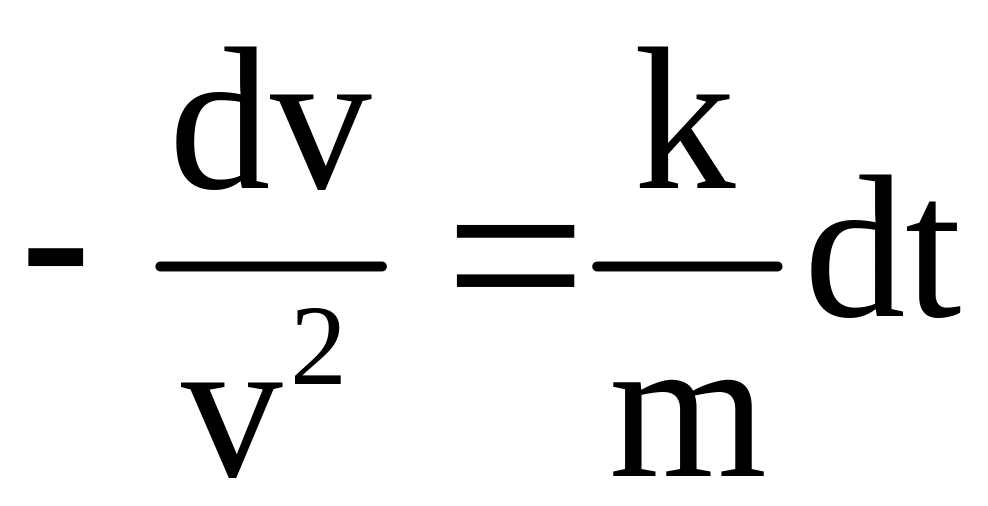и, следовательно, .

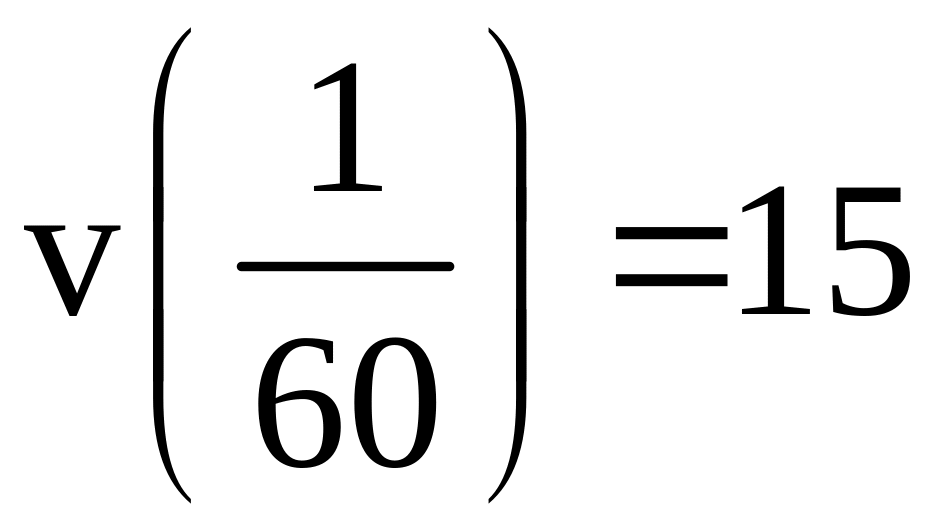Учитывая начальные условия , находим , а из условия следует, что 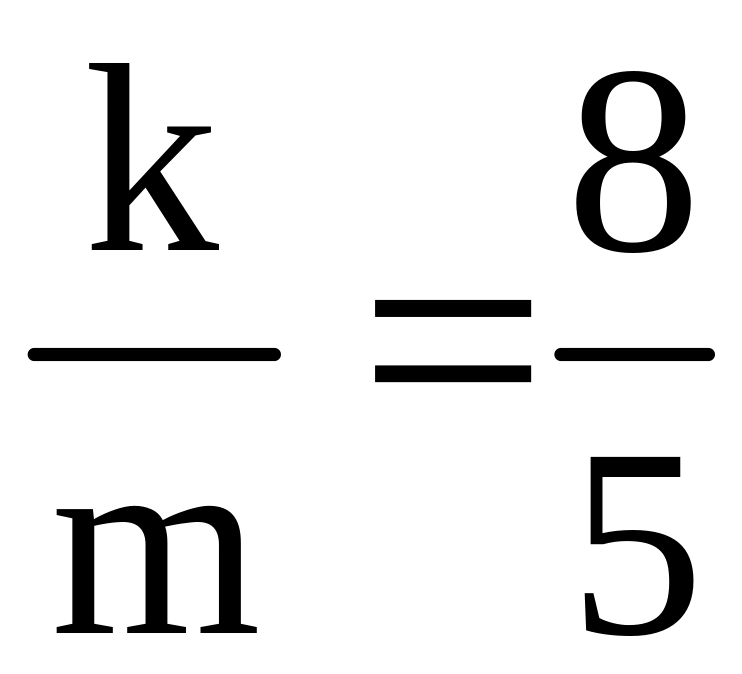. Наконец,

.

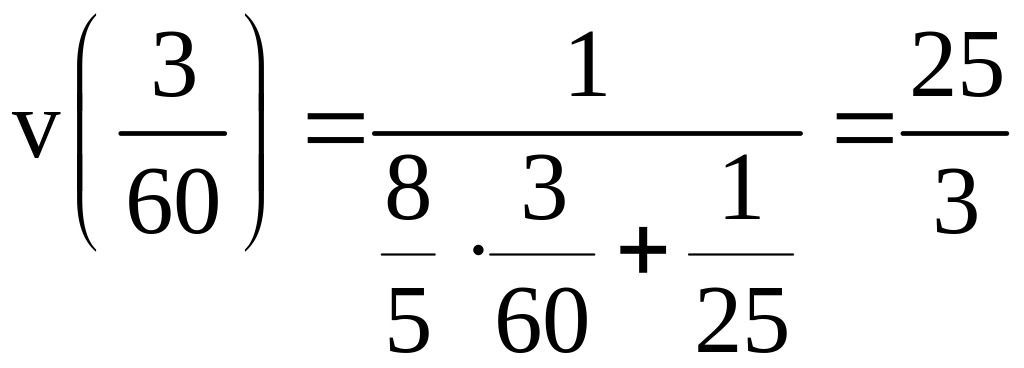12. Системы дифференциальных уравнений. Линейные системы

Система уравнений вида

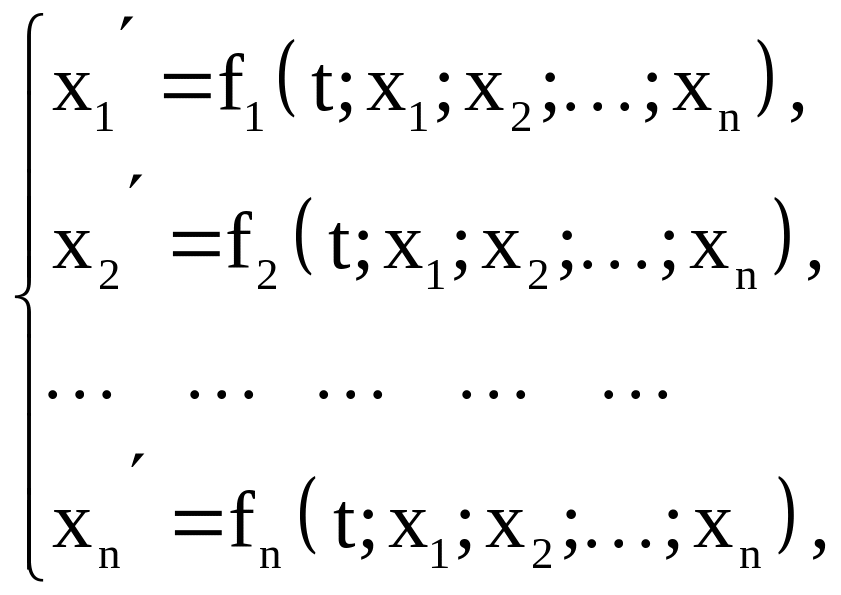(20)

где t – независимое переменное, – искомые функции, называется нормальной системой дифференциальных уравнений n-го порядка. Решением этой системы на интервале называется совокупность функций , которые при подстановке их в систему (20) обращают уравнения системы в тождества на .

Как правило, система (20) имеет бесконечное множество решений ,  , , при этом каждая искомая функция зависит от n не зависящих друг от друга параметров .

Задача Коши системы (20) ставится следующим образом: требуется найти решение системы (20), удовлетворяющее начальным условиям

(21)

При некоторых ограничениях на функции задача Коши (20) – (21) имеет единственное решение.

Нормальная линейная однородная система n-го порядка имеет вид

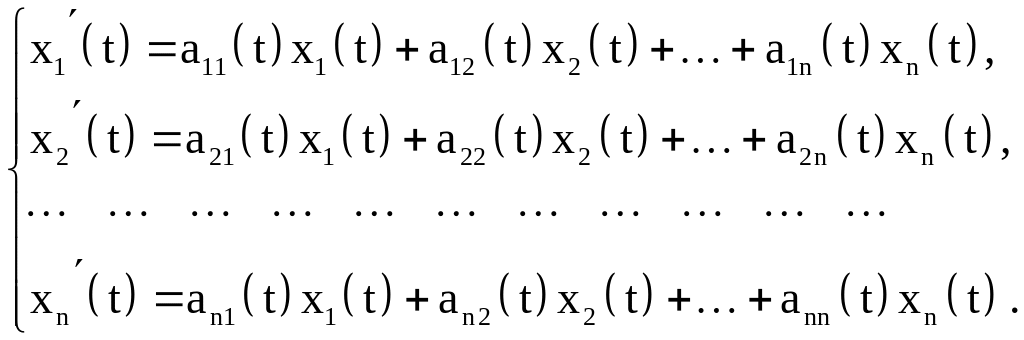(22)

Если обозначить

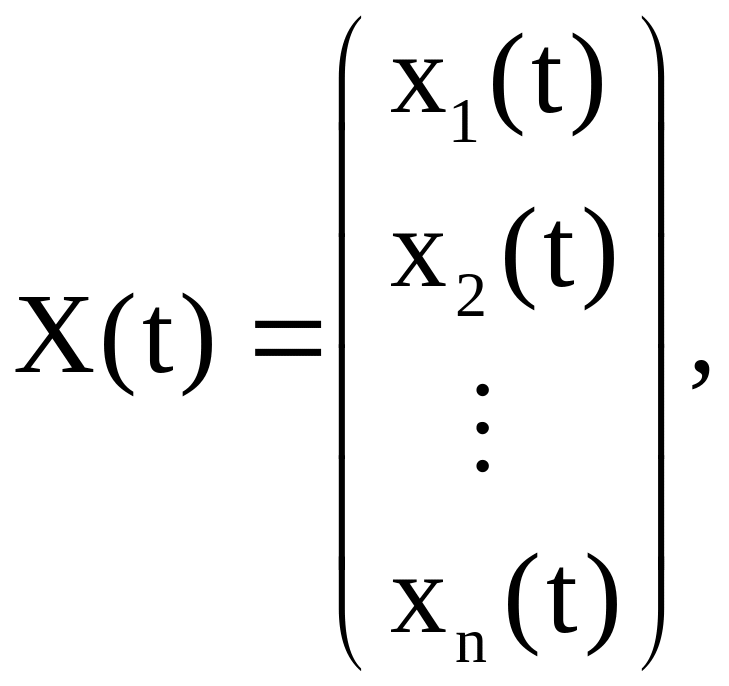
то системе (22) можно придать компактный вид, записав ее в матричной форме: .

Система из n линейно независимых решений ,

где 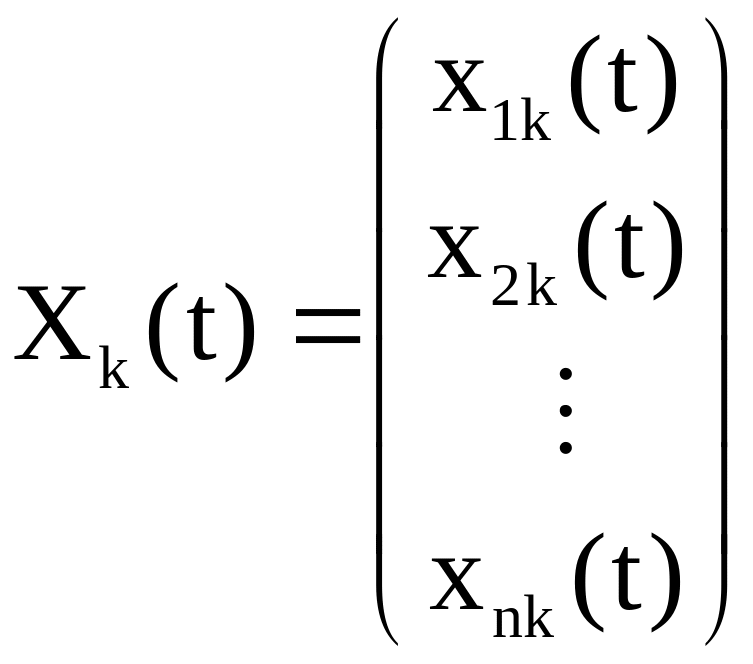, называется фундаментальной системой решений (ФСР) системы (22).

Теорема 4. Если – ФСР системы (22), то общее решение системы (22) имеет вид

,

где – произвольные постоянные.

Линейная неоднородная система n-го порядка имеет вид

(23)

или в матричной форме ,

где .

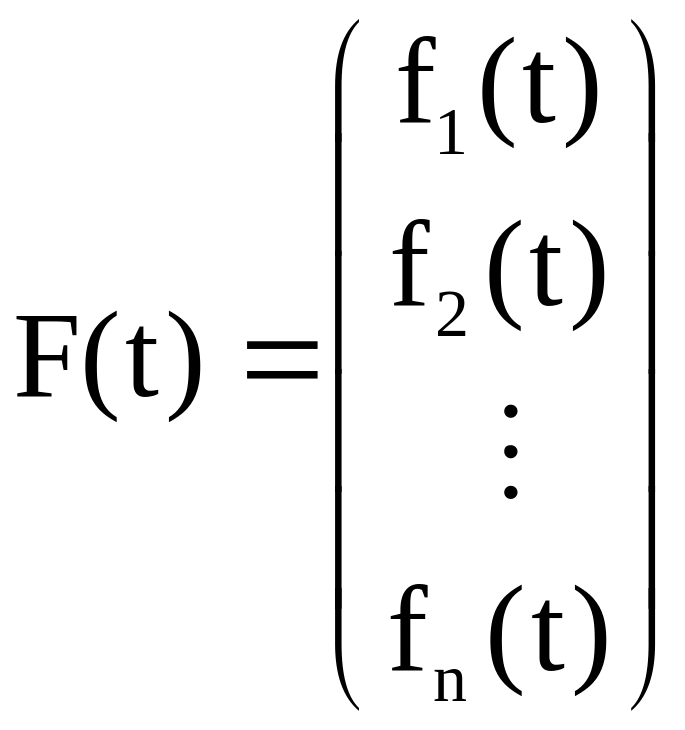Теорема 5. Пусть – некоторое частное решение системы (23), а – ФСР соответствующей однородной системы (22), т.е. имеющей те же коэффициенты . Тогда общее решение неоднородной системы (23) имеет вид

,

или, короче, ,

где  – общее решение однородной системы (22), соответствующей системе (23).

В общем случае невозможно найти ни ФСР однородной системы (22), ни частное решение неоднородной системы (23). Но задача намного упрощается, если мы имеем дело с системами с постоянными коэффициентами.