Порядок
такого уравнения можно понизить на k
единиц путем замены
,
при этом исходное уравнение сведется
к уравнению
Пусть
– общее
решение последнего уравнения. Тогда
общее решение исходного уравнения
находится путем k-кратного интегрирования
функции
Пример 10. Решить задачу Коши
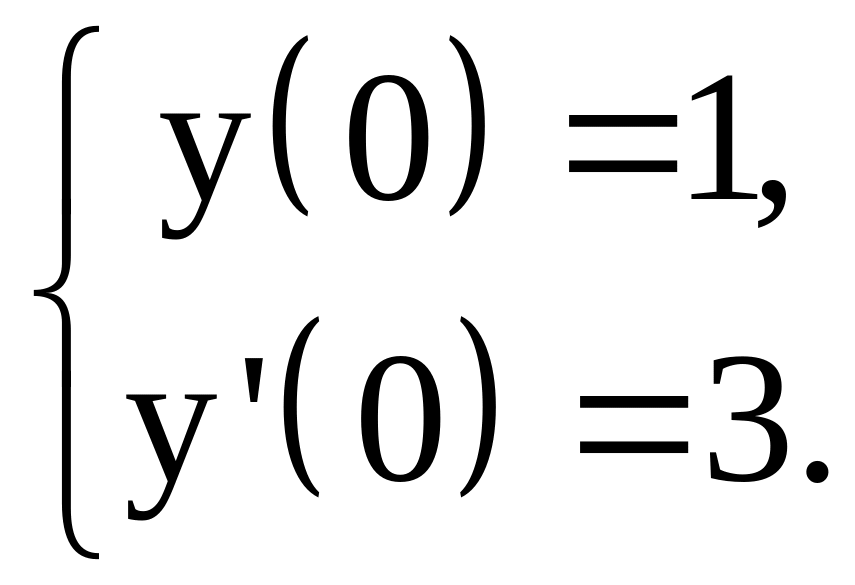
Решение.
Сначала найдем общее решение
дифференциального уравнения
В это уравнение не входит явно неизвестная
функция
.
Сделаем замену
Уравнение примет вид
Это уравнение с разделяющимися переменными
.
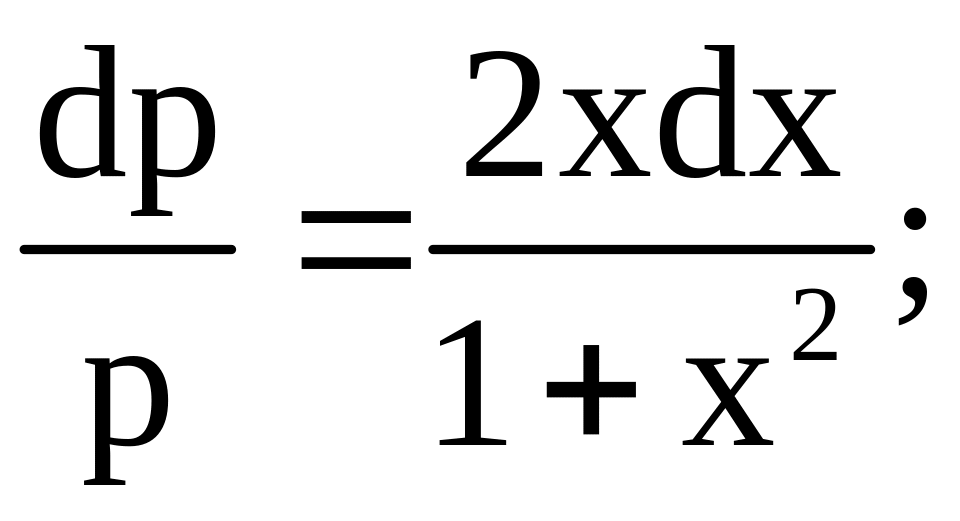
Следовательно,
Для
нахождения
и
воспользуемся начальными условиями:
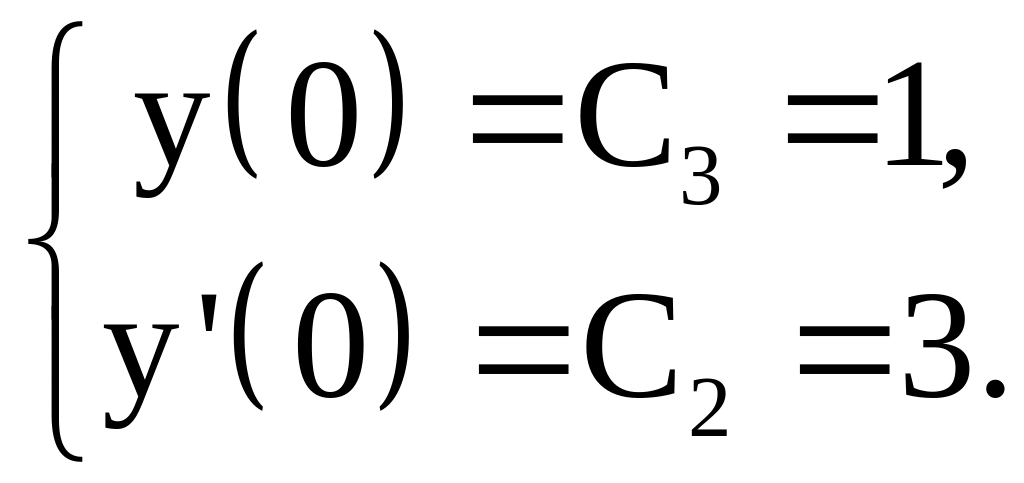
Таким образом, решением нашей задачи является
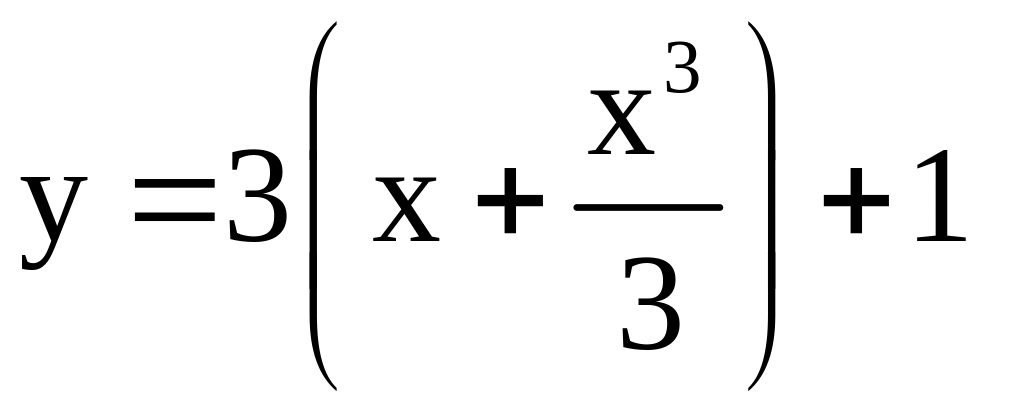или
Б. Дифференциальное
уравнение, не содержащее явно независимое
переменное:
Порядок
такого уравнения можно понизить на
единицу путем подстановки
.
При этом уравнение примет вид
.
Пример
11. Решить
уравнение
Решение.
Введем новое
переменное
Тогда
Наше уравнение примет вид
1)
2)
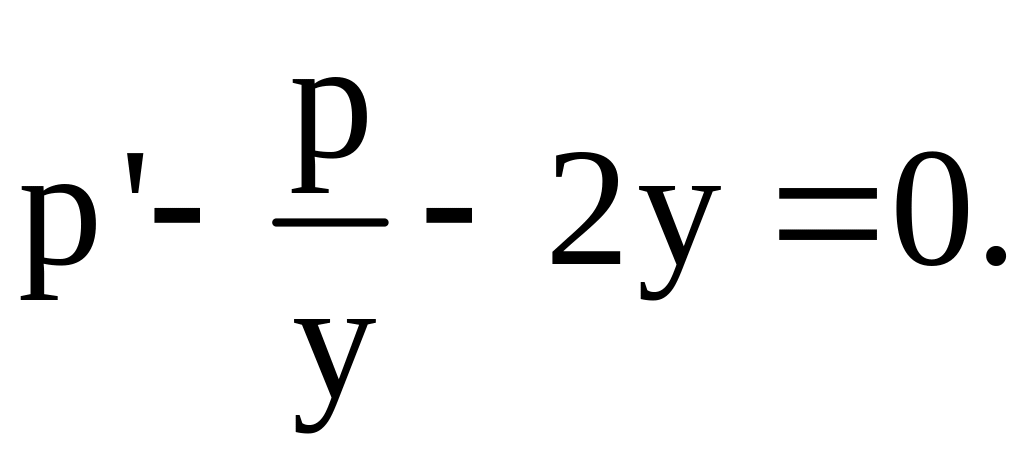Это линейное уравнение. Сделаем
подстановку
,
тогда
Имеем
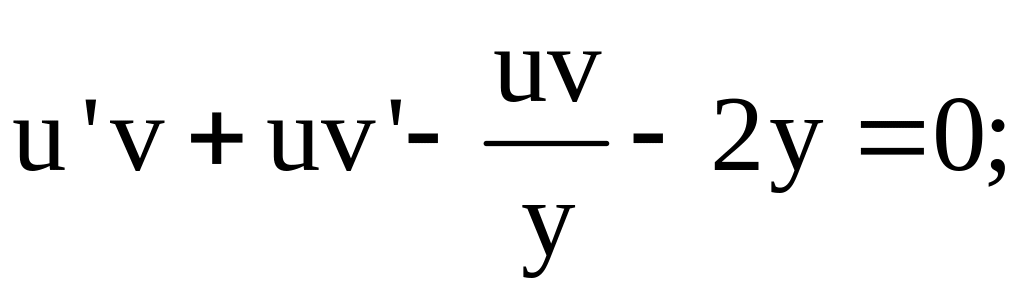
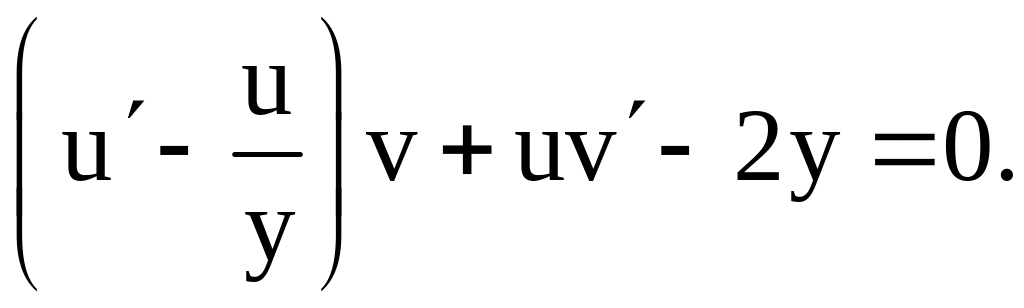
Решим систему
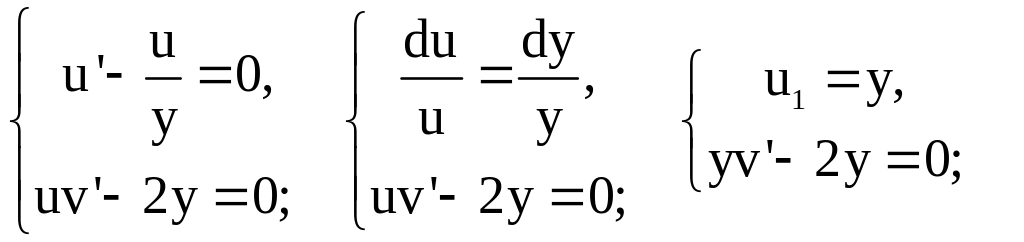
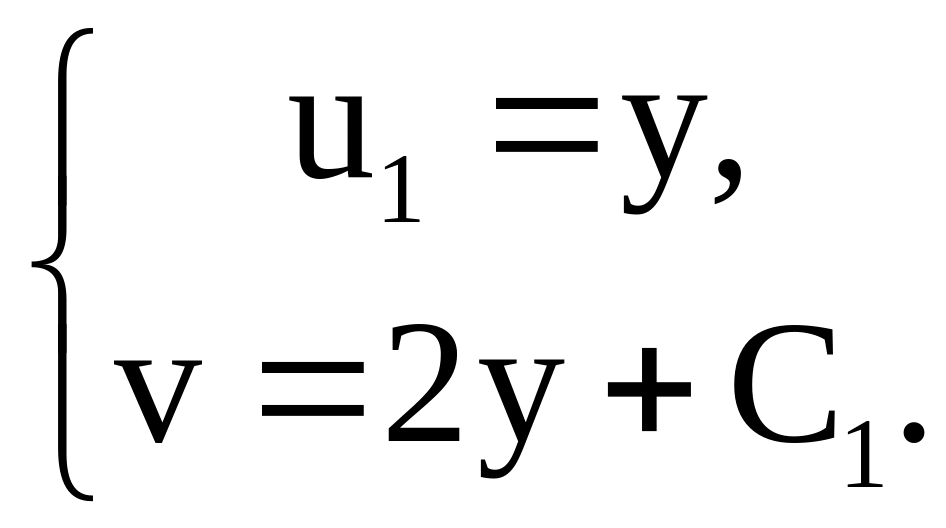
Вспомним,
что
;
;
.
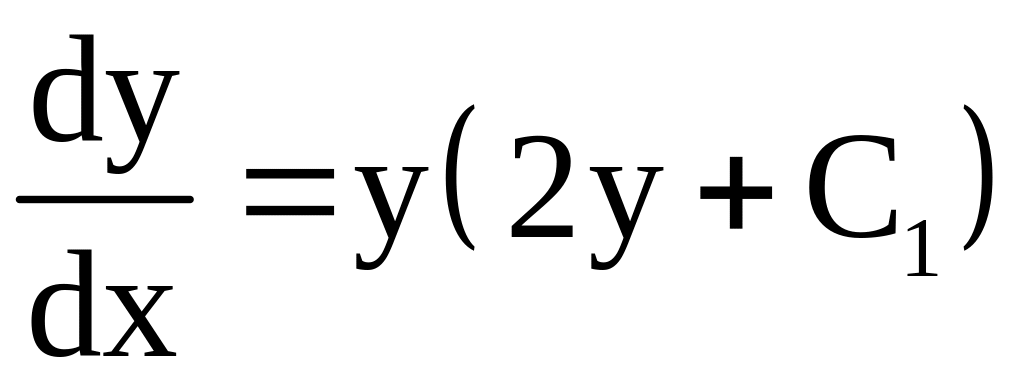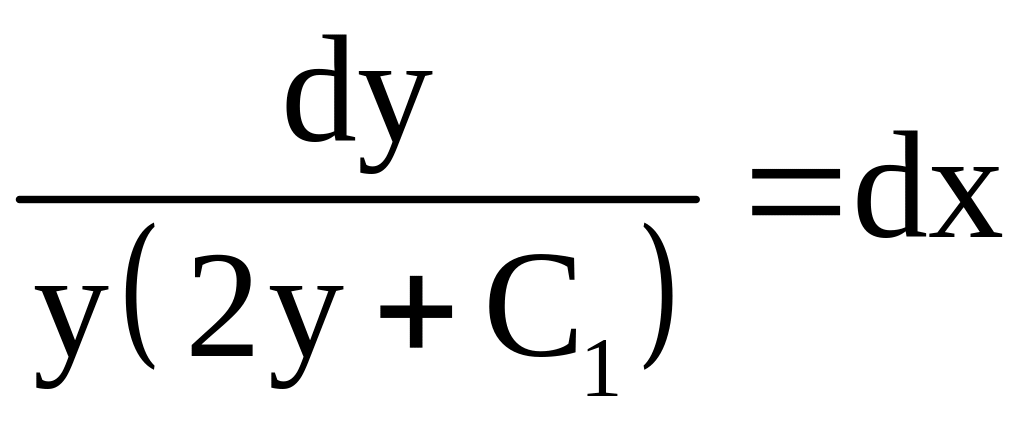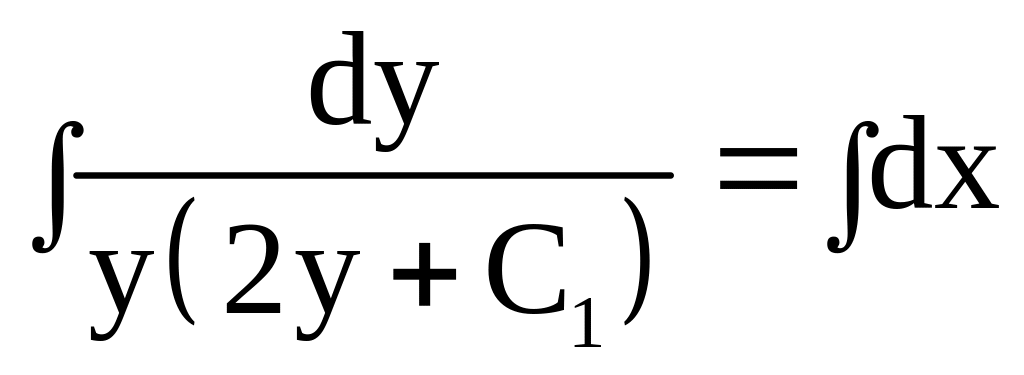Представим
функцию
в виде суммы простых дробей:
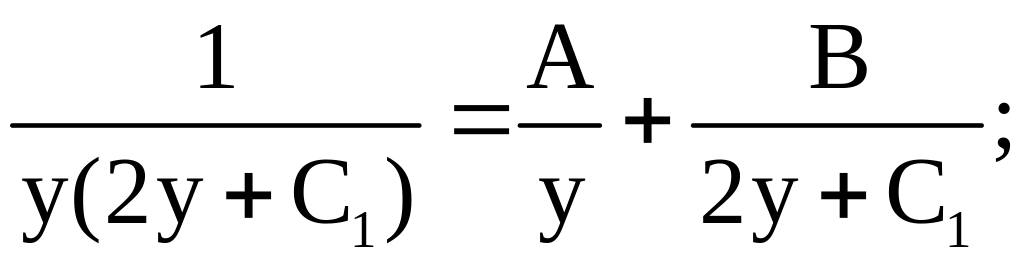
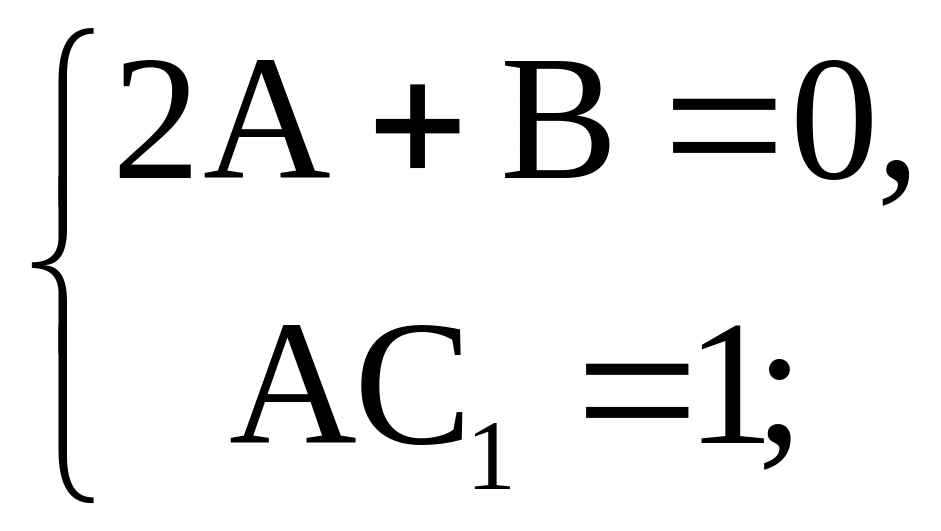
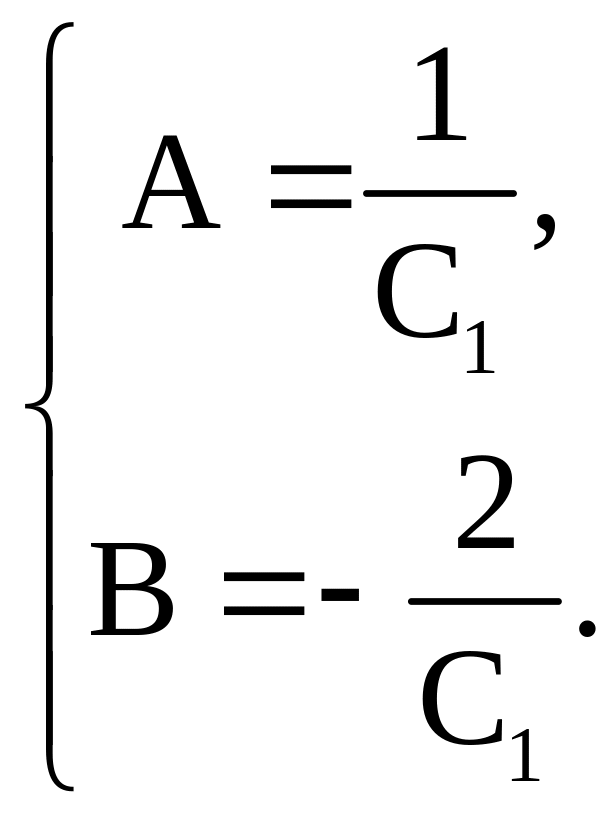
Отсюда находим
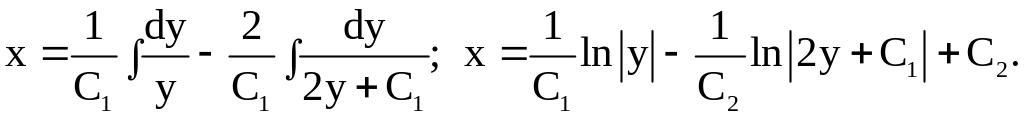
Это и есть общее решение исходного уравнения.
8. Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами
Линейным однородным дифференциальным уравнением (ЛОДУ) n-го порядка называется дифференциальное уравнение вида
(10)
где
известные функции,
искомая
функция.
Система
функций
называется линейно-зависимой, если
существуют числа
не все равные нулю и такие что
Если же последнее равенство возможно
лишь при
то система функций
называется линейно независимой.
Теорема 1.
Пусть
линейно
независимая система решений уравнения
(10). Тогда общее решение уравнения (10)
имеет вид
где
произвольный
набор чисел.
Система
линейно независимых решений
уравнения (10) называется фундаментальной
системой решений (ФСР) уравнения (10).
В
общем случае найти фундаментальную
систему решений уравнения (10), а значит
и его общее решение, очень сложно; в
большинстве случаев эта задача
неразрешима. Однако задача заметно
облегчается, если
являются постоянными величинами.
Для решения ЛОДУ с действительными постоянными коэффициентами
(11)
составляется характеристическое уравнение
(12)
Зная корни уравнения (12) , можно составить ФСР уравнения (11).
А. Каждому
действительному простому корню
ставится в соответствие функция
–
частное решение уравнения (11).
Б. Каждому действительному корню кратности k ставится в соответствие следующий набор из k частных решений (11):
В. Каждой
паре комплексно-сопряженных простых
корней
уравнения (12) ставится в соответствие
следующая пара частных решений уравнения
(11):
Г. Каждой
паре комплексно-сопряженных корней
кратности k ставится в соответствие
следующий набор из 2-х частных решений
уравнений (11):
;
.
Следуя указанному правилу, строится ФСР уравнения (11) и находится общее решение этого уравнения как линейная комбинация элементов фундаментальной системы решений.
Пример
12. Решить
уравнение
.
Решение.
Составим и решим характеристическое
уравнение
простые
корни. Значит, функции
образуют
ФСР дифференциального уравнения.
Следовательно, общее решение уравнения
имеет вид
где
произвольные
числа.
Пример
13. Решить
уравнение
Решение.
Характеристическое
уравнение
имеет один двукратный корень
Ему соответствует пара функций
образующая ФСР дифференциального
уравнения. Общим решением ЛОДУ является
Пример
14. Решить
уравнение
Решение.
Характеристическое уравнение
имеет пару простых попарно-сопряженных
корней
,
.
Им
соответствует пара функций
образующих ФСР дифференциального
уравнения. Общим решением уравнения
является
.
Пример
15. Решить
уравнение
Решение. Решим характеристическое уравнение
Корнями
уравнения являются: 
– корень
кратностью
2;
,
– простые корни;
,
– простые
корни. Им соответствует следующий набор
функций:
Эти функции образуют ФСР ЛОДУ. Общим решением уравнения является
9. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Линейным неоднородным дифференциальным уравнением (ЛНДУ) n-го порядка называется уравнение вида
(13)
где
–
известные функции, y(x)
– искомая функция.
Теорема 2.
Пусть
–
ФСР однородного уравнения (10) и пусть
–
некоторое частное решение уравнения
(13). Тогда общее решение уравнения (13)
имеет вид
где
–
произвольные постоянные; другими
словами, общим решением уравнения (13)
является
где
–
общее решение соответствующего
однородного уравнения, а
–
некоторое частное решение уравнения
(13).
Если
в уравнении (13)
являются постоянными величинами, а
имеет специальный вид
(14)
или
, (15)
то удается найти частное решение уравнения (13).
А.
Пусть
имеет вид (14) и число
не является корнем характеристического
уравнения соответствующего однородного
уравнения. Тогда частное решение
уравнения (13) ищется в виде
где
коэффициенты
находятся путем подстановки
в уравнение (13).
Б. Пусть имеет вид (14) и число является корнем кратностью r характеристического уравнения соответствующего однородного уравнения. В этом случае частное решение ищется в виде
В.
Пусть
имеет вид (15) и число
не является корнем характеристического
уравнения. Тогда частное решение
ищется в виде
где
.
Г. Пусть имеет вид (15) и число является корнем кратности r характеристического уравнения. Тогда частное решение
где, как и прежде, .
Пример
16. Решить
уравнение
Решение. Общее решение этого уравнения имеет вид где – общее решение соответствующего однородного уравнения
(16)
а
–
некоторое частное решение нашего
неоднородного уравнения. Характеристическое
уравнение однородного уравнения (16)
имеет вид
отсюда находим
Таким
образом,
Найдем
Число
является простым корнем характеристического
уравнения, следовательно,
имеет вид
или
Для определения коэффициентов А и В подставим в исходное неоднородное уравнение. Имеем
Подставим в первоначальное уравнение:
Последнее равенство приводит к системе
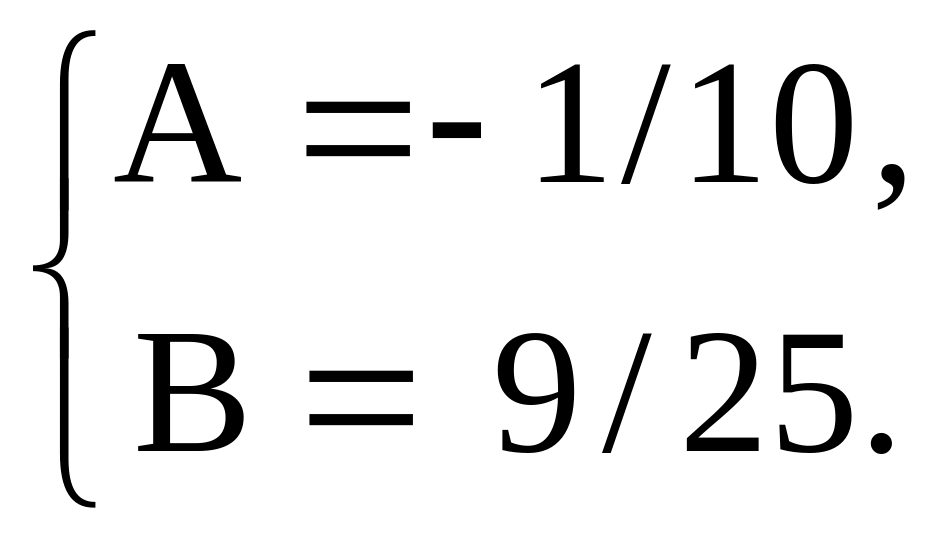
Таким образом,
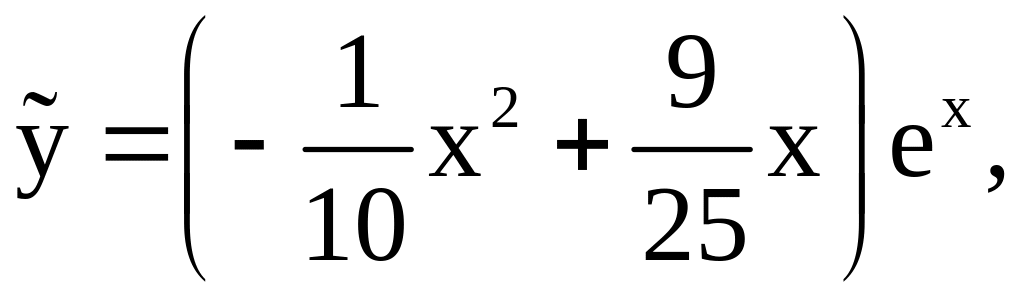
и
общим решением нашего неоднородного
уравнения является
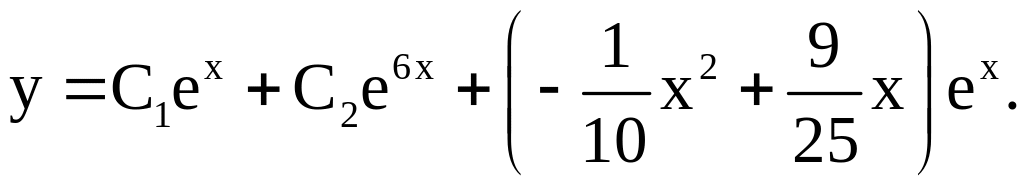
Пример
17. Решить
уравнение
Решение.
Характеристическое
уравнение
имеет простые корни
.
Общим решением соответствующего
однородного уравнения является
Правая
часть неоднородного уравнения имеет
специальный вид (15). Число
является простым корнем характеристического
уравнения, поэтому частное решение
нашего уравнения ищем в виде
Имеем
Подставим в исходное уравнение:
Приравняв
соответствующие коэффициенты, получим
систему
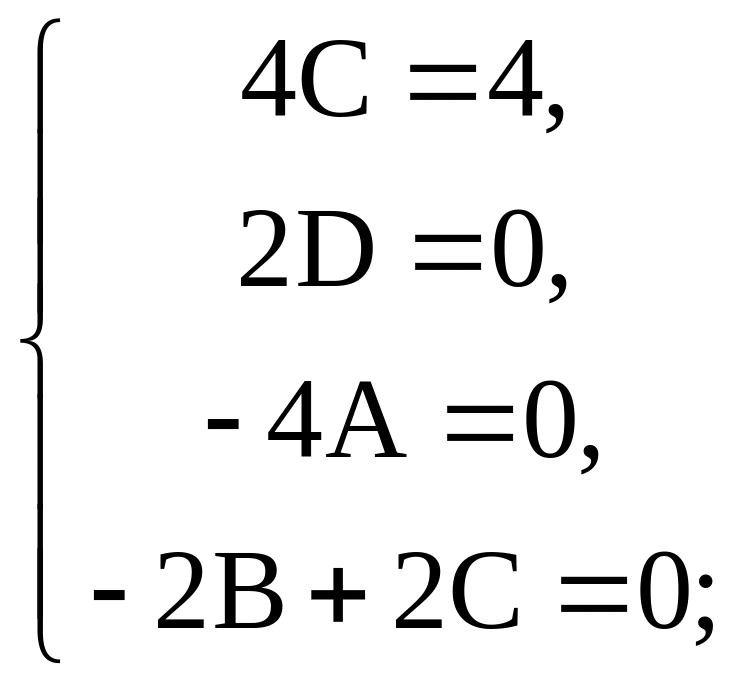
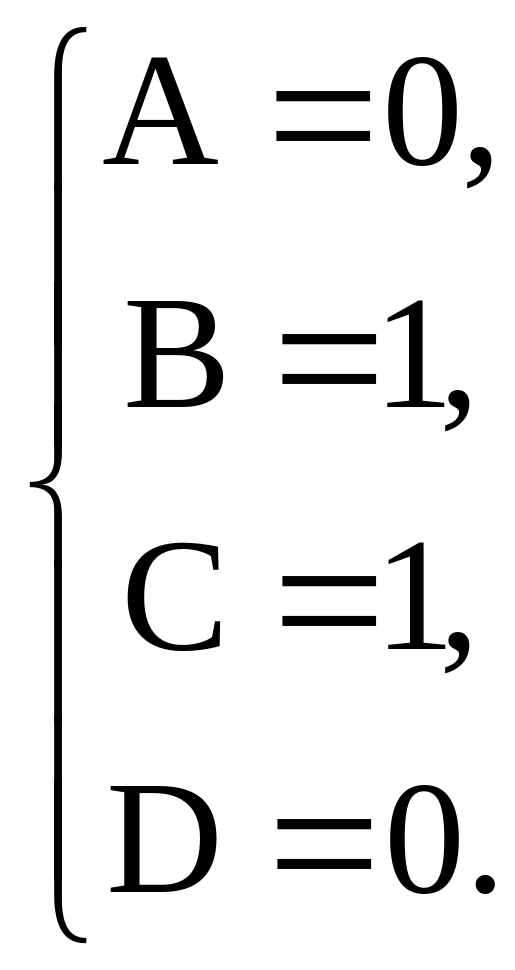
Таким образом,
и общим решением исходного неоднородного уравнения является
Пример 18. Записать вид частного решения линейного неоднородного дифференциального уравнения (без нахождения коэффициентов):
Решение.
a)
Характеристическое уравнение
имеет один корень
кратностью 2. Число
совпадает с этим корнем, поэтому частное
решение
неоднородного уравнения имеет вид
или
б) Характеристическое
уравнение
имеет два простых комплексных взаимно
сопряженных корня:
и
.
Число
совпадает с одним из этих корней, поэтому
частное решение
неоднородного
уравнения следует искать в виде
в)
Характеристическое уравнение
имеет два простых корня: 
Число
не является корнем
характеристического уравнения,
следовательно, частное решение
имеет вид
Теорема 3. Пусть даны два ЛНДУ
,
,
имеющие
частными решениями
и
соответственно.
Тогда
функция
является частным решением уравнения
Пример 19. Найти общее решение уравнения
Решение. Общее решение неоднородного уравнения имеет вид
где – общее решение однородного уравнения
а
– некоторое
частное решение исходного неоднородного
уравнения.
Начнем
с нахождения 
Характеристическое
уравнение
имеет два простых корня:
Таким образом,
Правая
часть исходного уравнения является
суммой двух слагаемых
и
поэтому
можно представить в виде суммы
функций:
где
– частные
решения неоднородных уравнений
, (17)
(18)
соответственно.
Найдем 
Число
является простым корнем характеристического
уравнения, поэтому
или
.
Для нахождения коэффициентов
подставим
в уравнение (17)
Приходим к системе
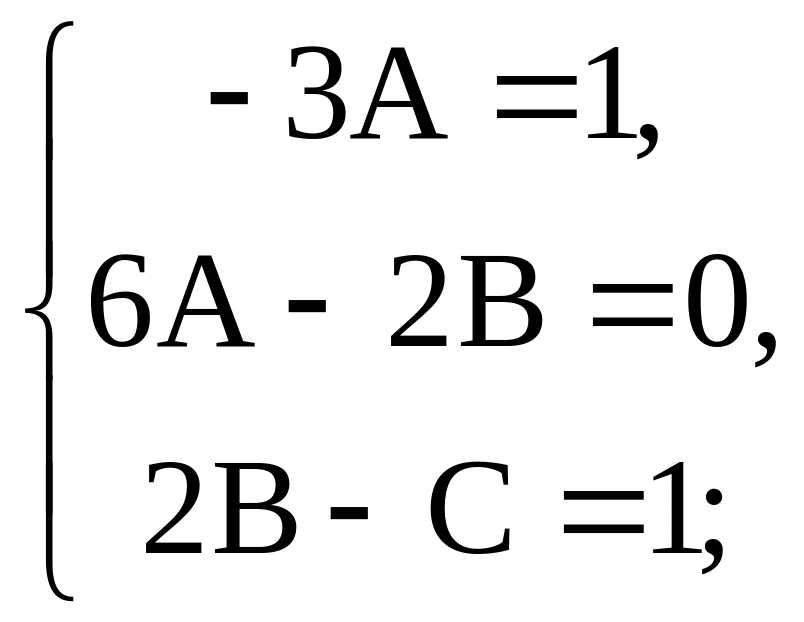
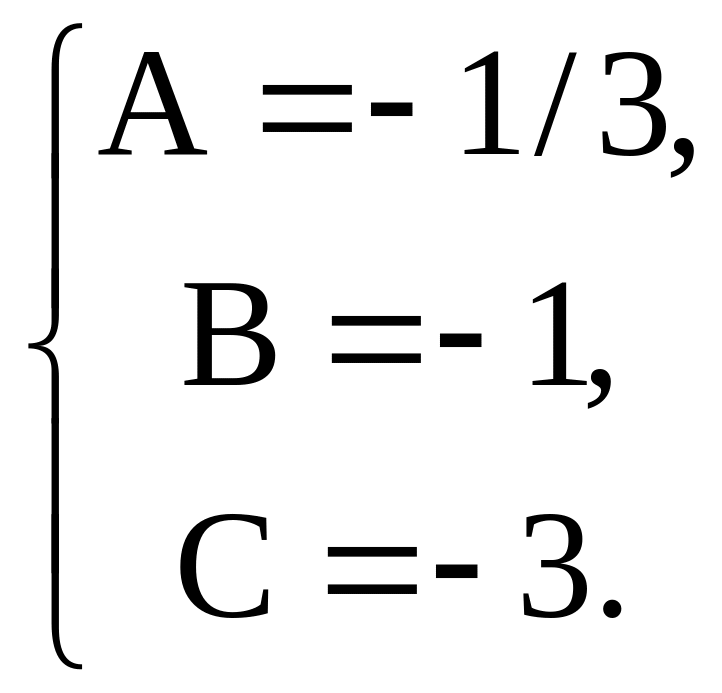
Получим
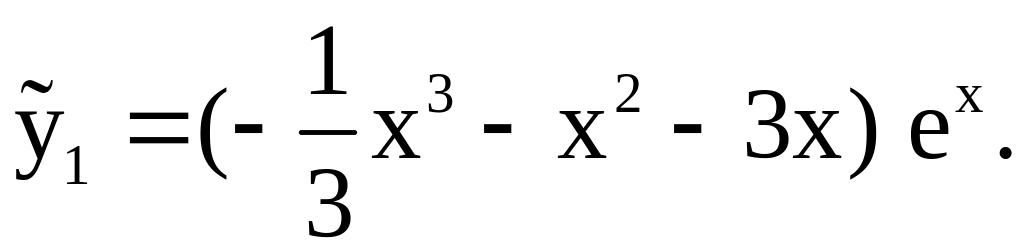
Перейдём
к нахождению
Число
не является корнем характеристического
уравнения, поэтому
будем искать в виде
Имеем
Подставим в (18):
Это равенство приводит к системе
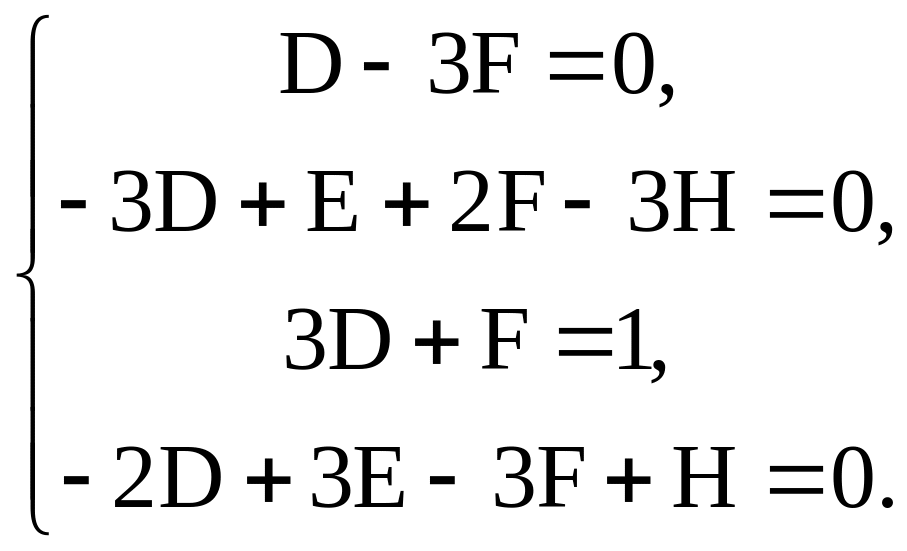
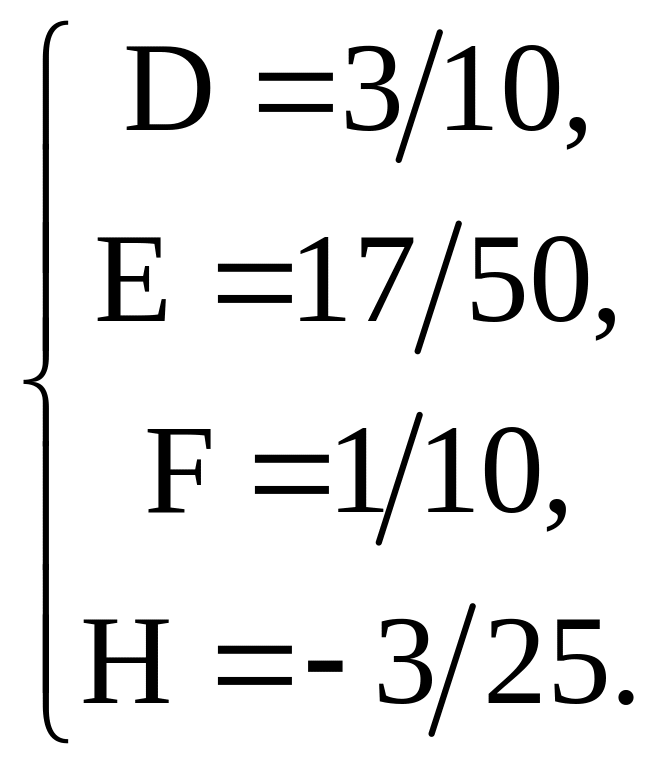
Таким образом,
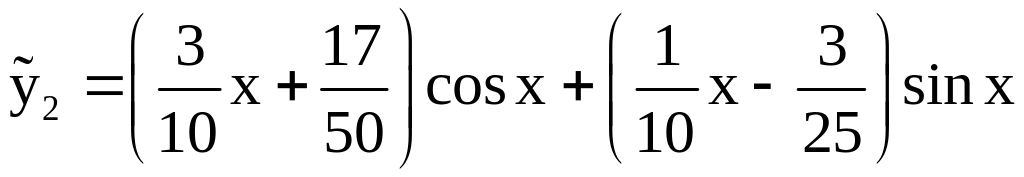
и
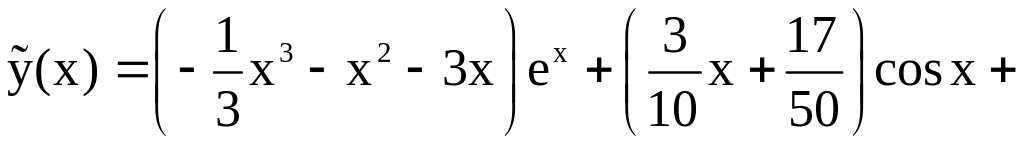
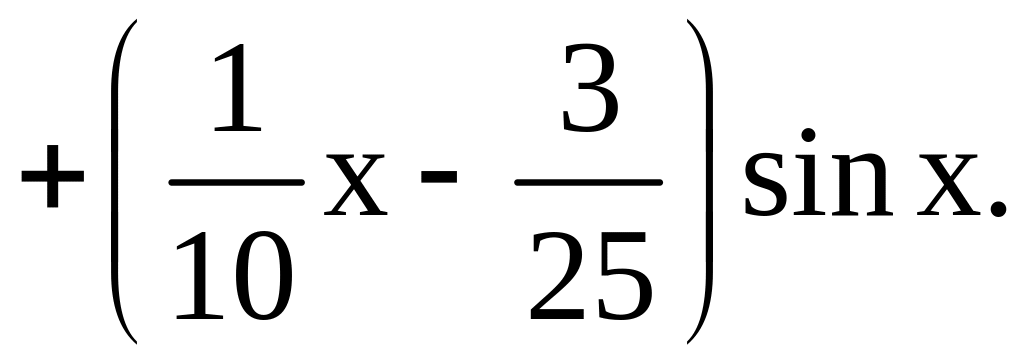
Общим решением нашего уравнения является
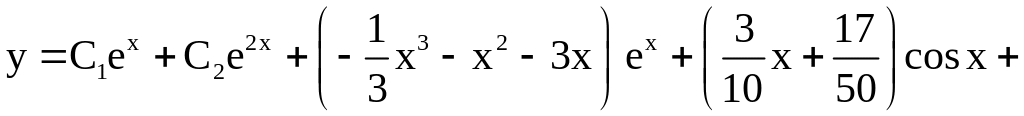
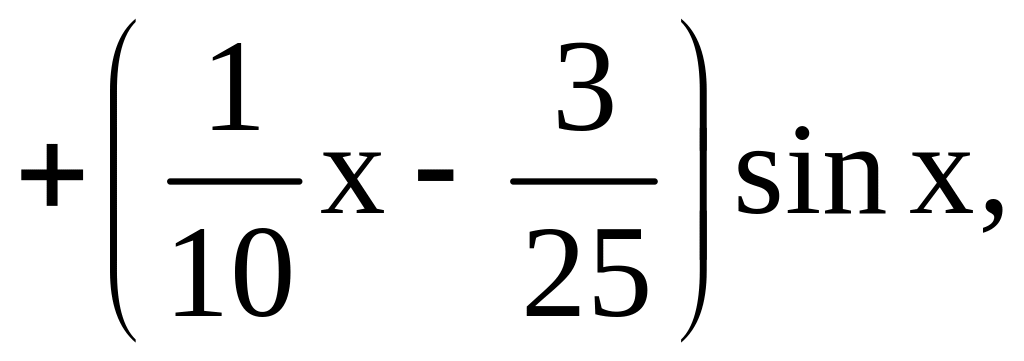
где
–
произвольные постоянные.
Пример 20. Решить задачу Коши
Решение. Сначала
найдем общее решение дифференциального
уравнения. Характеристическое уравнение
имеет два простых вещественных корня
поэтому общим решением соответствующего
однородного уравнения
является
Найдем
частное решение
неоднородного уравнения. Число
не является корнем характеристического
уравнения, поэтому
будем искать в виде
Имеем
Подставим
в исходное дифференциальное уравнение:
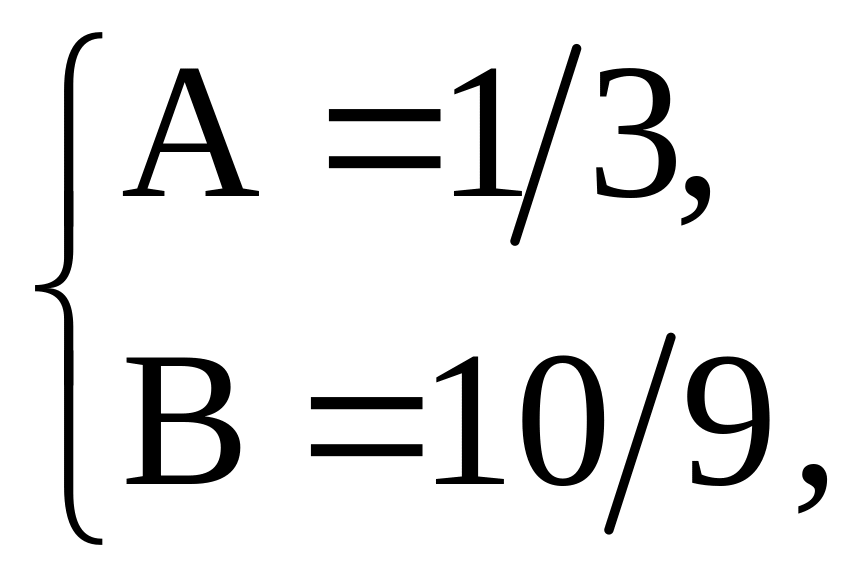
откуда
находим
.
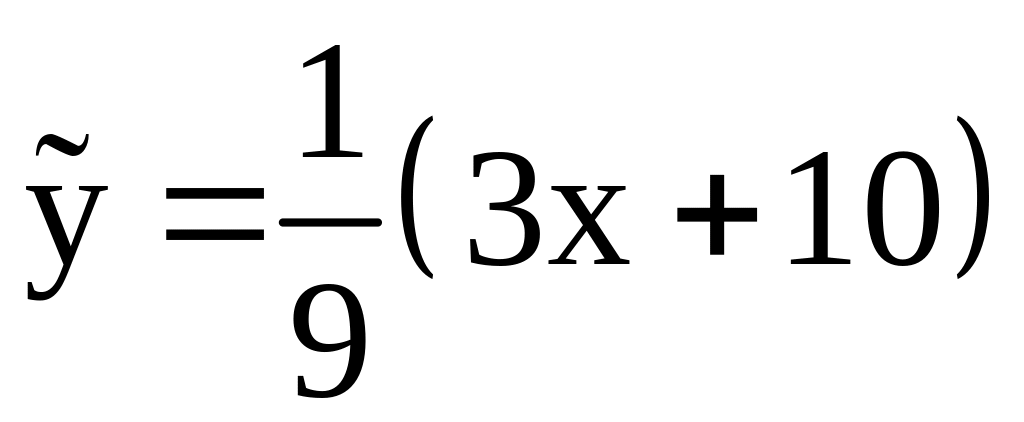Таким
образом, общим решением дифференциального
уравнения является
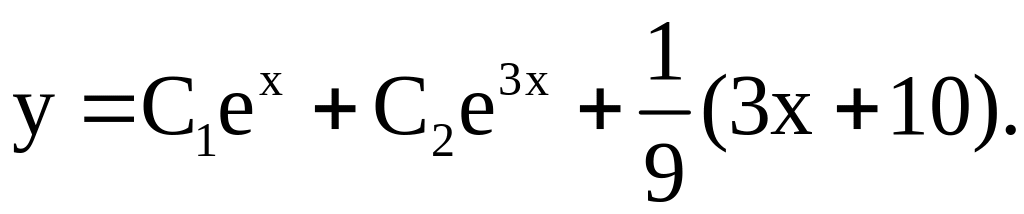
Для
нахождения коэффициентов
воспользуемся начальными условиями
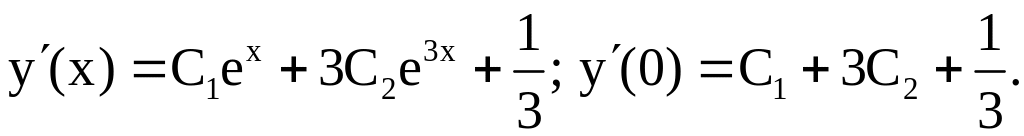
Составим и решим систему уравнений
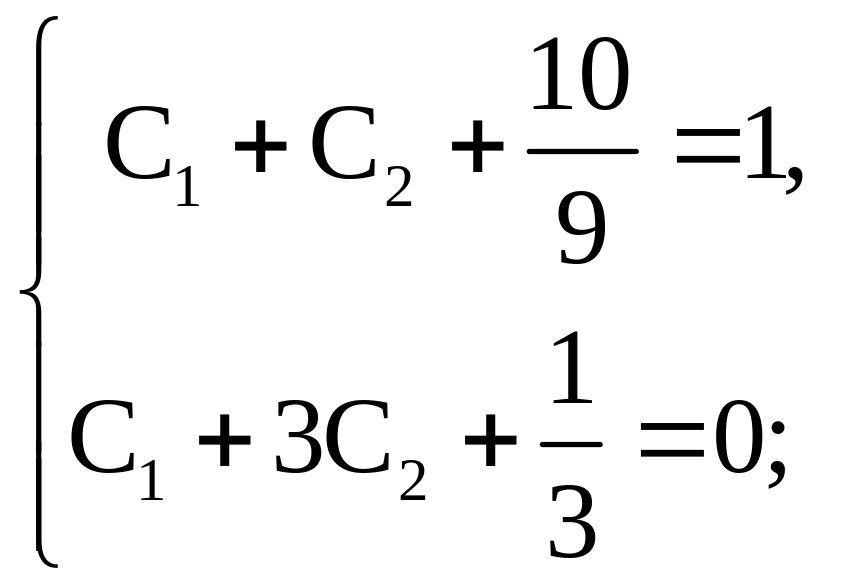
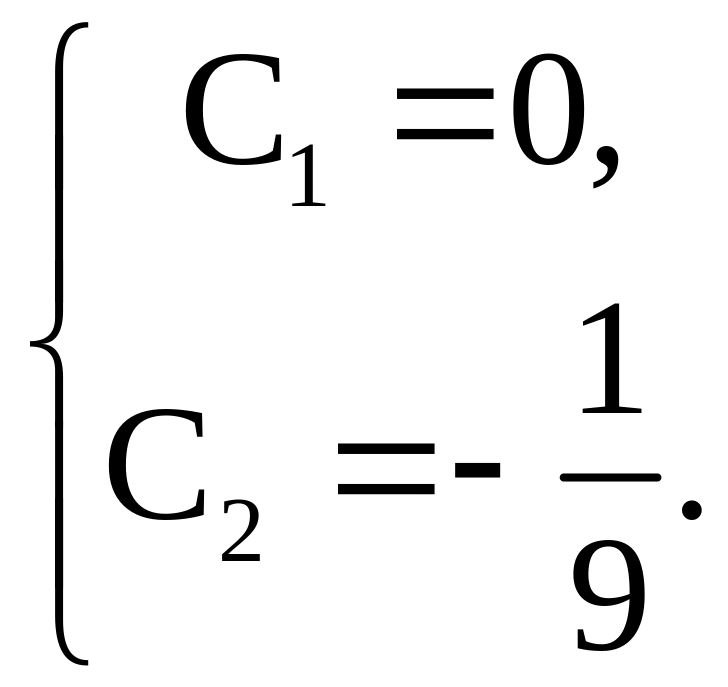
Итак, решением задачи Коши является функция
