Выражденная и невыражденная матрица

ОПРЕДЕЛЕНИЕ: Квадратная матрица называется невырожденной, если ее определитель не равен 0, в противоположном случае называется выражденной

Вычисление определителей произвольных порядков

Для вычисления определителя следует при помощи Элементарных Преобразований с учетом свойств определителей привести определитель к треугольному виду.

Миноры и алгебраические дополнения

Пусть дан определитель порядка n.

(1)

При этом 1≤k≤n-1 => n≥2, где k – кол-во строк.

Выберем в определителе k строк с номерами и k столбцов с номерами 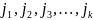. Из элементов стоящих на пересечении выбранных строк и столбцов построим определитель порядка k.

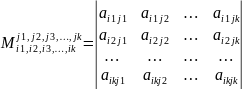
Такой определитель называется минором k-ого порядка.

Отметим, что минор 1-ого порядка 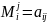, есть элемент определителя с указанными номерами.

Минор порядка n-1, есть определитель порядка n-1 (k=n-1).

Пусть выбраны k строк и k столбцов, вычеркнем эти строки и столбцы, из элементов, не зачёркнутых ни разу, образуем определитель порядка n-k. Этот определитель называется дополнительным минором к этому минору, и обозначается .

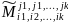Теорема Лапласа

Пусть построен минор 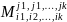. Его алгебраическим дополнением называют число

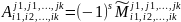
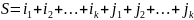
Рассмотрим определитель , выделим и зафиксируем в нём k строк (столбцов), тогда определитель равен сумме всевозможных произведений миноров выбранных строк (столбцов)на их алгебраические дополнения.

Следствие из теоремы Лапласа

1) Определитель равен сумме произведений элементов фиксированной строки (столбца) на их алгебраические дополнения.

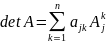
	(2)
	(3)

Разложения (2) и (3) называют разложением определителя по строке с №k (по столбцу с №j).

Формулы (2) и (3) сводят вычисления определителя порядка n к вычислению k определителей порядка n-1. Это позволяет использовать в качестве определения определителя, полагая его известным при n=1.

2) Пусть B = , обозначим, 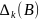, определитель, полученный из определителя (1) заменой столбца с номером k на столбец с номером b.

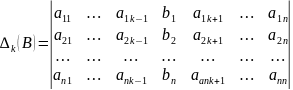
Ясно, что алгебраические дополнения у элементов столбца с номером k, у определителя такие же как и алгебраические дополнения этого столбца у исходного определителя.

Тогда в силу формулы (3) получим, что

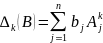(4)

Будем теперь вместо B в полученную формулу подставлять столбцы сходного определителя. Если мы подставим вместо B любой другой столбец с номером, отличным от k, то получим определитель с 2-мя одинаковыми столбцами, который в силу свойств равен 0.

Если же мы подставим с номером совпадающим с номером k, то мы получим исходный определитель.

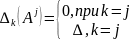(5)

Формулы Крамера

Рассмотрим квадратную СЛАУ

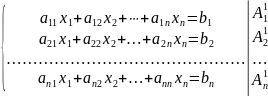
Выполним следующие элементарные преобразования.

(a₁₁ A¹₁ + a₂₁ A²₁ +…+ a_n1 Aⁿ₁ )x₁ + (a₁₂ A¹₁+… +a_n2 A¹_n )x₂ +…+(a_1n A¹₁+….a_nn A¹_n)x_n=b₁ A¹₁+

+b₂ A¹₂+b_n A¹_n

Воспользуемся формулой (5) Аналогичным образом домножая уравнения системы на алгебраические элементы других столбцов аналогичным образом, получаем:

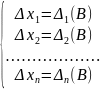(6)