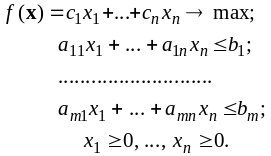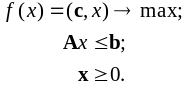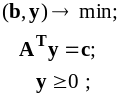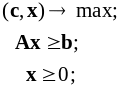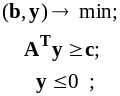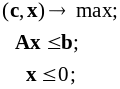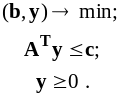27

Министерство общего и профессионального образования

Российской Федерации

Ростовский ордена Трудового Красного Знамени

государственный университет

Л.Н.Землянухина, А.Б.Зинченко,

С.М.Макмак, Л.И.Сантылова

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для студентов дневного и вечернего отделений

механико-математического факультета

по курсу “Методы оптимизации”

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

И СМЕЖНЫЕ ВОПРОСЫ

Часть II

Ростов-на-Дону

1998

Методические указания рекомендованы к печати заседанием

кафедры исследования операций механико-математического

факультета РГУ,

протокол N1 от 2 сентября 1997 г.

ОГЛАВЛЕНИЕ

5.

Теория двойственности . . . . . . . . . . . . . . . . . . . . . . . . . 5.1.Построение двойственной задачи . . . . . . . . . . . . . . . 5.2. Одновременное решение прямой и двойствен­ной задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.3. Исследование решений задач линейного програм­мирования на оптимальность . . . . . . . . . . . . . . . . . 5.4. Двойственный симплекс-метод . . . . . . . . . . . . . . 5.5. Упражнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4 4 8 16 21 28

Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

5. Теория двойственности

В данном разделе рассматривается один из центральных вопросов линейного программирования - теория двойственности. С каждой задачей линейного программирования, которую будем называть исходной или прямой, можно связать некоторую другую линейную задачу, называемую двойственной. Совместное рассмотрение таких задач, составляющих единую двойственную пару, оказывается весьма эффективным средством при построении численных методов линейного программирования и при экономическом анализе результатов расчета.

5.1.Построение двой­ствен­ной задачи.

Рассмотрим задачу линейного программирования в стандартной форме. Назовем ее прямой.

или

(1)

Двойственной к задаче (1) называется следующая задача :

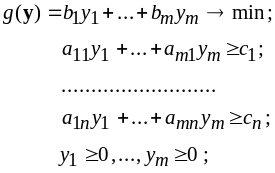
или

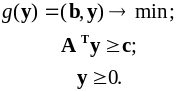
(2)

Эти задачи образуют взаимно двойственную пару, так как двойствен­ной к задаче (2) является задача (1).

Правила построения двойственной задачи (2):

1) -ому ограничению прямой задачи соответствует -ая неотрицательная двойственная переменная ; неотрицательной прямой переменной соответствует -ое ограничение двойственной задачи типа « »;

2) коэффициентами целевой функции двойственной задачи являются свободные члены ограничений прямой задачи; максимизация целевой функции прямой задачи заменяется минимизацией целевой функции двойственной;

3) матрицей ограничений двойственной задачи служит матрица , получаемая транспонированием ;

4. свободными членами двойственной задачи являются коэффициенты

целевой функции прямой задачи.

Построим двойственные задачи для других форм задач ЛП, используя вве­денное определение и правила преобразования задач ЛП:

п р я м а я д в о й с т в е н н а я

1)

2)

3)

4)

Приведем общую схему построения взаимно двойственной пары задач, где - -ый столбец , - -ая строка матрицы :

п р я м а я д в о й с т в е н н а я

,				,
,
,				,
,				,
	,				,
	,				,
	,				.

Рассмотрим построения двойственных задач на примере.

Пример 1. Даны прямые задачи. Построить двойственные к ним задачи, используя общую схему построения и взаимную двойственность задач.

a)

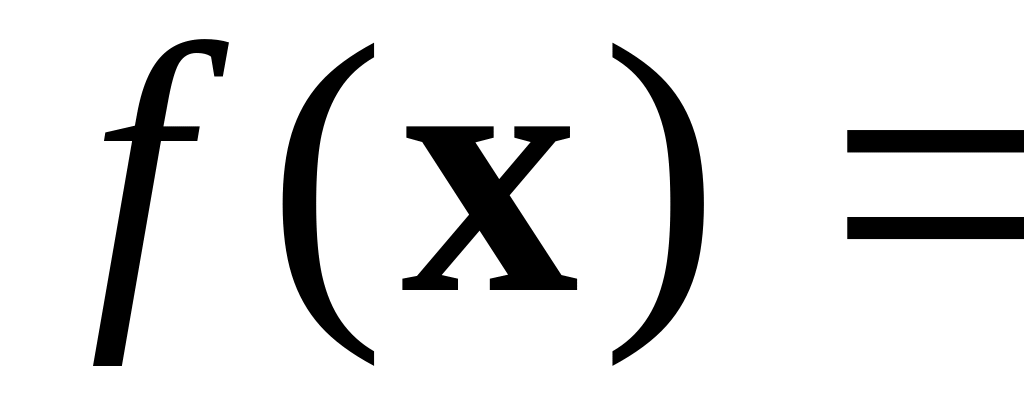
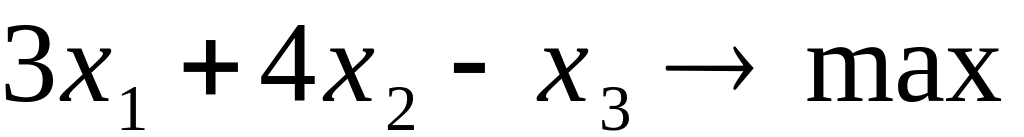
			двойственные переменные
		

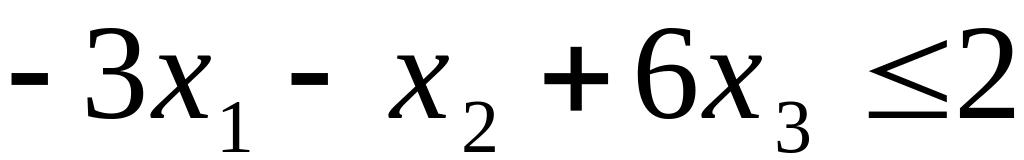
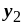
Вводим вектор двойственных переменных по числу ограничений прямой задачи. Тогда двойственная задача имеет вид:

b)

	

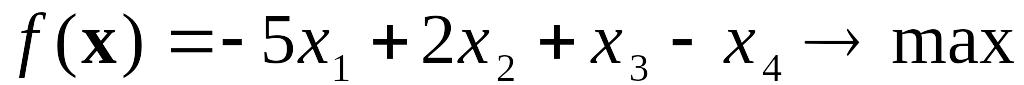
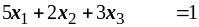
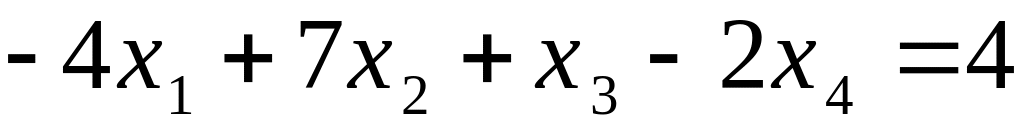
Соответствующая двойственная задача запишется в виде:

В этом примере вектор двойственных переменных имеет раз­мерность 3. Исходная задача дана в канонической форме, следовательно, все двойственные переменные - свободные.

в)

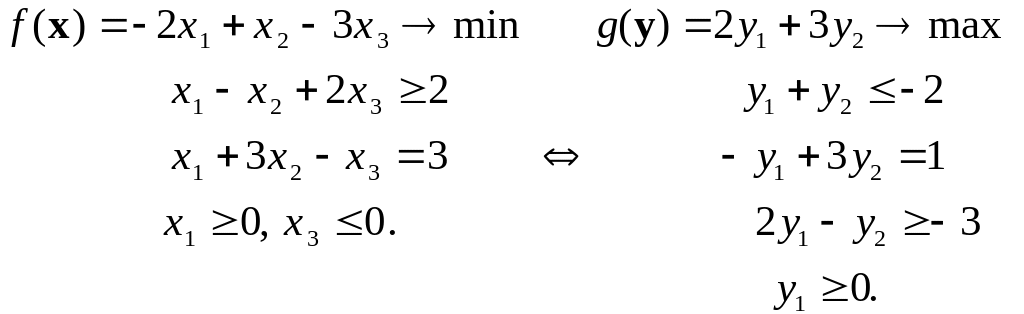
-вектор двойственных переменных, при этом соответствует ог­раничению-неравенству типа « », а соответствует ограничению-ра­вен­ст­ву и является свободной. Неотрица­тель­­ной переменной соот­вет­ст­вует первое ограничение, а свободной - второе ограничение-равенство двой­ст­вен­ной задачи. Переменная неположительная, поэтому ей соответ­ствует­ огра­ничение типа « » . Так как прямая задача является задачей ми­­­ни­ми­зации, то двойственная задача есть задача на максимум.