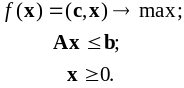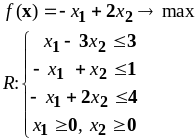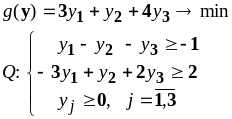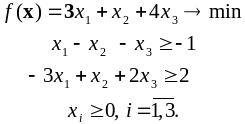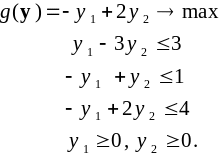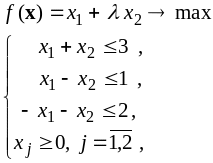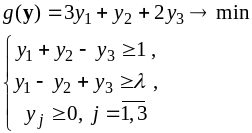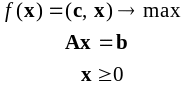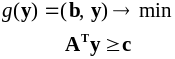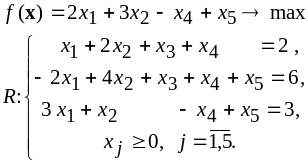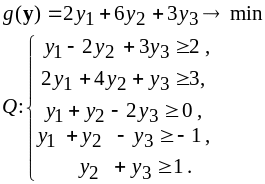5.3. Исследование решений задач линейного
ПРОГРАММИРОВАНИЯ НА ОПТИМАЛЬНОСТЬ
Схема проверки решения на оптимальность основана на использовании 2-ой теоремы двойственности.
2 теорема
двойственности.
Для того, чтобы допустимые решения
![]() прямой и двойственной задач
прямой и двойственной задач
|
и |
|
были оптимальными, необходимо и достаточно, чтобы выполнялись условия:
(1) если
![]() ,
то
,
то
![]() ;
;
(2) если
![]() ,
то
,
то
![]() ; (6)
; (6)
если
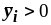 ,
то
,
то
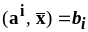 ;
;если
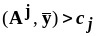 ,
то
,
то
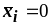 ,
,
где - -ый столбец , - -ая строка матрицы .
Эта теорема позволяет установить оптимальность допустимого решения одной задачи на основании анализа системы линейных уравнений, полученных из соотношений (1)-(4) формул (6).
Схема
проверки на оптимальность допустимого
решения
![]() прямой задачи:
прямой задачи:
1)
построить множества
![]() ;
;
2) построить систему уравнений относительно двойственных переменных из условий (6)
![]() (7)
(7)
3) если система (7) противоречива, то план не является оптимальным, иначе проверить, есть ли среди решений системы (7) допустимые решения двойственной задачи; если проверка завершится обнаружением допустимых решений двойственной задачи, то - оптимальное решение прямой задачи, и иначе не является оптимальным.
Пример 7.
Проверить на оптимальность решения
![]() и
и
![]() следующей задачи ЛП (прямая):
следующей задачи ЛП (прямая):
Прямая задача: |
|
Двойственная задача: |
|
|
|
а)
исследуем на оптимальность решение
![]() .
Строим множества
.
Строим множества
![]() и систему уравнений (6):
и систему уравнений (6):
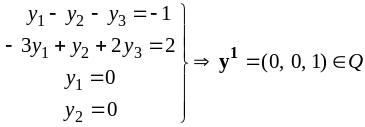
Таким
образом,
-
оптимальное решение прямой задачи, а
![]() - оптимальной решение двойственной;
- оптимальной решение двойственной;
б)
Проверим теперь на оптимальность решение
![]() .
Следует заметить, что в этом случае
достаточно сравнить значения функций
.
Следует заметить, что в этом случае
достаточно сравнить значения функций
![]() и сделать вывод, однако проведем
исследование с помощью предложенной
схемы. Строим множества
и сделать вывод, однако проведем
исследование с помощью предложенной
схемы. Строим множества
![]() и систему уравнений (6):
и систему уравнений (6):
![]() .
.
Но
![]() ,
так как
,
так как
![]() .
Следовательно,
.
Следовательно,
![]() не является оптимальным решением
исходной задачи.
не является оптимальным решением
исходной задачи.
▀
Пример 8.
Проверить на оптимальность решение
![]() следующей задачи:
следующей задачи:
Прямая задача: |
|
Двойственная задача: |
|
|
|
Выпишем
условия (6), учитывая, что
![]() :
:
![]() .
.
Выясним,
есть ли среди полученных решений
допустимые решения двойственной задачи.
Для этого подставим найденное решение
в 1-ое и 2-ое ограничения и в условия
![]() двойственной задачи:
двойственной задачи:
|
|
|
|
|
Последняя система не противоречива, поэтому решение является оптимальным.
▀
Пpимеp 9.
Найти значения параметра
![]() ,
при котором решение
,
при котором решение
![]() является оптимальным решением прямой
задачи:
является оптимальным решением прямой
задачи:
Прямая задача: |
|
Двойственная задача: |
|
|
|
Выписываем
условия (6) (![]() )
:
)
:
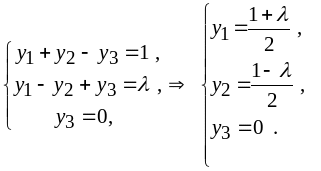
Проверим,
существуют ли допустимые решения
двойственной задачи среди найденных
и при каких значениях
![]() .
Подставим полученные решения
в те ограничения двойственной задачи,
которые не использовались при
построении условий (6). Получим:
.
Подставим полученные решения
в те ограничения двойственной задачи,
которые не использовались при
построении условий (6). Получим:
![]()
Итак,
для
![]() решение
является оптимальным решением прямой
задачи.
решение
является оптимальным решением прямой
задачи.
▀
З а м е ч а н и е. Для задач в канонической фоpме и двойственных к ним
|
|
условия оптимальности имеют вид 1), 4) формул (6):
если
![]() ,
то
,
то
![]() ;
;
(7)
если
![]() , то
, то
![]() .
.
Пpимеp 10.
Пpовеpить, является ли допустимое решение
![]() прямой задачи линейного программирования
оптимальным решением:
прямой задачи линейного программирования
оптимальным решением:
Прямая задача: |
|
Двойственная задача: |
|
|
|
Выпишем условия (7):
![]()
Подставляем найденное решение в 1-ое, 3-е и 4-ое ограничения двойственной задачи:
![]()
Итак
- оптимальное решение прямой задачи, а
![]() - оптимальные решения двойственной
задачи.
- оптимальные решения двойственной
задачи.
▀