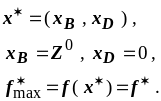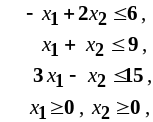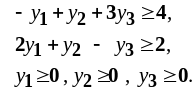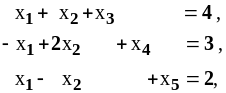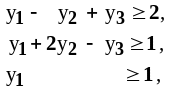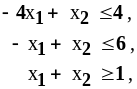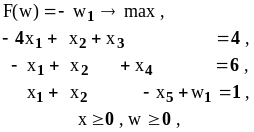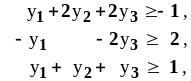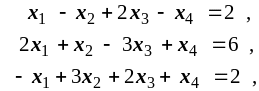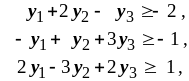5.2. Одновременное решение прямой и двойственной задач

Одновременное решение прямой и двойственной задач основано на испо­льзовании теорем двойственности. В данном разделе рассмотрен вопрос построения оптимального плана двойственной задачи, если известна оптимальная симплекс-таблица прямой задачи.

Лемма. Пусть дана взаимно двойственная пара задач и пусть и допустимые решения этих задач. Тогда . Если , то и - оптимальные решения.

1-я теорема двойственности. Если одна из задач взаимно двойственной пары разрешима, то разрешима и другая задача, при этом оптимальные значения целевых функций совпадают. Если целевая функция одной из задач не ограничена (сверху - для задачи максимизации, снизу - для задачи минимизации), то множество допустимых планов другой задачи пусто.

Из этой теоремы вытекает следующее

Следствие. Для того, чтобы допустимые решения и двойственной па­ры задач были оптимальны, необходимо и достаточно, чтобы значения целевых функций на этих планах совпадали:. .

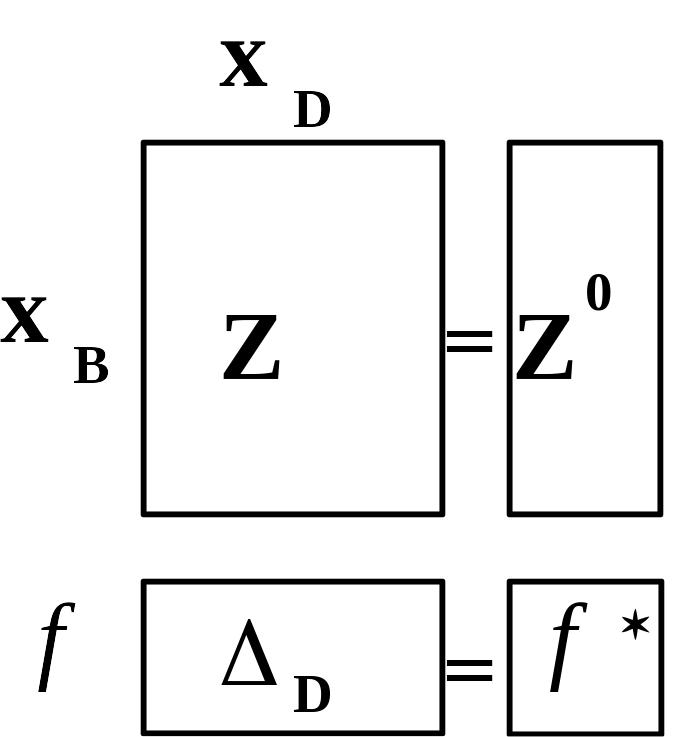
На основании первой теоремы двойственности и основных формул симп­лекс метода может быть предложена следующая схема одновременного решения прямой и двойственной задач. Рассмотрим вза­­имно двойственную пару задач (3) :



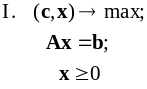
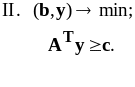
Решим прямую задачу симплекс-методом. Тогда либо задача I ока­­жет­ся не­раз­решимой и согласно 1-ой теореме двойственности неразрешима и двой­ствен­ная задача, либо будет построена оптимальная симплекс-таблица T , опти­маль­­ный базис и оптимальное опорное решение . Пусть оптимальная симплекс-таблица имеет вид:

T (симплекс-таблица):		Оптимальное решение:

Используя симплекс-таблицу и полученное опорное реше­ние, можно пос­троить оптимальное опорное решение двойственной задачи двумя спосо­бами.

1 способ. Воспользуемся формулой для вычисления относитель­­­­­ных оценок через оптимальное решение двойственной задачи:

, (4)

при этом, если - базисная переменная, то , иначе находится в -строке таблицы T. Если матрица содержит единичных ортов-сто­л­бцов , то (4) принимает вид откуда, при этом .

Если же не содержит полный набор единичных столбцов, то выбираем линейно независимых столбцов и решаем систему линейных уравнений относительно : .

2 способ. Для вычисления воспользуемся формулой :

(5)

что приводит к решению системы . Однако, если матрица содержит полный набор единичных столбцов , то мат­ри­ца

строится с помощью таблицы по правилам : если переменная - небазисная, то ; если - базисная , то .

Пример 2. Решить одновременно прямую и двойственную задачи:

Прямая задача					Двойственная задача

Решим прямую задачу симплекс-методом, предварительно приведя ее к кано­ни­ческому виду; для этого используем дополнительные неотрицательные пе­ременные .

						4	2
			0			-1	2	=	6
			0			1	1		9
			0			3	-1		15
								=
						-4	-2	=	0

1/3

5/3

=

11

3/4

-5/4

=

6

-1/3

4/3

=

4

-1/4

3/4

=

3

1/3

-1/3

=

5

1/4

1/4

=

6

4/3

-10/3

=

20

1/2

5/2

=

30

Так как относительные оценки в - строке последней симплекс-таблицы не­отрицательны, то таблица оптимальная, - оп­ти­маль­ное решение

пря­мой задачи, . Перейдем к рас­смот­рению двойс­т­вен­ной задачи. Из разрешимости прямой задачи выте­ка­ет разрешимость двойственной и ра­венство оптимальных значений целевых функций этих за­­дач: . Построим оптимальное ре­ше­ние двойственной задачи.

1 способ. Матpица ограничений прямой задачи имеет полный набор еди­ничных столбцов поэтому в формуле (4) ис­пользуем относительные оценки Полу­чаем - оптимальное решение двойственной за­да­чи.

2 способ. Рассмотрим базис оптимального плана

.

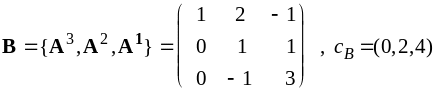Находим обратную матрицу , используя тот факт, что столбцы единичные, переменные - небазисные, - базисная в оп­тимальной симплекс-таблице. Имеем

▀

Пpимеp 3. Решить прямую и двойственную задачи:

Прямая задача				Двойственная задача

Решаем прямую задачу симплекс-методом:

				2	1
	1			1	1		=	4				2	-1		=	1
	-1			-1	1		=	3				-1	1		=	3
	2			1	-1		=	2				0	1		=	5
				2	-3		=	5				-1	3			14

				1/2	-1/2		=	1/2		Итак, прямая задача разре­ши­ма:
				1/2	1/2		=	7/2		,
				0	1		=	5		,
				1/2	5/2		=	29/2		сле­­­довательно, разрешима и

двойственная задача, причем .На­хо­дим оптимальное решение двойственной задачи, используя формулы (4). Полагаем (номера единичных столбцов мат­ри­цы ограничений). Имеем -оптимальное решение двойственной за­да­чи. ▀

Пpимеp 4. Pешить пpямую и двойственную задачи

			

Приведем к каноническому виду прямую задачу и решим ее симплекс-методом, используя для построения начальной симплекс-таблицы метод искусственного базиса.

	Каноническая форма прямой задачи :															Вспомогательная зада­ча
												
																			1	0
					-4	1	0		=	4				0					5	-4		=	8
					-1	1	0		=	6				0					2	-1		=	7
					1	1	-1		=	1				1					1	-1		=	1
					-1	-1	1		=	-1									0	0		=	0
																			0	-1		=	1

Последняя таблица дает начальный опорный план прямой задачи и начальную симплекс-таблицу, из которой получаем, что прямая задача неразрешима, т.к. целевая функция не ограничена сверху на множестве допустимых планов. Следовательно неразрешима и двойственная, множество ее допустимых планов пусто. ▀

Пpимеp 5. Решить прямую и двойственную задачи:

Прямая задача				Двойственная задача

Приведем исходную задачу к каноническому виду и решим симп­лекс-методом, используя для построения начальной симплекс-таб­ли­цы метод искусственного базиса. Имеем:

Вспомогательная задача
				1	-1	1	0	0		=	4
				2	0	1	-1	0		=	6
				2	-2	1	0	-1		=	1
				-5	3	-3	1	1			-11

			-1	1	0	1		=	3				-1	1	0		=	3
			0	2	-1	1		=	5				1	1	-1		=	2
			2	-2	0	-1		=	1				1	-1	0		=	4
			1	-3	1	-2		=	-8				-1	-1	1			-2

				-1	-1
	1			-2	1		=	1				-2	1		=	1
	2			1	-1		=	2				-1	1		=	3
	1			2	-1		=	6				0	1		=	7
				0	0		=	0				1	1			12
				3	-1		=	11

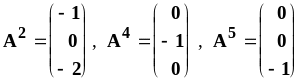Оптимальный план прямой задачи . Оп­ти­мальное решение двойственной задачи строим, используя соот­ношения (4). Полагаем , так как столбцы линейно независимы.

Для определения строим систему линейных уравнений :

▀

Пpимеp 6. Решить прямую и двойственную задачи:

Прямая задача				Двойственная задача

Приведем исходную задачу к каноническому виду и решим симп­лекс-методом, используя для построения начальной симплекс-таб­ли­цы метод искусственного базиса. Имеем:

Вспомогательная задача
				1	-1	2	-1		=	2
				2	1	-3	1		=	6
				-1	3	2	1		=	2
				-2	-3	-1	-1			-10

			0	2	4		=	4				2	4		=	4
			3	-2	-5		=	4				-2/3	-5/3		=	4/3
			-1	3	2		=	2				7/3	1/3		=	10/3
			-3	0	1		=	-8				-2	-4			-4

				-1
	1			1/2		=	1		Оптимальный план прямой задачи:
	-2			1/6		=	3
	1			13/6		=	3		Оп­ти­мальное решение двойственной
				0		=	0		задачи строим, используя соот-­
				10/3			-2		ношения (4) при , так

как столбцы линейно независимы:

▀