Первый критерий обратимости матрицы

ТЕОРЕМА: Квадратная матрица А обратима тогда и только тогда, когда она представима в виде произведения элементарных матриц.

ДОКОЗАТЕЛЬСТВО:

Необходимость: Если матрица А обратима то в силу лемма r=n и в равенстве А=ВDrС Dr является единичной матрицей, поэтому А=ВС. По построению каждая их матриц В и С является произведением элементарных матриц.

Достаточность: Если А является произведением элементарных матриц, то она обратима как произведение обратимых матриц.

Второй критерий обратимости матрицы

Пусть А ϵ M_mxn (|R).

Назовем матрицу вида Dr эквивалентной матрицы А, если она получена из матрицы А, при помощи элементарных преобразований (А~Dr)

Пусть А~Dr. Рангом матрицы А называют число r=rang A (rack A) можно показать, что число r определяется корректно в том смысле что он не зависит от элементарных преобразований приводящих матрицу А к виду Dr.

ТЕОРЕМА: Матрица А обратима тогда и только тогда когда ее ранк совпадает с порядком

rang A = n

ДОКОЗАТЕЛЬСТВО: Если rang A=n => r=n. Обратно если матрица А обратима, то она представима в силу первого критерия в виде произведения элементарных матриц. А=Е₁…Е_р Это равенство можно рассматривать как равенство в котором А=Е₁…Е_р*Еn*Еn , (Е₁…Е_р=В, Еn=С) но тогда Dr=Еr=> r=n, что равносильно rangA=n.

Третий критерий обратимости матрицы

Матрицы А и В называются делителями нуля, если А и В = 0. При этом они являются нетривиальными делителями нуля, если А≠0 и В≠0. При этом они являются нетривиальными делителями нуля, если А≠0 и В≠0.

ТЕОРЕМА: Матрица А является обратимой тогда и только тогда, когда она не является нетривиальными делителями нуля.

ДОКОЗАТЕЛЬСТВО:

Необходимость: Предположим, что матрица А обратима, но вопреки утверждению является нетривиальными делителями нуля. Это значит:

А^-1А=En, AA^-1=En, B≠0 : BA=0, B(AA^-1)=0*A^-1, B=0

Достаточность: Предположим, что матрица А необратима, но не является нетривиальным делителем нуля. Рассмотрим равенство А=ВDrС. Поскольку матрица А – необратима, матрица Dr, тоже необратима. Значит матрица Dr*≠0. Рассмотрим матрицу G=C^-1Dr*B^-1≠0. Найдем

АG=BDr(CC^-1)Dr*B^-1=BDrDr*B^-1=B0B^-1=0, таким образом матрица А является нетривиальным делителем нуля, что противоречит предпосылки.

Конструктивное представление разложения матрицы на произведение простейших. Поскольку каждое строчное (столбцовое) элементарное преобразование равносильно умножению на соответствующую элементарную матрица слева (справа) то процедуру приведения матрицы А к виду Dr схематически можно представить так:

А ϵ M_mxn (|R)

СЛЕДСТВИЕ: В частности если матрица А квадратная и обратимая, то выполняя только преобразования строк мы получим схему: (A|En) (En|A^-1), а если выполнять преобразования столбцов, то: .

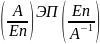Слау Определение и классификация систем линейных алгебраических уравнений

СЛАУ – называют систему уравнений вида:

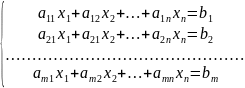(1)

Где: a_kj известные числа называемые коэффициентами системы (1)

b_k известные числа называемые правыми частями системы (1)

x_j неизвестные числа которые подлежат определению из системы (1)

О системе содержащей m уравнений и n неизвестных мы будем говорить, что рассматриваемая СЛАУ mxn.

Если m=n система называется квадратной, и число n называется порядком системы.

Решением системы (1) назовем набор неизвестных x₁, x₂,…,x_n подстановка которых в каждое уравнение системы (1) обращает их в тождество.

Замечание: Когда число неизвестных невелико на ряду x₁, x₂,…,x_n используем x, y, z….