3)Транспанорование

Пусть АϵM_mxn (|R) транспонированную к ней матрицу назовем матрицей А^τ размером M_nxm (|R) каждый элемент которой, есть элемент матрицы А в котором номер строки, есть номер столбца и наоборот. Пример:

А=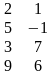 А^τ=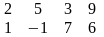

Свойства:

1) Для любой матрицы А имеет место равенство: (А^τ)^τ=А

2) (А+В)^τ=А^τ+В^τ

3) (λА)^τ=λА^τ

4)0^τ=0

5)(Е_n)^τ= Е_n

Замечания:

1)Матрицы для которых имеет место равенство А^τ=А, называют симметричными. Матрица квадратная, и элементы относительно главной диагонали равны.

2)Для квадратных матриц операцию транспонирования можно интерпретировать как порот элементов матрицы на 180^о.

Арифметические векторы

Арифметическим вектором длины n называют упорядоченный набор n чисел

а= (а₁₁, а₂₂,…,а_nn)

а=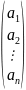 , a_nϵ|R

Арифметический вектор можно рассматривать как частный случай матрицы:

а^τ ϵM_mxn (|R) и а^τ ϵM_mxn (|R)

Это означает, что для арифметических векторов определены линейные операции.

Скалярным произведением двух арифметических векторов называют сумму произведений одноименных координат этих векторов.

ab= a*b^τ=a^τ*b=a^τ*b^τ=a₁b₁+a₂b₂+…+a_nb_n

Свойства скалярного произведения

1) Скалярное произведение престановочно. а*b^τ=b*a^τ

2) Скалярный сомножитель можно относить к любому сомножителю скалярного произведения. λ(a*b^τ)=(λa)*b^τ=a*(λb^τ)

3) Скалярное произведение дистрибутивно (распределительно) относительно каждого аргумента (сомножителя). (a₁+a₂)*b^τ=a₁b^τ+a₂b^τ;

4) Скалярный квадрат неотрицателен, и равен нулю тогда и только тогда, когда равен нулю арифметический вектор. a²=а*а>=0 и а²=0<=>a=0

Умножение матриц

Пусть АϵM_mxn (|R) ; ВϵM_mxn (|R) есть арифметический вектор длины n. Ясно что столбцы это арифметические векторы длины n.

Произведение матрицы АϵM_mxn (|R) на матрицу ВϵM_mxn (|R) называют матрицу АВϵM_mxn (|R) каждый элемент которой, есть скалярное произведение строки матрицы А на столбец матрицы В с соответствующими номерами. (А*В)=А_к*Вⁱ

Свойства умножения матриц

1) Произведение матриц не обладает свойством коммутативности в том смысле что, даже если оба произведения определены А*В и В*А и имеют одинаковые размеры, они различны.

А*В≠В*А

Матрицы А*В=В*А называются перестановочными и коммутирующими.

λ(А*В)=(λА)*В=А*(λВ)

3) Операция умножения матриц дистрибутивна относительно по любому аргументу.

(А₁+А₂)*В=А₁В+А₂В; А(В₁+В₂)=А*В₁+А₁*В₂

Доказательство:

А₁,А₂ ϵ M_mxn (|R); ВϵM_mxn (|R);

А₁+А₂ ϵ M_mxn (|R); (А₁+А₂)*В ϵ M_mxn (|R);

А₁*В ϵ M_mxn (|R); А₂*В ϵ M_mxn (|R);

А₁В+А₂В ϵ M_mxn (|R);

[(A₁+A₂)B]_kj=(A₁+A₂)_KB^j=((A₁)_K+(A₂)_K)*B^j=(A₁)_K*B^j+(A₂)_K*B^j=(A₁B)_kj+(A₂B)_kj

4) (A*B)^τ=B^τ*A^τ

5) А ϵ M_mxn (|R); E_mA=A, A*E_n=A

Замечание: Если матрица А квадратная то выполняется оба равенства А*Е_n=E_nA=A

6) А ϵ M_mxn (|R); В ϵ M_mxn (|R); С ϵ M_mxn (|R), тогда имеет место быть равенство: (А*В)*С=А*(В*С)

Понятие об обратной матрице

Пусть А ϵ M_mxn (|R). Будем говорить, что эта матрица обратима, если найдется такая квадратная матрица В такого же порядка, так что АВ=Е_n, ВА=Е_n

Если матрица А обратима то матрица В называется обратимой к ней, В=А^-1

Свойства:

1) Если матрица А обратима, то и обратная к ней матрица А^-1 обратима и при этом (А^-1)^-1=А;

(А^-1А=Е_n; АА^-1=Е_n)

2)Если матрица А, В обратимы, то и обратимо их произведение, при этом (АВ)^-1=В^-1А^-1

Доказательство:

(АВ)(В^-1А^-1)=А(ВВ^-1)А^-1=(АЕ_n)А^-1=Е_n; (В^-1А^-1)(АВ)=В^-1(А^-1А)В=В^-1(Е_nВ)=В^-1В=Е_n

3) Если матрица А обратима, то и транспонированная к ней матрица тоже обратима, при этом

(А^τ)^-1=(А^-1)^τ

Доказательство:

(АВ)^τ=В^τА^τ т.к. А^τ(А^-1)^τ=(А^-1А)^τ=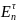 =E_n

4) Единичная матрица любого порядка обратима и при этом (Е_n)^-1=E_n

5) Нулевая матрица любого порядка необратима.

Замечание: Существуют и не нулевые обратимые матрицы А= -необратима. Если допустить, что существует матрица В=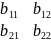 следовательно АВ=Е₂, ВА=Е₂

b₁₁+b₁₂=1

b₁₂+b₂₂=0 следовательно что не существует такой матрицы В

b₁₁+b₂₁=0

Определение: Множество квадратных матриц порядка n которые являются обратимыми, будем называть группой обратимых матриц порядка n, GϵM_n(|R)