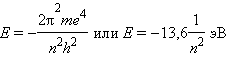14. Квантовое движение в центральном поле. Состояния электрона в поле ядра. Атом водорода и водородоподобные ионы. Квантовые числа.

 Решение уравнения Шредингера для водородоподобного атома имеет фундаментальное значение, т.к. получаемые здесь результаты служат основой для изучения многоэлектронных систем.

Разделение переменных в сферической системе координат

Водородоподобный атом содержит одно ядро и один электрон. Заряд электрона равен -е, заряд ядра +Zе, где Z - порядковый номер элемента. Потенциальная энергия этой системы двух частиц является функцией только расстояния между ними и выражается энергией кулоновского притяжения

(1)Гамильтониан системы запишется в виде 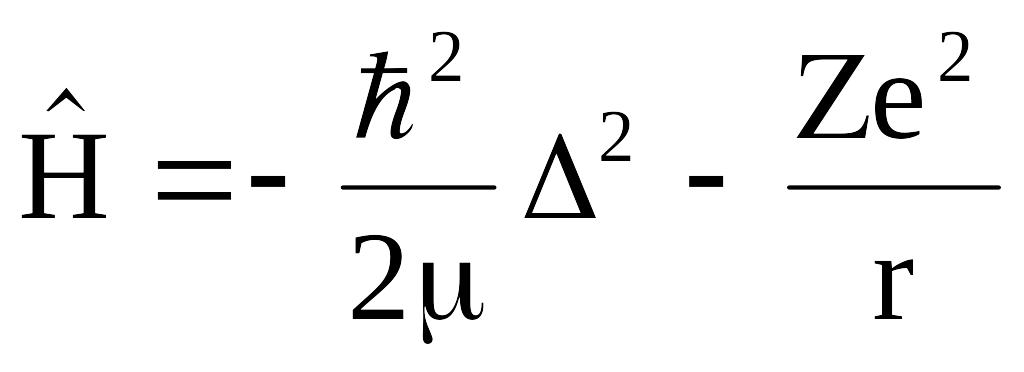(2)

для решения уравнения Шредингера (3)

целесообразно выразить его в сферических координатах, используя оператор Лапласа, преобразованный к сферической системе координат Подставляя его в (3) и переходя к y (r, q, j), имеем:

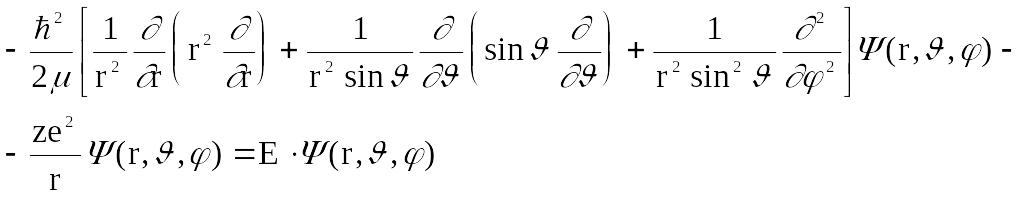(4)

Это дифференциальное уравнение в частных производных второго порядка удобно решить, разделяя переменные. Для этого будем искать его решение в виде = R(r)· (5)

Разделяя переменные в уравнении Шредингера в сферических координатах, получили три уравнения, каждое из которых зависит от одной лишь переменной: это

Ф-уравнение (6)

R- уравнение: (7)

и - уравнение:  

Нормированная функция ( ), таким образом, имеет вид

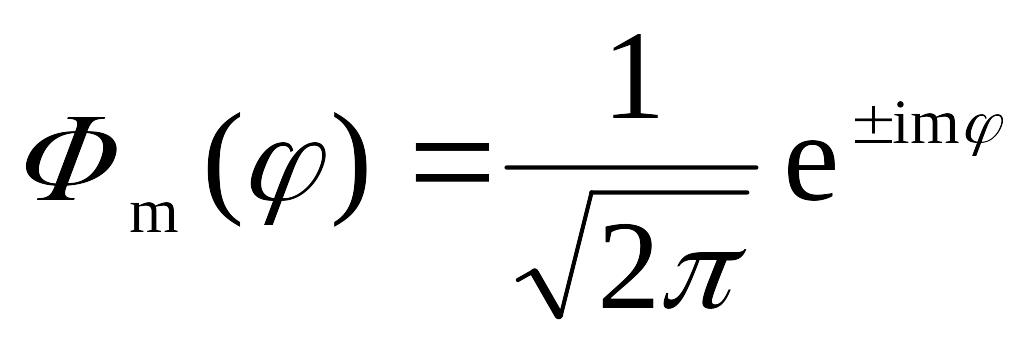(8)

Возможные значения параметра m найдем из условия однозначности функции ( ): или , т.е. .

К последнему выражению применим формулу Эйлера

= cos kx i sin kx, имеем cos2 m isin2 m = 1

Синус при всех углах 2 m должен быть равным нулю, а косинус - единице. А это возможно лишь при условии m = 0, (9)

Мы получили первое квантовое число m, которое может принимать только целочисленные значения, положительные и отрицательные, в том числе и нуль.

  Квантовое число n – главное. Оно определяет энергию электрона в атоме водорода и одноэлектронных системах (He+, Li2+ и т. д.). В этом случае энергия электрона

n принимает значения от 1 до ∞. Чем меньше n, тем больше энергия взаимодействия электрона с ядром. При n = 1 атом водорода находится в основном состоянии, при n > 1 – в возбужденном.

В многоэлектронных атомах электроны с одинаковыми значениями n образуют слой или уровень, обозначаемый буквами K, L, M, N, O, P и Q. Буква K соответствует первому уровню, L – второму и т. д.

Орбитальное квантовое число l характеризует форму орбиталей и принимает значения от 0 до n – 1. Кроме числовых l имеет буквенные обозначения

l	=	0	1	2	3	4	…
l	=	s	p	d	f	g	…

Электроны с одинаковым значением l образуют подуровень.

Квантовое число l определяет квантование орбитального момента количества движения электрона в сферически симметричном кулоновском поле ядра.

Квантовое число ml называют магнитным. Оно определяет пространственное расположение атомной орбитали и принимает целые значения от –l до +l через нуль, то есть 2l + 1 значений. Расположение орбитали характеризуется значением проекции вектора орбитального момента количества движения Mz на какую-либо ось координат (обычно ось z):

Все вышесказанное можно представить таблицей:

Орбитальное квантовое число Магнитное квантовое число Число орбиталей с данным значением l l ml 2l + 1 0 (s) 0 1 1 (p) –1, 0, +1 3 2 (d) –2, –1, 0, +1, +2 5 3 (f) –3, –2, –1, 0, +1, +2, +3 7

Таблица 1. Число орбиталей на энергетических подуровнях.

Орбитали одного подуровня (l = const) имеют одинаковую энергию. Такое состояние называют вырожденным по энергии. Так p-орбиталь – трехкратно, d – пятикратно, а f – семикратно вырождены.

s-Орбитали сферически симметричны для любого n и отличаются друг от друга только размером сферы. Их максимально симметричная форма обусловлена тем, что при l = 0 и μl = 0.

p-Орбитали существуют при n ≥ 2 и l = 1, поэтому возможны три варианта ориентации в пространстве: ml = –1, 0, +1. Все p-орбитали обладают узловой плоскостью, делящей орбиталь на две области, поэтому граничные поверхности имеют форму гантелей, ориентированных в пространстве под углом 90° друг относительно друга. Осями симметрии для них являются координатные оси, которые обозначаются px, py, pz.

d-Орбитали определяются квантовым числом l = 2 (n ≥ 3), при котором ml = –2, –1, 0, +1, +2, то есть характеризуются пятью вариантами ориентации в пространстве. d-Орбитали, ориентированные лопастями по осям координат, обозначаются dz² и dx²–y², а ориентированные лопастями по биссектрисам координатных углов – dxy, dyz, dxz.

Семь f-орбиталей, соответствующих l = 3 (n ≥ 4), изображаются в виде граничных поверхностей, приведенных на рис. 2.1.

Квантовые числа n, l и ml не полностью характеризуют состояние электрона в атоме. Экспериментально установленно, что электрон имеет еще одно свойство – спин. Упрощенно спин можно представить как вращение электрона вокруг собственной оси. Спиновое квантовое число ms имеет только два значения ms = ±1/2, представляющие собой две проекции углового момента электрона на выделенную ось. Электроны с разными ms обозначаются стрелками, направленными вверх и вниз .

В многоэлектронных атомах, как и в атоме водорода, состояние электрона определяется значениями тех же четырех квантовых чисел, однако в этом случае электрон находится не только в поле ядра, но и в поле других электронов. Поэтому энергия в многоэлектронных атомах определяется не только главным, но и орбитальным квантовым числом, а вернее их суммой: энергия атомных орбиталей возрастает по мере увеличения суммы n + l; при одинаковой сумме сначала заполняется уровень с меньшим n и большим l. Энергия атомных орбиталей возрастает согласно ряду

1s < 2s < 2p < 3s < 3p < 4s ≈ 3d < 4p < 5s ≈ 4d < 5p < 6s ≈ 4f ≈ 5d < 6p < 7s ≈ 5f ≈ 6d < 7p.

Итак, четыре квантовых числа описывают состояние электрона в атоме и характеризуют энергию электрона, его спин, форму электронного облака и его ориентацию в пространстве. При переходе атома из одного состояния в другое происходит перестройка электронного облака, то есть изменяются значения квантовых чисел, что сопровождается поглощением или испусканием атомом квантов энергии.