1. Уравнение Лагранжа примеры его составления. Функция Лагранжа, ее свойства.
Обобщенные координаты Аналитическое определение положения материальной точки, а следовательно и системы может быть осуществлено не только заданием декартовых прямоугольных координат, но и при помощи надлежащего количества параметров, через которые декартовы координаты выражаются однозначно. Рассмотрим этот вопрос подробнее.
У несвободной системы точек декартовы координаты удовлетворяют системе m независимых уравнений
( .1)
При помощи этих уравнений из 3n декартовых координат m могут быть выражены как однозначные функции остальных s = 3n - m декартовых координат. Будем условно именовать последние свободными координатами. Число свободных координат, таким образом, определяется числом степеней свободы материальной системы. Теперь выберем s независимых параметров q1, q2,...qs так, чтобы свободные декартовы координаты были однозначными функциями этих параметров:
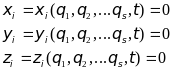( .2)
Т.к. несвободные координаты являются однозначными функциями свободных координат, то несвободные координаты являются однозначными функциями тех же параметров qk. Таким образом, все декартовы координаты могут быть выражены по формулам преобразования через s параметров qj и времени t. При этом уравнения связей ( .1) удовлетворяются тождественно. Определенные таким образом параметры qj называют обобщенными координатами несвободной механической системы. В качестве обобщенных координат могут выступать различные величины. Итак, обобщенными координатами механической системы называют независимые параметры q1, q2,...qs полностью определяющие конфигурацию этой системы, т.е. положение всех ее точек по отношению к системе отсчета.
Свойства
функции Лагранжа. Уравнения Лагранжа.
Определим функцию обобщенных координат,
скоростей и времени равенством
, где L называется
функций Лагранжа или лагранжианом
системы. Тогда уравнения Лагранжа
имеют вид
Свойства функции Лагранжа
Пусть механическая система состоит из двух частей А и В, каждая из которых будучи замкнутой, имела бы в качестве функции Лагранжа соответственно функции LA и LB . Тогда в пределе, при разведении частей настолько далеко, чтобы взаимодействием между ними можно было пренебречь, лагранжиан функции всей системы стремится к пределу:
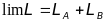Это свойство аддитивности функции
Лагранжа выражает собой тот факт, что
уравнения движения каждой из
невзаимодействующих частей не могут
содержать величины, относящиеся к
другим частям системы.
Очевидно, что умножение функции Лагранжа механической системы на произвольную постоянную само по себе не отражается на уравнениях движения. Отсюда, казалось бы, могла вытекать существенная неопределенность: функции Лагранжа различных изолированных механических систем могли бы умножаться на любые различные постоянные. Свойство аддитивности устраняет эту неопределенность - оно допускает лишь одновременное умножение лагранжевых функций всех систем на одинаковую постоянную, что сводится просто к естественному произволу в выборе единиц измерения этой физической величины
Прибавление полной производной по времени от произвольной функции обобщенных координат также не изменяет уравнений Лагранжа.
Таким образом, функция Лагранжа определена лишь с точностью до прибавления к ней полной производной от любой функции координат и времени.
Примеры составления уравнений Лагранжа – вопрос 4.