28. Перечислите свойства функции Лапласа φ(х).

1. Функция является четной, т.е.

φ(-х)= φ(х).

2. Функция φ(х) - монотонно убывающая при положительных значениях х, причем при х → ∞ φ(х) → 0.

(Практически можно считать, что уже при х > 4 φ(х)≈ 0.

3.

29 В чем заключаеся интегралная теорема Муавра – Лапласа. В каких случаях ее применяют.

Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события А в n независимых испытаниях заключено в пределах от а до b (включительно), при достаточно большом числе n приближенно равна

,

Где - функция (или интеграл вероятностей) Лапласа;

, .

Формула называется интегральной формулой Муавра­Лапласа. Чем больше n, тем точнее эта формула. При выполнении условия npq ≥ 20 интегральная формула , так же как и локальная, дает, как правило, удовлетворительную для практики погрешность вычисления вероятностей. Функция табулирована

30. Перечислите свойства функции Лапласа ф(х).

1)Нечётность Ф(-х)=-Ф(х);

2)Монотонно возрастающая Ф(х);

3)limФ(х)=1 {где х+}; limФ(x)=-1 {где х-}. На практике: если х5, полагаем что Ф(х)1 График у=Ф(х) в пределах от –1 до 1.

Следствие из интегральной теоремы Муавра Лапласа.

Пусть выполнили условие применимости интегральной теоремы М.Лапласа, тогда:

1)Вер-ть того, что число m наступлений события А в n испытаниях отличается от величины np не более, чем на эпсило (E) (по абсолютной величине) вычисл. По след. ф-ле:

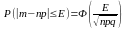
2)Вер-ть того что частость (доля) m/n наступлений событий А в n испытаниях отличается от вер-ти р не более чем на  (по абсолютной величине) вычисл. По след. ф-ле:

31. Сформулируйте теорему Пуассона. Как найти параметр λ?

Если вероятность р наступления события А в каждом испытании стремится к нулю (р → 0) при неограниченном увеличении числа n испытаний (n → 0), причем произведение nр стремится к постоянному числу λ(nр → λ), то вероятность Р_m,n того, что событие А появится m раз в n независимых испытаниях, удовлетворяет предельному равенству:

Т.е. условие теоремы Пуассона р → 0 при n → ∞, так что nр → λ, противоречит исходной предпосылке схемы испытаний Бернулли, согласно которой вероятность наступления события в каждом испытании р = const. Однако, если вероятность р - постоянна и мала, число испытаний n - велико и число λ = nр - незначительно (будем полагать, что λ = np ≤ 10), то из предельного равенства

вытекает приближенная формула Пуассона:

. Cобытия, для которых применима формула Пуассона, называют редкими так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).

   В качестве оценки неизвестного параметра λ по n наблюдённым значениям независимых случайных величин А₁,..., А_n используется их арифметическое среднее  А = (А₁ +... + А_n)/n, поскольку эта оценка лишена систсматической ошибки и её квадратичное отклонение минимально.  (λ — положительный параметр)

Случайные величины

32. Опрделение сучайной величиы. Примеры непрерывных и дискретных случайных величин.

Опр.: Случайной величиной называется переменная, кот. в рез-те испытания принимает то или иное числовое значение. Опр. Случайная величина назыв. дискретной, если число её возможных значений конечно или счётно (множество счетное, если его можно перенумеровать натур.альными .

числами). Опред.: Случ. величина назыв. непрерывной, если её значение полностью заполняют некоторый интервал. Пр1)число попаданий в мишень, (количество учеников в классе дискретная случ. величина; Пр2) рост человека, рост дереванепрерывная случ. величина.;