8.3.2 Одношаговые методы

Метод Эйлера (метод ломаной Эйлера) простейший явный численный метод. Он основан на разложении исходной функции в ряд Тейлора в окрестностях узлов x_i, i=0,1,…,k, в котором отбрасываются все члены, содержащие производные второго и более высоких порядков.

y(x_i+∆x_i)=y(x_i)+ y’(x_i) ∆x_i+…

y(x_i+h_i)=y(x_i)+ y’(x_i)h_i+…

y’(x_i)=f(x_i,y_i)

y(x_i+h_i)=y(x_i)+h_i f(x_i,y_i) i=1,2,…,k-1

Если для простоты h_i= h=const, то есть узлы x_i равноотстоящие, получаем

y_i+1= y_i+hf(x_i,y_i), i=1,2,…,k-1

y₀= y(х₀)

таким образом

y₁= y₀+hf(x₀,y₀)

y₂= y₁+hf(x₁,y₁)

…

Метод Эйлера имеет несколько модификаций

1. Усовершенствованный метод ломаных. Улучшенная ломаная (явный).

Сначала вычисляют промежуточные значения

а затем находят

2. Метод Эйлера с пересчетом. Усовершенствованный метод Эйлера (неявный).

Сначала вычисляют грубое значение

,

которое затем уточняют по формуле

или в виде одной формулы

3. Усовершенствованный метод Эйлера с уточнением. Усовершенствованный метод Эйлера с итерациями (неявный).

Сначала вычисляют

а затем это значение уточняют по формуле

Итерации продолжают до тех пор, пока в пределах требуемой точности два последовательных приближения не совпадут, то есть

Метод Рунге-Кутта

наиболее распространенный метод. Рассмотрим в нескольких вариантах

1-го порядка

y_i+1= y_i+hf(x_i,y_i)

2-го порядка

3-го порядка

4-го порядка

8.3.3 Многошаговые методы

могут быть получены следующим образом. Запишем исходное дифференциальное уравнение в виде

Проинтегрируем обе части этого уравнения по х на отрезке [x_i,x_i+1]. Интеграл от левой части легко вычисляется

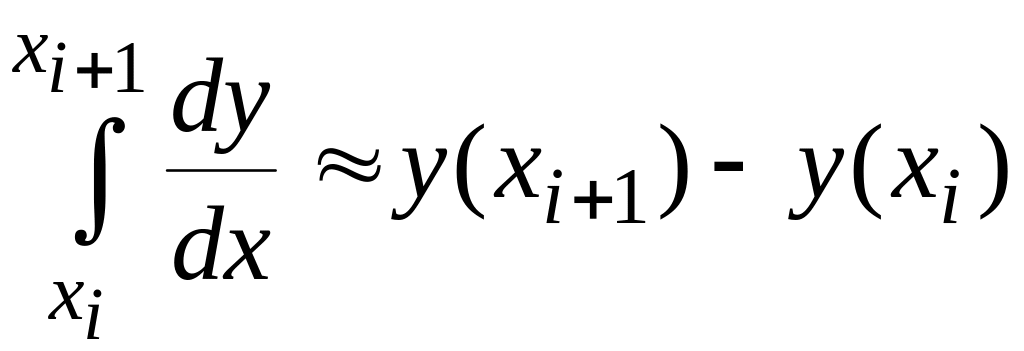
Для вычисления интеграла от правой части уравнения строится сначала интерполяционный многочлен степени r-1 P_r-1(x) для аппроксимации функции f(x,y) на отрезке [x_i,x_i+1] по значениям f(x_i-r+1,y_i-r+1), f(x_i-r+2,y_i-r+2),…,f(x_i,y_i). После этого можно написать

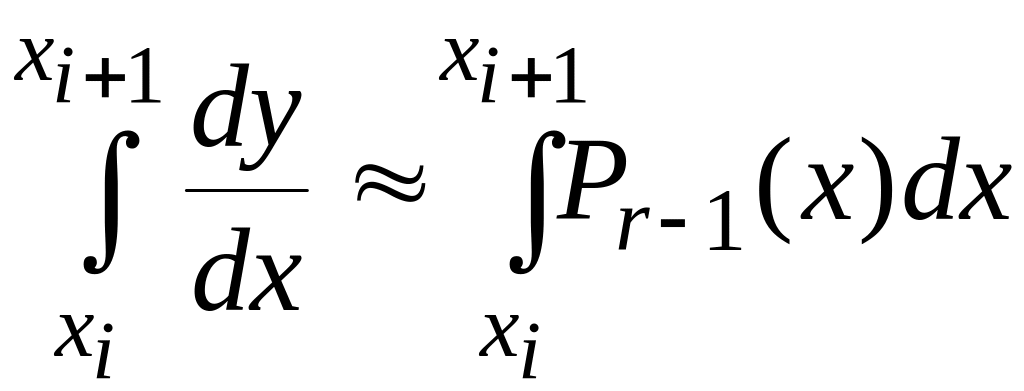
Таким образом, получаем

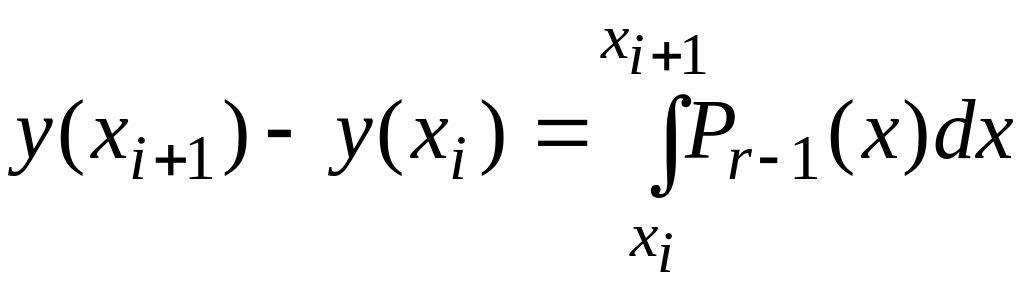
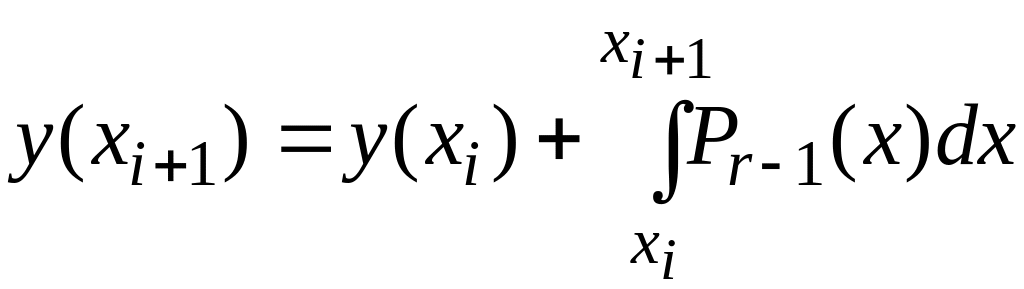
На основе этой формулы можно строить различные многошаговые методы любого порядка точности. Порядок точности зависит от степени интерполяционного многочлена , для построения которого используется значения сеточной функции y_i, y_i-1,…, y_i-r+1, вычисленные на r предыдущих шагах.

Широко распространенным семейством многошаговых методов являются методы Адамса (Адамса-Башфорта). Простейший из них, получающийся при

r=1 y_i+1= y_i+hf(x_i,y_i)

совпадает с рассмотренным ранее методом Эйлера первого порядка точности. В практических расчетах используют варианты

при r=2 (двухшаговый метод) .

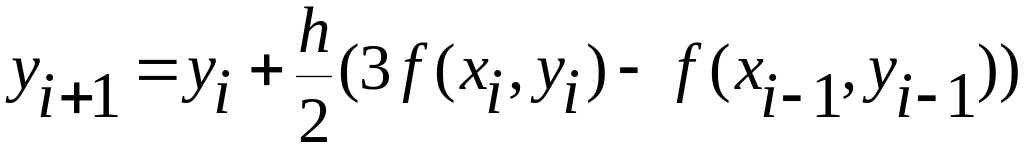При r=3 (трехшаговый метод)

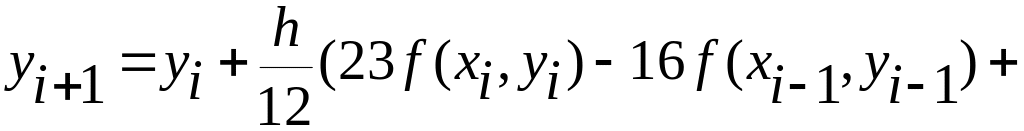
При r=4 (четырехшаговый метод)

,

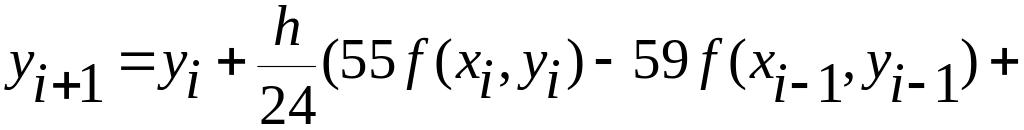
являющийся наиболее используемым.

При r=5 (пятишаговый метод)

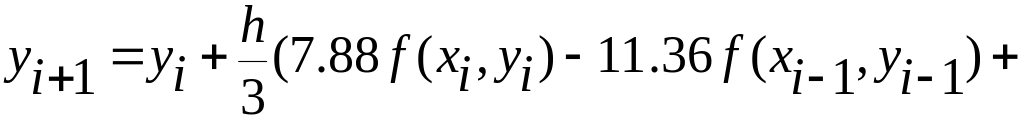
Для того, чтобы воспользоваться этими многошаговыми методами, необходимо предварительно каким-либо одношаговым методом найти решение на r-1 предыдущих шагах (в точках x₁, x₂,…,x_r-1).

Достоинство метода Адамса:

- экономичность, поскольку он требует вычисления лишь одного значения правой части на каждом шаге (метод Рунге-Кутта четвертого порядка – четырех)

Недостаток:

- невозможность начать счет только по начальным данным.

Рассмотренные методы Адамса относятся к явным многошаговым методам.

Среди многошаговых методов существуют и неявные схемы, так называемые методы прогноза и коррекции (они называются также методами предиктор-корректор). Суть этих методов состоит в следующем. На каждом шаге вводятся два этапа, использующих многошаговые методы:

1. С помощью явного метода (предиктора) по известным значениям функции в предыдущих узлах находится начальное приближение 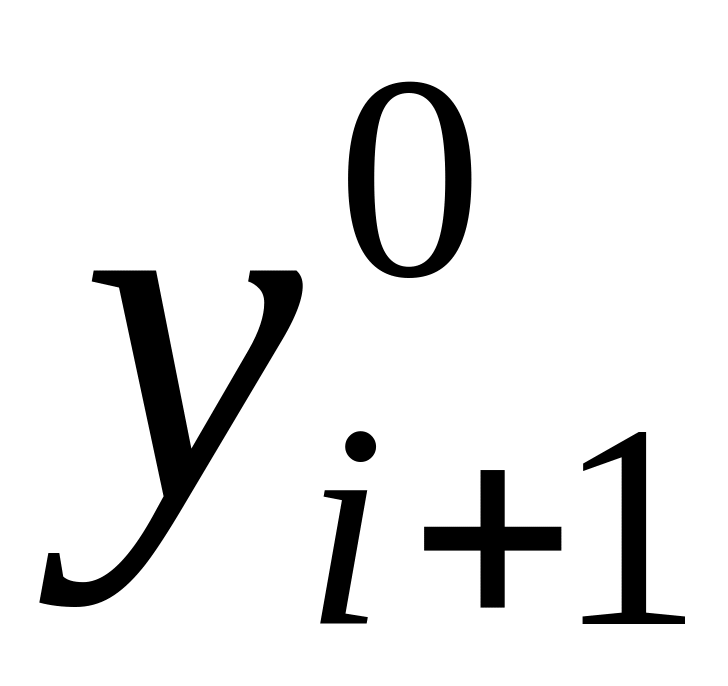, например, используя явный метод Адамса 4-го порядка

2. Используя неявный метод (корректор) в результате итераций находят приближения

до тех пор, пока не выполнится условие

Например, для этого может быть использован метод Адамса - Моултона при r=3

Явная схема используется на каждом шаге один раз, а с помощью неявной схемы реализуется итерационный процесс.

Заметим, что в этих формулах, как и в случае явного метода Адамса, необходимы значения сеточной функции в r-1 предыдущих точках.