Лекция №5 (2 семестр)

Тема: Теорема косинусов и Пифагора. Изоморфизм евклидовых пространств. Критерий изоморфности.

Содержание:

В силу неравенства Коши – Буняковского .

Пусть , – произвольные векторы пространства Е. Если считать их сторонами треугольника, то естественно считать третьей стороной треугольника вектор . Найдем длину :

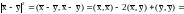
- теорема косинусов.

Если треугольник прямоугольный, то =0 и мы получаем теорему Пифагора: .

Изоморфизм евклидовых пространств.

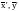Определение: Пусть Е и Е` – два евклидовых пространства. Они называются евклидово изоморфными, если они изоморфны как линейные пространства и для любых двух векторов из и их образов из Е`: .

Теорема: Для того, чтобы два евклидовых пространства были евклидово изоморфными, необходимо и достаточно, чтобы они имели одинаковую размерность.

Доказательство:

(необходимость) Пусть пространства Е и Е` – евклидово изоморфны, тогда в соответствии с определением евклидова изоморфизма они изоморфны как линейные пространства, а любые два линейных пространства над одним и тем же полем изоморфны тогда и только тогда, когда они имеют одинаковую размерность.

(достаточность) Пусть . Выберем (1) – ортонормированный базис Е, и пусть – ортонормированный базис Е`.

Возьмем произвольный вектор . Так как система (1) – базис пространства Е, то (3), а образ будем искать по формуле (4).

Легко видеть, что построенное нами правило является биективным отображением линейного пространства Е в линейное пространство Е`, более того, оно является изоморфизмом между Е и Е` как линейными пространствами.

Возьмем произвольные векторы и , а их образы вычислим по формуле (4): , .

Определение изоморфизма содержит требования равенства скалярных произведений ( , ) = (T( ), T( )), где Т – линейный изоморфизм. Однако это преобразование равносильно другому =| T( )|.

Покажем это. Если (x,y) = ( T(x),T(y)), то (x,x) = (T(x), T(x))  |x|² = | T(x)|² |x| = | T(x)|. Если |x| = | T(x)|, то |x-y| = | T(x-y)| => |x-y| = | T(x) – T(y)| => |x-y|² = | T(x) – T(y)|²= > (x-y)² = ( T(x) – T(y))² => |x|² – 2(x,y) + |y|² = | T(x)|² – 2( T(x) – T(y))² + | T(y)|² => -2(x,y) = -2( T( x), T(y)) т.к. по предположению |x| = | T(x)| => (x,y) = ( T(x), T(y)).

Библиография:

1. Воеводин В.В. Линейная алгебра. СПБ.: Лань, 2008, 416 с.

2. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2006, 304 с.

3. Кострикин А.И. Введение в алгебру. часть II. Основы алгебры: учебник для вузов, -М. : Физико-математическая литература, 2000, 368 с.

Лекция №6 (2 семестр)

Тема: Наклонная, перпендикуляр и проекция в евклидовом пространстве. Унитарное пространство.

Содержание:

Наклонная, перпендикуляр и проекция в евклидовом пространстве.

Рассмотрим сначала эти понятия в пространстве радиус–векторов, закрепленных в точке О (V₃). Пусть дана плоскость L. Выберем на плоскости точку О и рассмотрим множество всех радиус–векторов, закрепленных в этой точке.

Из некоторой точки М опустим на эту плоскость перпендикуляр. М_L– основание этого перпендикуляра. Построение перпендикуляра, опущенного из точки М на плоскость L сводится к разложению вектора в сумму:

(1), где .

Так как из точки М можно провести только один перпендикуляр, на плоскость L, то такое разложение существует и единственно.

Пусть теперь Е – произвольное евклидово пространство, и пусть L – некоторое его подпространство. Возьмем произвольный вектор и представим его в виде суммы: (2), где .

Определение: Вектор в разложении (2) называется проекцией вектора на подпространство L, вектор называется перпендикуляром, опущенным из на L, а сам вектор называется наклонной к подпространству L.

Заметим также, что условие эквивалентно условию , а так как евклидово пространство Е представимо в виде , то разложение (2) существует и единственно. Векторы и в разложении (2) ортогональны, и тогда по теореме Пифагора , откуда вытекает, что , т.е. длина наклонной не меньше длины перпендикуляра. тогда и только тогда, когда . Рассмотрим введенное понятия наклонной, перпендикуляра и проекции с алгебраической точки зрения: при фиксированном подпространстве L любой вектор евклидова пространства Е однозначно определяет по отношению к этому подпространству две своих компоненты, а именно: компоненту , которая называется проекцией и компоненту , называемую перпендикуляром, следовательно, можно считать, что разложение (2) определяет две функции и 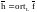. Аргументами этих функций служат все векторы из Е, значением функции является вектор из L, а значением функции является вектор, принадлежащий .

Так как , то проекция вектора , а 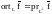. Возьмем произвольные векторы и , принадлежащие Е.

Откуда следует, что

(7)

Аналогично выводятся соответствующие выражения для функции ort:

(8)

Заметим, что для любого вектора , принадлежащего L, . Из первого равенства системы (8) следует, что , следовательно, значение функции орт не меняется, если к аргументу прибавить любой вектор из подпространства L, в частности, если взять в качестве – , то получим , аналогично .

Пусть теперь подпространство L является ортогональной суммой L₁ и L₂. Произвольный вектор евклидова пространства Е можно представить в виде: , где , а .

Таким образом, .

Перпендикуляр, опущенный из вектора на подпространство , равен одному из выражений .

Если , то .

Унитарные пространства.

Определение: Комплексное линейное пространство U называется унитарным, если любой паре векторов из U поставлено в соответствие комплексное число , называемое скалярным произведением, причем выполнены следующие аксиомы:

1)

2)

3)

4)

Примером унитарного пространства может служить С_n (арифметическое пространство n-мерных векторов), если для векторов и 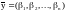скалярное произведение выполняется по формуле:

В унитарном пространстве U, так же, как и в вещественном, вводится понятие длины: .

У любого ненулевого вектора длина больше 0, а длина нулевого вектора равна 0.

Для произвольного комплексного числа и любого вектора, принадлежащего U . Также, как и в R_n, в С_n выполняется неравенство Коши–Буняковского: .

Библиография:

1. Воеводин В.В. Линейная алгебра. СПБ.: Лань, 2008, 416 с.

2. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2006, 304 с.

3. Кострикин А.И. Введение в алгебру. часть II. Основы алгебры: учебник для вузов, -М. : Физико-математическая литература, 2000, 368 с.