Лекция №22 (II семестр)

Тема:Теорема о существовании и единственности разложения оператора в прямую сумму операторов с заданными характеристическими многочленами. Корневые подпространства. Теорема Гамильтона-Кэли.

Содержание:

Теорема : С помощью любого операторного многочлена можно осуществить разложение оператора А в прямую сумму.

Доказательство: Рассмотрим последовательность операторов

Этим операторам соответствуют ядра .

1. Покажем сначала, что если существует , такое, что

.

Доказательство:

Пусть

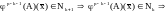
2. Рассмотрим для операторов их образы , т.е. – область значений оператора , мы знаем, что .

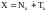Пусть q – наименьшее целое положительное число, такое, что , ему соответствует образ , . В самом деле, если вектор

Каждый из корней характеристического многочлена оператора, индуцированного оператором А на подпространство является корнем многочлена . Ни один из корней характеристического многочлена оператора, индуцированного оператором А на подпространство , не является корнем многочлена , в самом деле, нам известно, что все собственные векторы оператора А должны находиться в подпространствах и , при этом в находятся те из них, которые соответствуют собственным значениям, совпадающим с какими-то корнями многочлена , а в находятся те из них, для которых собственные значения не совпадают ни с какими корнями многочлена .

Теорема : Пусть характеристический многочлен оператора представим в виде произведения двух многочленов: , не имеющих общих корней. Тогда оператор А можно единственным образом разложить в прямую сумму операторов В и С ( ), так, что оператор В имеет характеристический многочлен , а оператор С – .

Доказательство:

1. Рассмотрим разложение оператора А в прямую сумму, получающуюся с помощью многочлена . Так как произведение характеристических многочленов операторов, определяющее прямую сумму, совпадает с многочленом , то существование такого разложения вытекает из теоремы 16.

2. Пусть , где подпространства N и T инвариантны относительно оператора А и при этом оператор, индуцированный оператором А на подпространство N, имеет в качестве характеристического многочлена , а оператор, индуцированный оператором А на подпространство Т, имеет в качестве характеристического многочлена . Тогда, по теореме 13, для всех достаточно больших k, но отсюда следует, что . Оператор является невырожденным на Т, так как – характеристический многочлен оператора, индуцированного оператором А на T, и и не имеют общих корней, следовательно, множество образов векторов из T по отношению к оператору совпадает с T, но тогда для . Подпространства N и T и и в прямой сумме образуют все пространство X. Мы имеем, что , , и .

Пусть оператор , . Пусть – характеристический многочлен оператора А. Так как все происходит на комплексном линейном пространстве С, то , где – собственные значения (попарно различные), . Рассмотрим многочлены . Они являются делителями характеристического многочлена , и никакая пара из них не имеет общих корней. По теореме 17 существуют инвариантные подпространства относительно оператора А такие, что , при этом размерности , . Характеристический многочлен оператора, индуцированного оператором А на подпространство – это .

Определение: Подпространства называются корневыми подпространствами оператора А, соответствующими собственному значению . Векторы корневого подпространства называются корневыми векторами.

Т.о., оператор А может быть разложен в прямую сумму операторов, индуцированных этим оператором на корневых подпространствах. Корневое подпространство совпадает с ядром оператора при некотором целом положительном q. В действительности, в данном случае можно считать . В самом деле, рассмотрим операторы , где . Пусть – это наименьшее число, для которого ядро оператора совпадает с ядром оператора . Тогда корневое подпространство будет совпадать с ядром оператора , т.к. размерность ядер операторов 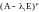при монотонно возрастает, а размерность корневого подпространства , то , т.е. .

Т.о., корневое подпространство , соответствующее собственному значению кратности совпадает с ядром оператора .

Теорема : (Теорема Гамильтона-Кэли)

Если – характеристический многочлен оператора А, то – нулевой оператор (оператор является корнем своего характеристического многочлена).

Доказательство: Пусть . Так как линейное пространство X представимо в виде прямой суммы корневых подпространств , то вектор единственным образом представим в виде: , где .

так как .

Библиография:

1. Воеводин В.В. Линейная алгебра. СПБ.: Лань, 2008, 416 с.

2. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2006, 304 с.

3. Кострикин А.И. Введение в алгебру. часть II. Основы алгебры: учебник для вузов, -М. : Физико-математическая литература, 2000, 368 с.