Лекция №21 (II семестр)
Тема: Прямая сумма оператора и её свойства. Теорема о разложении оператора в прямую сумму с помощью операторного многочлена.
Содержание:
Теорема
:
Пусть
линейный оператор
,
L
– произвольное
подпространство
линейного
пространства
X,
инвариантное
относительно оператора
А. Если
все собственные значения оператора,
индуцированного оператором
А на
подпространство
L
являются
корнями многочлена
,
то
подпространство
L
содержится
в ядре операторного многочлена
для
всех достаточно
больших
k.
Доказательство:
1.
Пусть
– область значений оператора,
индуцированного на подпространство L
операторным многочленом
,
т.е.
.
Оператор
вырожден на подпространстве L,
т.к. если
– собственный вектор оператора А,
принадлежащий L,
т.е.
,
то, по условию,
,
а тогда, по лемме 3
.
Т.о., существуют ненулевые векторы
,
принадлежащие ядру оператора
,
а тогда
содержится в L,
потому что
инвариантно относительно оператора А
(по лемме 1), и
.
2.
является подпространством линейного
пространства L,
если это подпространство нулевое, то
доказывать нечего, т.к. в этом случае
,
а тогда
,
k=1.
Пусть
– ненулевое. Согласно лемме 1,
(равное
)
является инвариантным относительно
оператора
.
По следствию из основной теоремы алгебры,
оператор А, действующий из
в
имеет, по крайней мере, одно собственное
значение
,
а так как характеристический многочлен
индуцированного оператора
,
является делителем характеристического
многочлена порождающего оператора
,
то
,
будучи собственным значением последнего,
является корнем многочлена
,
т.е.
,
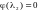а тогда индуцированный оператор
,
действующий из
в
,
вырожден (по лемме 3) и тогда
и
.
Имеем последовательность:
,
где
,
Продолжая рассуждение в том же духе, получим последовательность:
.
Так как
не может бесконечно уменьшатся с ростом
k,
то существует k
такое, что
– нулевое подпространство, а тогда
,
а тогда это и означает, что
.
Теорема 14: Любой линейный оператор А, действующий в m-мерном комплексном пространстве X, имеет по крайней мере одно инвариантное подпространство размерности m-1.
Доказательство:
Т.к. линейное пространство X
рассматривается над полем комплексных
чисел, то по основной теореме алгебры
этот линейный оператор имеет по крайней
мере один собственный вектор
.
Пусть этот вектор соответствует
собственному значению ,
т.е.
.
Рассмотрим операторный многочлен
,
соответствующий многочлену
.
По лемме 1, область значений операторного
многочлена
,
которую мы обозначили
,
является подпространством, инвариантным
относительно оператора А. По лемме 3
оператор
вырожден, следовательно
.
Пусть
L
– произвольное подпространство линейного
пространства X,
имеющее размерность
и содержащее
в себе в качестве подпространства.
Покажем,
что пространство L
– искомое, т.е., что оно инвариантно
относительно А. Рассмотрим произвольный
вектор
.
(
,
но с другой стороны,
,
где
L
– инвариантно относительно А.
Приведение матрицы оператора к треугольному виду.
Пусть
.
Теорема
15:
Для
произвольного линейного оператора
А, действующего
в
m-мерном
линейном пространстве
X,
существуют
инвариантные относительно
этого
оператора подпространства
,
размерности
соответственно,
такие, что
.
Доказательство:
Существование
и
очевидно:
.
По теореме 14, в
существует инвариантное относительно
оператора А подпространство
.
Рассмотрим оператор
,
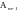индуцированный оператором А на
подпространство
,
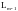и к этому оператору опять применим
теорему 14, в соответствии с которой этот
оператор обладает инвариантным
подпространством размерности
.
Аналогично доказывается существование
...
.
Теорема доказана.
Матричная интерпретация теоремы 15.
Построим
базис линейного пространства X
следующим образом:
– произвольный ненулевой вектор
подпространства L
(
),
– любой вектор из
,
,
...
Построим матрицу оператора в этом базисе:
Матрица
называется правой
треугольной матрицей.
Следствие: Любая квадратная матрица подобна правой треугольной матрице.
Доказательство:
Пусть
– произвольная квадрантная матрица
вида
.
Если в пространстве X
зафиксирован базис
,
то матрица
является матрицей некоторого линейного
оператора А, действующего из X
в X.
По доказанному выше, в линейном
пространстве X
существует базис
,
для которого матрицей оператора А
является правая треугольная матрица
.
и
– матрицы одного и того же оператора в
разных базисах, которые, как известно,
подобны.
Лемма: Если оператор А в некотором базисе имеет треугольную матрицу , то диагональные элементы матрицы совпадают с собственными значениями оператора А с учетом их кратности.
Доказательство:
Прямая сумма операторов.
Пусть
.
Пусть линейные операторы
,
а
.
Тогда
существует единственное разложение:
.
Отображение
А, определяемое равенством
называется прямой
суммой операторов
В и С. Если одно из подпространств L
или М – тривиально, то и прямая сумма в
этом случае называется тривиальной.
Свойства прямой суммы операторов.
1. Отображение А, является линейным оператором.
Доказательство:
Пусть
,
и пусть ,
– любые числа.
Тогда:
2. Единственность представления оператора в виде прямой суммы.
,
то есть,
– индуцированный оператор А на L.
,
то есть,
– индуцированный оператор А на М.
3. Пусть А – произвольный оператор, действующий в линейном пространстве X. Если и подпространства L и М – инвариантны относительно оператора А, то оператор А всегда разложим в прямую сумму.
В
этом случае характеристический многочлен
оператора А равен произведению
характеристических многочленов
операторов
и
,
индуцированных оператором А на
подпространства L
и М соответственно.
Библиография:
1. Воеводин В.В. Линейная алгебра. СПБ.: Лань, 2008, 416 с.
2. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2006, 304 с.
3. Кострикин А.И. Введение в алгебру. часть II. Основы алгебры: учебник для вузов, -М. : Физико-математическая литература, 2000, 368 с.