Лекция №1 (2 семестр)

Тема: Определение евклидова пространства. Примеры. Неравенство Коши-Буняковского. Ортогональные системы и их линейная независимость.

Содержание:

Определение евклидовых пространств.

При изучении линейных пространств мы обобщили понятие плоскости, трехмерного пространства следующим образом: мы определили линейное пространство X над произвольным полем Р как непустое множество, замкнутое относительно операции сложения, для элементов которого определена операция умножения на элементы из поля Р, так что выполнены следующие 8 аксиом линейного пространства:

– ассоциативность.

– существование нейтрального элемента.

– существование симметричного элемента.

– коммутативность. (Х – абелева группа по сложению)

.

.

.

.

Понятие n-мерного линейного пространства далеко не в полной мере обобщает понятие плоскости и понятие трехмерного пространства. В линейном n‑мерном пространстве L не определены такие понятия, как длина вектора и угол между векторами. Как известно, и в плоскости, и в трехмерном пространстве можно ввести понятие скалярного произведения векторов – это понятие вводится с помощью понятий длины вектора и угла между векторами: . Мы установили, что скалярное произведение обладает следующими свойствами:

1)

2)

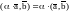
3)

4)

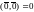
Если известно скалярное произведение, то легко можно вычислить длину вектора (1). По известному скалярному произведению можно определить и угол между векторами: (2). Это наталкивает на следующий способ обобщения плоскости и пространства: мы аксиоматически определяем в любом n-мерном линейном пространстве понятие скалярного произведения так, чтобы выполнялись свойства 1,2,3,4. Тогда понятия длины вектора и угла между векторами определим по формулам (1) и (2), однако за достигнутое таким образом углубление в геометрию пространства нам придется пожертвовать некоторой степенью общности: мы будем рассматривать линейные пространства, заданные не над произвольным полем Р, а лишь над полями R и С.

Определение: Вещественное пространство Е, заданное над полем R, называется евклидовым, если любой паре и элементов пространства Е поставлено в соответствие число, обозначаемое и называемое скалярным произведением, так, что выполнены следующие аксиомы:

1)

2)

3)

4)

Отметим, что из аксиомы (2) при следует, что , а из аксиом (2) и (3) следует, что скалярное произведение двух линейных комбинаций вычисляется по формуле: (3).

Очевидно, что любое подпространство евклидова пространства Е само является евклидовым пространством, введенным над тем же полем. Если L_n – n-мерное линейное пространство над R, то оно может быть легко превращено в евклидово пространство, например, следующим образом: в пространстве L_n выберем базис , тогда произвольный векторы и могут быть записаны в виде линейных комбинаций:

, а тогда скалярное произведение: (4).

Легко проверить, что для произведения, определяемого по формуле (4), выполнены аксиомы 1,2,3,4. То есть, формула (4) в действительности задает скалярное произведение. Заметим, что скалярное произведение в n-мерном пространстве можно задать и другим способом: например, взять произвольную последовательность положительных действительных чисел и положить .

В n-мерном пространстве базис, как известно, можно выбрать многими способами, а любому базису по указанному выше правилу соответствует свое скалярное произведение.

Определение: Вектор из евклидова пространства Е называется нормированным, если . Справедливо следующее утверждение: любой ненулевой вектор можно нормировать, умножив его на некоторое действительное число .

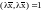
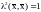
Определение: Система векторов евклидова пространства Е называется нормированной, если нормированы все ее элементы.

Теорема: ( неравенство Коши – Буняковского )

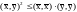Для любых векторов евклидова пространства Е справедливо неравенство: (5).

Доказательство: Неравенство (5) очевидно, справедливо, если один из векторов равен 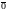, например, . (В этом случае оно превращается в равенство, поэтому будем считать .)

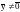Рассмотрим вектор 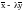, где – произвольное число из R.

Положим (6).

Определение: Пусть и – произвольные векторы из Е. Векторы называются коллинеарными, тогда и только тогда, когда:

.

Так как – нулевой вектор, то два вектора заведомо коллинеарны, если хотя бы один из них – нулевой.

Теорема: Неравенство Коши – Буняковского обращается в равенство тогда и только тогда, когда векторы и коллинеарны.

Доказательство:

1) Пусть векторы и коллинеарны, :

2) Пусть . Если вектор , то векторы и коллинеарны, и доказывать нечего.

Предположим, что . Возьмем , тогда:

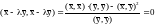, так как неравенство в этом случае является равенством, а тогда .

Ортогональность.

Определение: Векторы , принадлежащие евклидову пространству Е называются ортогональными, если их скалярное произведение равно 0. Определение ортогональности является перенесением понятия перпендикулярности на произвольные евклидовы пространства.

Определение: Система векторов евклидова пространства Е называется ортогональной, если она состоит из одного вектора или все векторы этой системы попарно ортогональны.

Определение: Нормированная ортогональная система векторов называется ортонормированной.

Пример:

В пространстве V₃ векторы образуют ортонормированную систему.

В арифметическом пространстве трехмерных векторов ортонормированной является система:

Теорема: Любая ортогональная система ненулевых векторов евклидова пространства Е линейно независима.

Доказательство: Пусть дана система ортогональная векторов :

Рассмотрим произвольную нулевую линейную комбинацию:

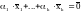
(1)

Умножая обе части неравенства (1) поочередно на , покажем, что все

Следствие: Если сумма попарно ортогональных векторов равна , то все векторы равны .

Библиография:

1. Воеводин В.В. Линейная алгебра. СПБ.: Лань, 2008, 416 с.

2. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2006, 304 с.

3. Кострикин А.И. Введение в алгебру. часть II. Основы алгебры: учебник для вузов, -М. : Физико-математическая литература, 2000, 368 с.