
- •Введение
- •Тема 1. Логика высказываний
- •1.1. Понятие высказывания
- •1.2. Логические операции
- •1. Отрицание или инверсия ( – не)
- •Конъюнкция ( ,, ·, логическое и )
- •4. Импликация ( ) “если а, то b”
- •6. Сумма по модулю два
- •7. Штрих Шеффера ( , обратная конъюнкция и – не)
- •8. Стрелка Пирса ( , обратная дизъюнкция или – не )
- •1.3. Булевы функции
- •1.3.1. Некоторые определения из теории множеств
- •1.3.2. Булевы функции
- •1.4. Формулы
- •1.5. Равносильные формулы
- •1.6. Подстановка и замена
- •1.7. Формы представления высказываний
- •1.8. Минимизация сложных высказываний методом Квайна
- •1.9. Полные системы функций
- •1.9.1. Система функций { }
- •1.9.2. Замкнутые классы
- •1.9.3. Функциональная полнота
- •Тема 2. Логические исчисления
- •2.1. Интерпретация формул
- •2.2. Примеры тождественно истинных формул высказываний
- •2.3. Формальные теории
- •Выводимость.
- •2.5. Интерпретация формальных теорий
- •2.6. Исчисление высказываний.
- •2.7. Производные правила вывода
- •2.8. Дедукция
- •2.9. Некоторые теоремы теории £
- •Тема 3. Логика и исчисление предикатов
- •3.1. Предикаты
- •3.2. Исчисление предикатов
- •3.3. Интерпретация
- •3.4. Основные равносильности для предикатов
- •3.5. Приведенная форма представления предикатов
- •Тема 4. Автоматическое доказательство теорем
- •4.1. Постановка задачи
- •4.2. Доказательство от противного
- •4.3.Правило резолюции для исчисления высказываний
- •4.4. Правило резолюции для исчисления предикатов
- •4.5. Основные положения мр (выводы)
- •4.6. Логическое программирование
- •Тема 5. Теория алгоритмов
- •5.1. Интуитивное понятие алгоритма
- •5.2. Конкретизация понятия алгоритма
- •5.2.1. Машины Тьюринга
- •5.2.3. Рекурсивные функции
- •5.2.3. Нормальные алгорифмы Маркова
- •5.3. Алгоритмически неразрешимые проблемы
- •5.3.1. Проблема самоприменимости
- •5.3.1.1. Нумерация мт
- •5.3.1.2. Самоприменимость мт
- •5.3.2. Проблема останова
- •5.3.3. Разрешимые и неразрешимые задачи математики
- •5.4. Характеристики сложности вычислений
- •5.5. Классы сложности задач
- •5.5.1. Р задачи
- •5.5.2. Np задачи
1.9.3. Функциональная полнота
Класс функций F называется полным, если его замыкание совпадает с Pn:
![]() .
.
Другими словами, множество функций F образует полную систему, если любая функция реализуема в виде формулы над F.
Теорема.
Пусть заданы две системы функций
![]() и
и
![]() .
.
Тогда, если система F – полная и все функции из F реализуемы формулами над G, то система G тоже полная.
Доказательство. Пусть h
– произвольная функция,
![]() .
Тогда [F]=Pn,
следовательно, h реализуема
формулой
,
базисом которой является F
(
.
Тогда [F]=Pn,
следовательно, h реализуема
формулой
,
базисом которой является F
(![]() ).
Если выполнить замену подформулы fi
на подформулу
).
Если выполнить замену подформулы fi
на подформулу
![]() в формуле
,
то мы получим формулу над G.
в формуле
,
то мы получим формулу над G.
Следовательно, функция h
реализуется формулой
![]() .
.
Примеры:
Система {
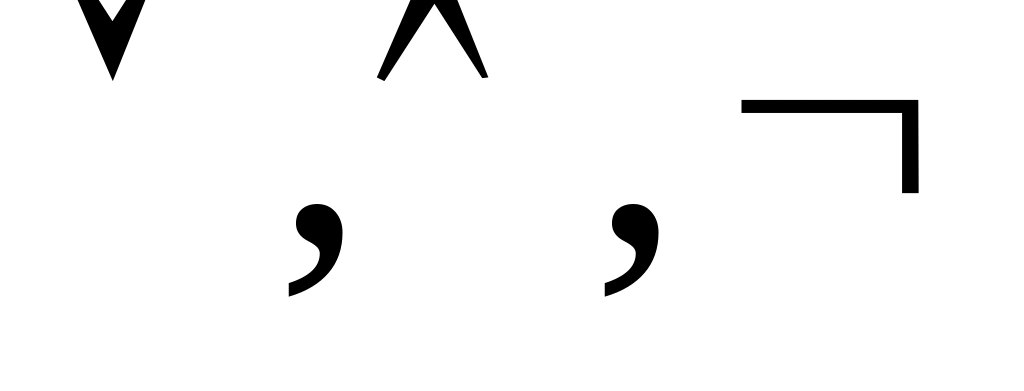 }
– полная, т. к. любая логическая операция
может быть выражена через дизъюнкцию,
конъюнкцию и отрицание;
}
– полная, т. к. любая логическая операция
может быть выражена через дизъюнкцию,
конъюнкцию и отрицание;Система {
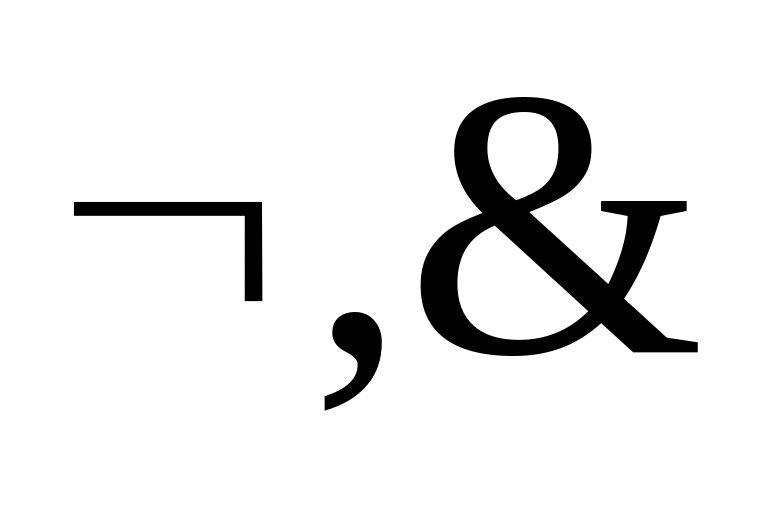 }
– полная, т. к.
}
– полная, т. к.
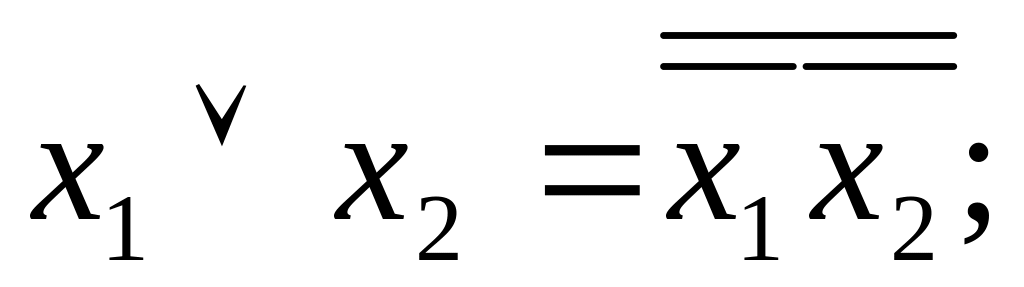
Система {
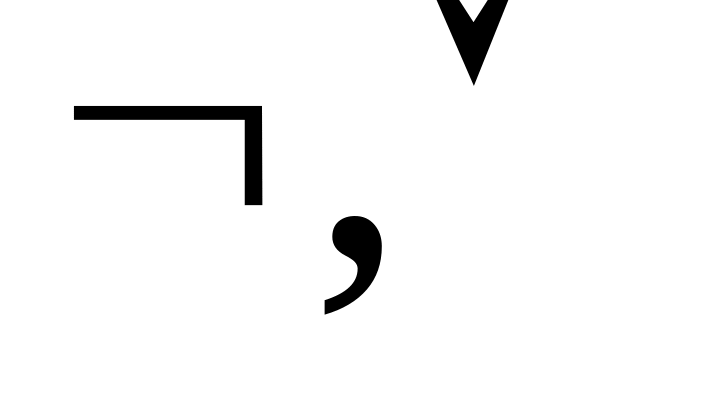 }
– полная, т. к.
}
– полная, т. к.
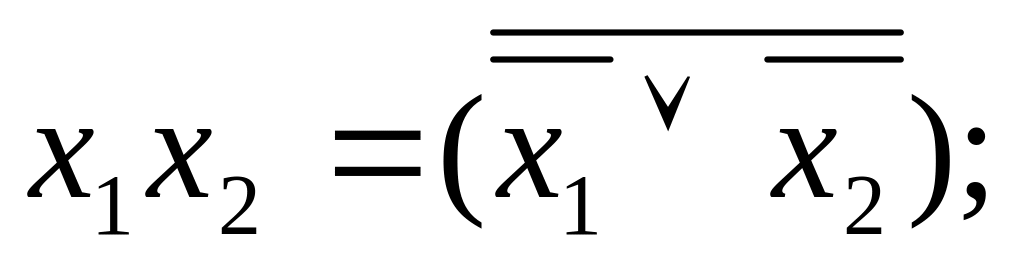
Система {|} – полная, т. к.
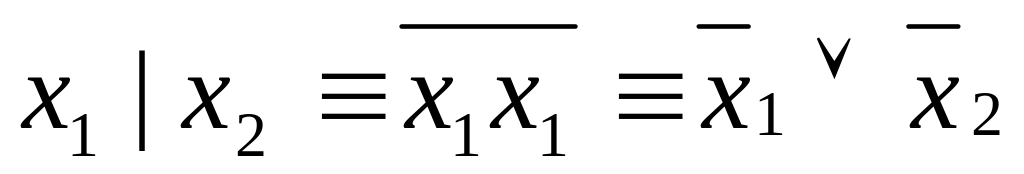 ,
а {
}и{
}
– полные системы.
,
а {
}и{
}
– полные системы.Система {
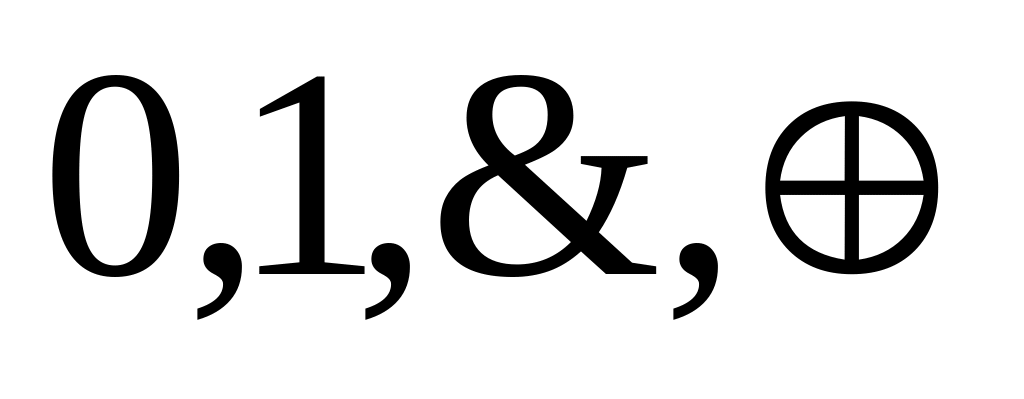 }
– полная, т. к.
}
– полная, т. к.
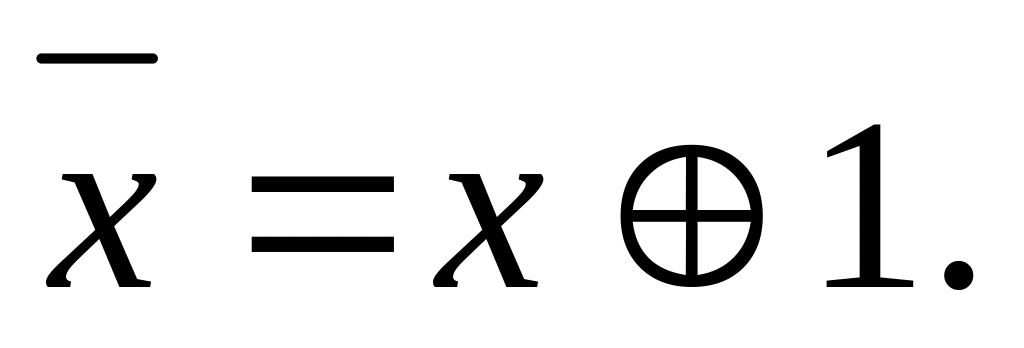 Представление
логической операции системой{
}называется
полиномом Жегалкина. Таким образом,
всякая логическая операция представима
в виде
Представление
логической операции системой{
}называется
полиномом Жегалкина. Таким образом,
всякая логическая операция представима
в виде
![]() где
где
![]() - сложение по модулю 2, знак · обозначает
конъюнкцию,
- сложение по модулю 2, знак · обозначает
конъюнкцию,
![]() .
.
Теорема Поста: Система логических операций полна тогда и только тогда, когда она содержит хотя бы одну функцию, не сохраняющую 0, одну функцию, не сохраняющую 1, хотя бы одну несамодвойственную функцию, хотя бы одну нелинейную функцию и хотя бы одну немонотонную функцию.
Пример.
Докажем полноту системы {,,1}.
f |
T0 |
T1 |
T* |
TL |
TM |
В каждом столбце должен быть хотя бы один «-» |
xy |
+ |
- |
- |
+ |
- |
|
xy |
+ |
+ |
- |
- |
+ |
|
1 |
- |
+ |
- |
+ |
+ |
Проверка на принадлежность классу T0.
![]()
![]()
![]()
Проверка на принадлежность классу T1.
![]()
![]()
![]()
Проверка на принадлежность классу T*.
![]()
![]()
![]()
Проверка на принадлежность классу TL.
![]()
![]()
![]()
Проверка на принадлежность классу TM.
![]()
f(0,0)=0
f(0,1)=1
f(1,0)=1
f(1,1)=0
![]()
f(0,0)=0
f(0,1)=1
f(1,0)=1
f(1,1)=1
![]()
Тема 2. Логические исчисления
Основная задача математической логики – формализация правильных способов рассуждения. Элементами логических рассуждений являются утверждения, которые либо истинны, либо ложны (простые высказывание или пропозициональные переменные). Из простых высказываний с помощью логических связок (операций) могут быть построены сложные высказывания.
Таблицы истинности позволяют ответить на многие вопросы, касающиеся формул логики высказываний: о равносильности формул, о противоречивости и т. п. Но более сложные вопросы решить с помощью таблиц истинности нельзя. Поэтому рассмотрим другой метод – метод формальных аксиоматических теорий.
2.1. Интерпретация формул
Пусть A(x1,x2,…xn) – пропозициональная формула, где x1,x2,…xn – пропозициональные переменные. Конкретный набор значений, который принимают переменные x1,x2,…xn называется интерпретацией.
I(A) – значение формулы в интерпретации I.
В одной интерпретации формула может быть истинной, а в другой – ложной.
Формула, истинная в какой- то интерпретации – выполнимая.
Формула истинная во всех интерпретациях – тавтология (тождественно истинная формула), иначе – противоречие.
Пример 1.
Докажем, что формула является тавтологией.
![]()
Пример 2.
Докажем, что формула является выполнимой.
![]()
