Point 4. Nonhomogeneous equations Structure of the general solution of so lnde

Theorem 6 (structure of the general solution of the second order linear nonhomogeneous differential equation (1)). The general solution of SO LNDE equals the sum of the general solution of corresponding [associated] LHDE (3) and some particular solution of the given equation,

. ( 18 )

■ Let is the general solution of LHDE (3), where are two linearly independent solutions of LHDE. A function

is a solution of the equation (1) for any values of because of

.

We have only to prove that for any initial conditions (2) one can find values of to satisfy these conditions. Since

,

we get a system of linear equations in

which has unique solution because of its principal determinant is and doesn’t equal zero on account of linear independence of .■

Ex. 11. A function is the general solution of a differential equation .

Indeed, is the general solution of the corresponding homogeneous equation (see Ex. 6, 9), and a function is a particular solution of the given equation.

Method of variation of arbitrary constants

Let we must find the general solution of SO LNDE (1). We can do it with Lagrange in the next two steps.

1. We find the general solution

of the corresponding LHDE (3), where are its linearly independent solutions.

2. Now we find the general solution of SO LNDE (1) in the same form as , but we treat as unknown functions, namely

. ( 19 )

We find the first derivative of y,

,

and we suppose that

.

Then

.

Substituting the values of in the equation (1), we have

.

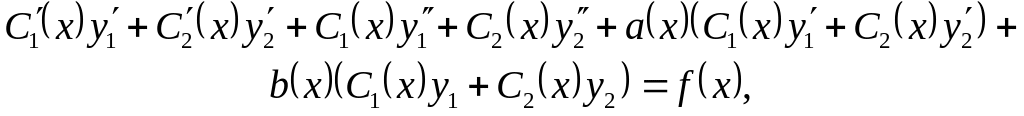
We get the next system of linear equations in

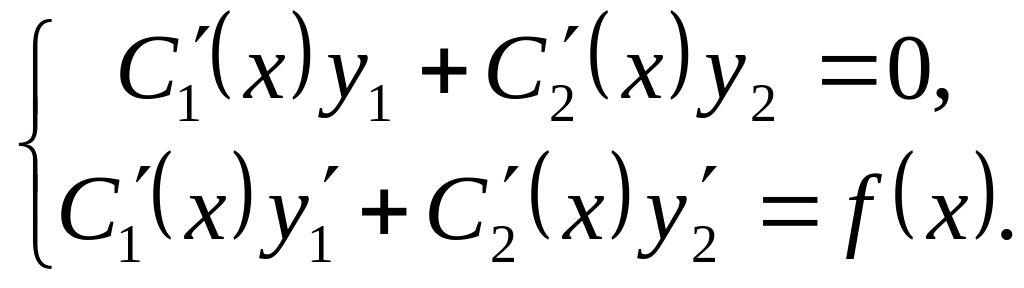( 20 )

Solving the system (20) we get

,

where be some functions. Integrating, we have finally

( 21 )

where are arbitrary constants. The general solution of the equation (1) is

. ( 22 )

Note 1. We can represent the general solution (22) in the next form:

,

and we see that

is the general solution of the homogeneous equation (3) and

is the particular solution of the nonhomogeneous equation (1).

Ex. 12. Find the general solution of an equation .

1. Corresponding LHDE is , its characteristic equation

has real equal roots , and LHDE has linearly independent particular solutions

and the general solution

2. Now we seek the general solution of the given equation in the form

By virtue of the formula (20) the system of linear equations in and its solution are

After integration

,

and the general solution of the given differential equation

.

Ex. 13. Solve Cauchy problem .

1. For corresponding [associated] homogeneous equation linearly independent particular solutions and the general solution

.

2. We seek the general solution of the given equation in the form

,

and by virtue of (20) we get the system of equations in

or

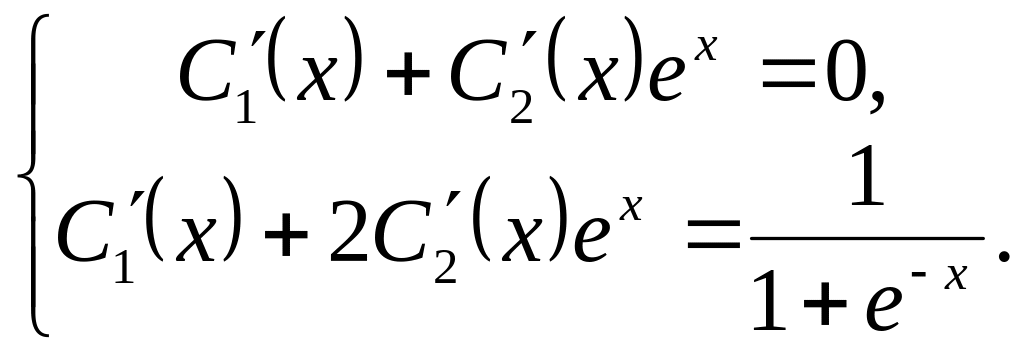
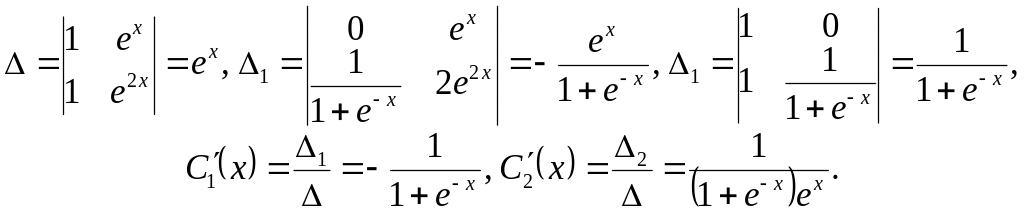
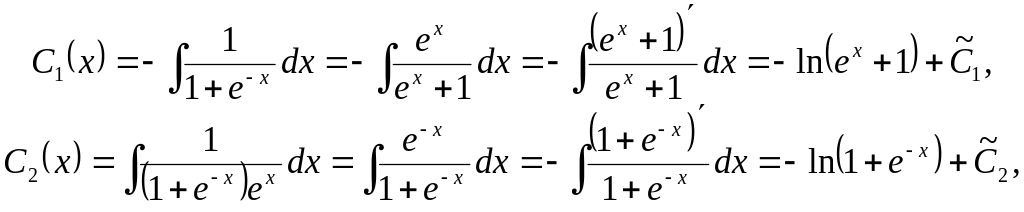
The general solution of the given differential equation is

.

3. Determination of values of with the help of the initial conditions.

The solution of Cauchy problem

.