26. Елементарні властивості невизначеного інтегралу. Таблиця основних інтегралів. Властивості невизначеного інтеграла

Визначимо ряд властивостей невизначеного інтеграла, виходячи з його визначення.

1. Диференціал від невизначеного інтеграла, рівний підінтегральному виразу, а похідна невизначеного інтеграла рівна підінтегральній функції:

Завдяки цій властивості правильність інтеграції перевіряється диференціюванням. Наприклад, рівність

2. Невизначений інтеграл від диференціала деякої функції рівний сумі цієї функції і довільної сталої:

3. Сталий множник можна виносити за знак інтеграла:

4. Невизначений інтеграл від алгебраїчної суми скінченного числа неперервних функцій рівний алгебраїчній сумі інтегралів від складових функцій:

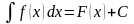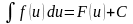5. (Інваріантність формули інтеграції). Якщо , то й , де 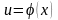– довільна функція, що має неперервну похідну.

Таким чином, формула для невизначеного інтеграла залишається справедливою незалежно від того, чи є змінна інтеграції незалежною змінною або будь-якою функцією від неї, що має неперервну похідну.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

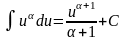
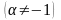
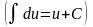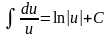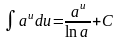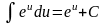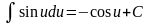
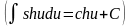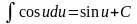
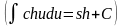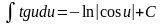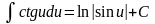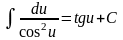
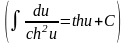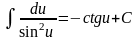
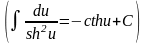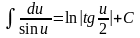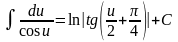27. Заміна змінної у невизначеному інтегралі.

Заміна змінної в невизначеному інтегралі проводиться за допомогою підстановок двох видів:

1) 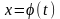, де 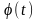- монотонна, неперервно диференційовна функція нової змінної t. Тоді . Формула заміни змінної в цьому випадку має вид

.

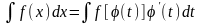2) 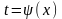, де t - нова змінна. Формула заміни змінної при такій підстановці має вид

.

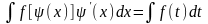28. Інтегрування частинами.

Нехай 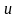і 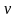- дві неперервно диференційовані функції від х. Тоді використавши формулу для диференціала добутку :

.

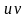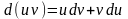Маємо 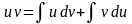або

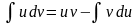. (1)

Ця формула називається формулою інтегрування частинами. За допомогою цієї формули знаходження інтеграла 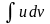зводиться до знаходження іншого інтеграла 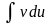; її застосування доцільно в тих випадках, коли останній інтеграл або простіше вихідного, або йому подібний.

При цьому за u береться така функція, яка при диференціюванні спрощується, а за dv - та частина підінтегрального виразу, інтеграл від якої відомий або може бути знайдений.

29. Розбиття відрізку. Інтегральна сума. Інтеграл Рімана.

Інтегр́ал Р́імана — одне з найважливіших понять математичного аналізу. Був уведений Бернгардом Ріманом в 1854 році, і є одною з перших формалізації поняття інтегралу.

Ріман формалізував поняття інтегралу, розроблене Ньютоном та Лейбницем, як площу фігури обмежену графіком функції та віссю абсцис. Для цього він розглянув фігури, які складаються з декількох вертикальних прямокутників отримані при розбитті відрізка (див. малюнок). Якщо при «подрібненні» розбиття існує границя, до якої збігаються площі таких фігур (інтегральні суми), то цю границю називають інтегралом Рімана функції на відрізку.

Через інтегральні суми

Нехай на відрізку   визначена дійсна функція дійсного аргументу   .

Розглянемо розбиття відрізка   — скінченна множина попарно різних точок відрізка. Це розбиття ділить відрізок  на n відрізків  .

Довжина найбільшого з них  , де  , зветься діаметром розбиття.

Розглянемо на кожному відрізку розбиття точку  . Інтегральною сумою зветься вираз  .

Якщо при прямуванні діаметра розбиття до нуля інтегральні суми збігаються до одного й того ж числа, незалежно від вибору  , то це число зветьсяінтегралом функції   на відрізку  , тобто

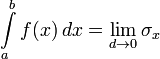
У цьому випадку, сама функція   називається інтегровною (за Ріманом) на  ; в протилежному випадку   є неінтегровною (за Ріманом) на відрізку  .

Через суми Дарбу

Суми Дарбу для розбиття на чотири інтервала: нижня (площа зеленого) і верхня (площа зеленого і сірого)

Нехай на відрізку   визначена дійсна функція дійсного аргументу  . Розглянемо довільне розбиття відрізка  .

Верхньою сумою Дарбу для розбиття   називається число

Відповідно, нижньою сумою Дарбу для розбиття   називається

Функція називається інтегровною за Ріманом, якщо існує дійсне число I для якого

У цьому випадку, за визначенням

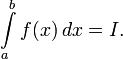
30.

Властивості інтеграла Рімана.

Властивості

• Якщо функція 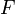  є первісною функції  , то інтеграл функції   на відрізку   можна обчислити за формулою Ньютона-Лейбніца: він дорівнює  .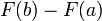

• Неперервна на відрізку функція інтегровна за Ріманом. Розривні функції можуть бути інтегровними, але можуть і не бути; прикладом функції, не інтегровної за Ріманом, є всюди розривна функція Діріхле.

• Обмеження: Якщо функція   інтегровна на відрізку  , то вона інтегровна й на меншому відрізку 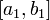 , де  .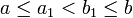

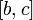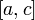• Якщо функція інтегровна на відрізку   та на відрізку  , то вона інтегровна і на відрізку  , і  .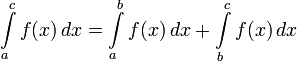

• Лінійність: Якщо функції   і 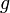  інтегровні, і 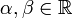 , то функція 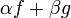  також інтегровна, і

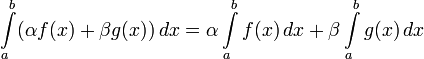
• Границя: Якщо інтегровні функції 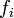  рівномірно збігаються на відрізку   до функції  , то   інтегровна, і

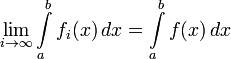
31. Основна теорема інтегрального числення

Якщо у функції   існує первісна  , то

Ця формула називається формулою Ньютона-Лейбніца, або основною формулою інтегрального числення. Вона дає практичний і зручний спосіб обчислення визначеного інтеграла за значеннями первісної на кінцях відрізку інтегрування. Багатомірні інтеграли обчислюються за допомогою теореми про зведення кратних інтегралів до повторного.

32.Заміна змінної у визначеному інтегралі. Приклади застосування визначеного інтегралу.

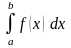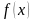Нехай треба обчислити інтеграл , де функція - неперервна на 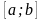. Якщо виконуються умови:

1. функція 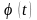неперервна разом із своєю похідною 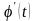на відрізку ;

2. , ;

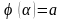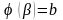3. при змінюванні 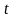на відрізку 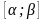значення функції 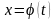не виходять за межі відрізка , то справедлива формула заміни змінної (або підстановки) у визначеному інтегралі:

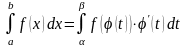(1.1)

.

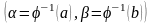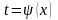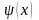Треба відзначити, що іноді набагато зручніше замість підстановки використовувати так звану «обернену» підстановку , де функція є строго монотонною і неперервно диференційовною на відрізку , а множиною її значень є відрізок . Тоді для неї існує обернена функція 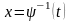, яка задовольняє переліченим вище умовам. Отже, в цьому випадку маємо:

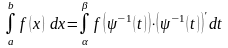(1.2)

.

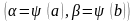Звернемо увагу на те, що на відміну від заміни змінної у невизначеному інтегралі, заміна змінної у визначеному інтегралі не потребує повернення до початкової змінної. Треба лише змінити межі інтегрування за формулами (1.1) або (1.2).

Застосування: Застосування визначеного інтеграла для обчислення площ фігур. Застосування визначеного інтеграла для обчислення об’ємів тіл. Застосування визначеного інтеграла в фізиці і техніці

Якщо фігура, площу якої треба знайти, обмежена графіками функцій f(x) (обмежує зверху) і g(x) (обмежує знизу), то для обчислення площі такої фігури треба обчислити інтеграл від різниці цих функцій на заданому проміжку.

Якщо криволінійна трапеція обмежена зверху різними функціями, то площа криволінійної трапеції дорівнює сумі площ криволінійних трапецій, обмежених зверху кожною з цих функцій.

Якщо фігура розміщена у від’ємній півплощині відносно осі абсцис, то її площу можна знайти як модуль визначеного відповідного інтеграла.

Об’єм тіла, утвореного обертанням навколо осі абсцис криволінійної трапеції, обмеженої зверху графіком неперервної невід’ємної функції, дорівнює визначеному інтегралу квадрата функції, помноженого на константу π.

Робота змінної сили вздовж осі абсцис на заданому проміжку дорівнює визначеному інтегралу від функції сили.

Шлях, що проходить тіло зі змінною швидкістю за проміжок часу, дорівнює інтегралу від функції швидкості.

Маса стержня із змінною густиною з заданою довжиною дорівнює визначеному інтегралу від функції густини.