
- •Лінійна алгебра
- •Визначники
- •Визначники другого і третього порядків
- •Розкладання визначника за елементами рядка або стовпця
- •1.3. Поняття про визначники вищих порядків.
- •Матриці
- •Основні означення.
- •Дії над матрицями.
- •Обернена матриця
- •Ранг матриці.
- •Системи лінійних рівнянь
- •Основні означення.
- •Розв‘язування систем лінійних рівнянь за формулами Крамера.
- •Матричний запис системи лінійних рівнянь та їх розв’язування
- •Розв‘язування системи лінійних рівнянь методом Гаусса.
- •Однорідні системи лінійних рівнянь.
Розв‘язування системи лінійних рівнянь методом Гаусса.
Одним з найпоширеніших методів розв‘язування систем лінійних рівнянь є метод послідовного виключення невідомих, або метод Гаусса.
Нехай задано
систему ![]() лінійних рівнянь
з
невідомими:
лінійних рівнянь
з
невідомими:
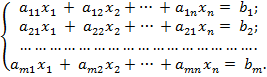
За допомогою елементарних перетворень цю систему приводять до системи вигляду:
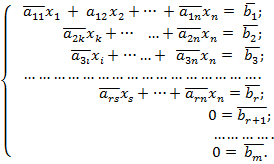
Таку систему рівнянь називають східчастою або трапецієподібною.
Дослідимо цю систему.
Якщо система містить рівняння виду
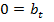 або
або
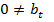 ,
то вона несумісна.
,
то вона несумісна.Якщо система не містить рівнянь виду ( ), то вона має безліч розв‘язків.
Назвемо невідомі
![]() основними, а всі інші – вільними. Надаючи
вільним невідомим довільні значення і
підставляючи їх у рівняння системи, з
основними, а всі інші – вільними. Надаючи
вільним невідомим довільні значення і
підставляючи їх у рівняння системи, з
![]() -го рівняння знайдемо
-го рівняння знайдемо ![]() . піднімаючись угору по системі, знайдемо
всі останні невідомі. Оскільки вільні
невідомі можуть набувати будь – яких
значень, то система має безліч розв‘язків.
. піднімаючись угору по системі, знайдемо
всі останні невідомі. Оскільки вільні
невідомі можуть набувати будь – яких
значень, то система має безліч розв‘язків.
Якщо
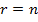 ,
то система має трикутний вигляд і
вільних невідомих немає. Система має
єдиний розв‘язок.
,
то система має трикутний вигляд і
вільних невідомих немає. Система має
єдиний розв‘язок.
Приклад.
Розв‘язати систему рівнянь методом Гаусса.
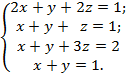
При розв‘язуванні системи лінійних рівнянь методом Гаусса зручніше приводити до трикутного чи трапецієподібного вигляду не саму систему, а розширену матрицю цієї системи, тобто матрицю, утворену приєднанням до матриці її коефіцієнтів стовпця вільних членів. Виконуючи над рядками розширеної матриці елементарні перетворення, приходимо до розв‘язку системи.
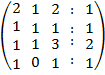 {
зробимо
коефіцієнт
{
зробимо
коефіцієнт ![]() рівним
одиниці, тобто поміняємо місцями перший
та другий рядки }
=
рівним
одиниці, тобто поміняємо місцями перший
та другий рядки }
=
=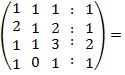 {
помножимо
послідовно перший рядок на (-2), (-1), (-1) та
додамо відповідно до 2, 3, 4 рядків }
=
{
помножимо
послідовно перший рядок на (-2), (-1), (-1) та
додамо відповідно до 2, 3, 4 рядків }
=
=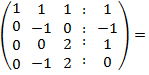 {
перший та
третій рядки залишимо без змін, а другий
помножимо на (-1) та додамо до четвертого
} =
{
перший та
третій рядки залишимо без змін, а другий
помножимо на (-1) та додамо до четвертого
} =
=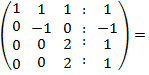 {
перший та
другий рядки не змінюємо, а третій
помножимо на (-1) та додамо до четвертого
} =
{
перший та
другий рядки не змінюємо, а третій
помножимо на (-1) та додамо до четвертого
} =
=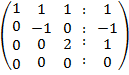 .
.
Отже, система еквівалентна системі трикутного вигляду
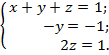 І має
єдиний розв‘язок x
І має
єдиний розв‘язок x![]()
Однорідні системи лінійних рівнянь.
Однорідна система лінійних рівнянь з невідомими має вигляд:
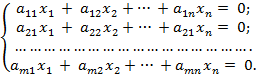
Ця система завжди
має нульовий розв‘язок: ![]()
Ненульовий
розв‘язок, якщо він є, можна знайти
методом Гаусса. Якщо ![]() і визначник
системи дорівнює нулю,то однорідна
система має безліч ненульових розв‘язків.
і визначник
системи дорівнює нулю,то однорідна
система має безліч ненульових розв‘язків.
Покажемо, що для однорідної системи трьох рівнянь з трьома невідомими можна знайти загальні формули, що виражають ненульові розв‘язки через коефіцієнти системи.
Розглянемо систему
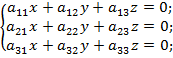
Якщо визначник
системи системи ![]() то система має єдиний нульовий розв‘язок.
Дійсно,
то система має єдиний нульовий розв‘язок.
Дійсно, ![]() ,
тому за формулами Крамера
,
тому за формулами Крамера ![]()
Покажемо, що коли
визначник ![]() то система має безліч розв‘язків.
Розглянемо такі випадки.
то система має безліч розв‘язків.
Розглянемо такі випадки.
Припустимо, що у визначнику існує принаймні один відмінний від нуля мінор другого порядку. Нехай, наприклад,
![]()
Візьмемо ті рівняння системи, що містять відмінний від нуля мінор і запишемо їх у вигляді
![]()
Оскільки визначник системи відмінний від нуля, то за формулами Крамера
![]() де
де
![]() ;
; ![]()
![]()
Оскільки ![]() може
набувати будь – яких дійсних значень,
покладемо
може
набувати будь – яких дійсних значень,
покладемо ![]() ,
де
,
де ![]() – довільне дійсне число, тоді
– довільне дійсне число, тоді
![]() ;
; ![]()
![]() .
.
Нехай тепер визначник початкової системи і всі його мінори другого порядку дорівнюють нулю. Тоді система зводиться до одного рівняння з трьома невідомими. Надаючи двом невідомим довільних значень, знаходять відповідно їм третє невідоме.
Приклад.
Розв‘язати систему рівнянь
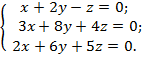
Визначник системи
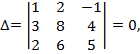 тому система невизначена.
тому система невизначена.
Візьмемо перше і друге рівняння системи. Ці рівняння містять відмінний від нуля мінор другого порядку
![]()
Тоді ранг цієї
системи ![]() Кількість вільних невідомих
Кількість вільних невідомих ![]() Нехай це буде z
Нехай це буде z
![]()
Виберемо величину
z
у формі ![]() де t
– довільне число. Із двох перших рівнянь
системи знаходимо:
де t
– довільне число. Із двох перших рівнянь
системи знаходимо:
![]()
Остаточно ![]()
