
- •1.Лінійні операції над векторами та їх властивості. Скалярний добуток векторів його властивості та застосування.
- •Афінна система координат. Координати точок. Знаходження координат вектора
- •Полярна система координат. Перехід від полярної до прямокутної системи координат і навпаки
- •3. Пряма лінія в афінній системі координат
- •4. Рівняння площини в афінній системі координат
- •5. Пряма лінія у просторі
- •Взаємне розташування двох прямих у просторі
- •Взаємне розташування прямої і площини
- •6. Метричні задачі на пряму і площину
- •Гіпербола.
- •8.Еліпсоїд, гіперболоїди, параболоїди. Дослідження їх форм методом перерізів, їх побудова.
- •9. Циліндричні та канонічні поверхні, їх властивості. Класифіфкація поверхонь 2-го порядку.
- •10. Рух 1 і 2 роду. Класифікація рухів площини та їх аналітичне задання. Групи рухів та їх підгрупи.
- •11. Перетворення подібності. Гомотетія. Аналітичне задання подібності. Група подібності та її властивості.
- •12. Група афінних перетворень площини і її підгрупи.
- •13. «Начала» Евкліді. Проблема 5-го постулату. Огляд аксіоматики гільберта евклідової геометрії.
- •1. Аксіоми належності та наслідки з них :
- •2. Аксіоми порядку і деякі наслідки:
- •5. Аксіома паралельності (Плейфера).
- •14. Аксіоматика Вейля. Доведення несуперечності та повноти аксіоматики Вейля.
- •15. Геометрія Лобачевского. Основні факти. Несуперечливість системи аксіом площини Лобачевского незалежність V постулату.
- •16. Різні види рівняння кривої у просторі. Тригранник Френе.
- •17. Кривина та скрут просторової кривої. Формули Френе.
- •18. Поверхні в евклідовому просторі. Криволінійні координати на поверхні. Дотична площина і нормаль поверхні.
- •19. Перша та друга квадратичні форми поверхні та їх застосування.
- •20. Топологічні простори та їх основні властивості. Приклади. Предмет топології.
- •21.Ейлерова характеристика поверхні.Орієнтовні та неорієнтовні двовимірні многовиди. Рід многовида та число його контурів
- •22. Існування 5 типів правильних многогранників. Топологічна класифікація многогранників
4. Рівняння площини в афінній системі координат
Вектор, який лежить на площині або паралельний до неї, наз. направляючим вектором площини.
Площину
в афінній с-мі коор. (О,
,
,![]() )
можна задати двома направляючими
векторами (неколінеарними)
і
точкою, або трьома точками, які не лежать
на одній прямій.
)
можна задати двома направляючими
векторами (неколінеарними)
і
точкою, або трьома точками, які не лежать
на одній прямій.
1. Рівняння площини, заданої двома направляючими векторами і точкою.
Нехай
площина π задана неколінеарними
направляючими векторами
=(α1,β1,γ1)
і
![]() =(α2,β2,γ2),
та точкою М0(x0,y0,z0).
Виберемо на площині ще одну довільну
точку М(x,y,z).
Розглянемо вектор
=(α2,β2,γ2),
та точкою М0(x0,y0,z0).
Виберемо на площині ще одну довільну
точку М(x,y,z).
Розглянемо вектор
![]() =(x-x0,
y-y0,
z-z0).
Оскільки т.М
належить площині то вектори
,
та
компланарні, отже за теоремою 9:
=(x-x0,
y-y0,
z-z0).
Оскільки т.М
належить площині то вектори
,
та
компланарні, отже за теоремою 9:
![]() =0
(33)
=0
(33)
2. Рівняння площини, заданої трьома точками.
Нехай
площина задана трьома точками, які не
лежать на одній прямій М1(x1,y1,z1),
М2(x2,y2,z2),
М3(x3,y3,z3).
Тоді можна скористатися рівнянням (33),
поклавши
=![]() ,
=
,
=![]() ,
а М0=М1.
Отримаємо:
,
а М0=М1.
Отримаємо:
![]() =
0 (34)
=
0 (34)
3. Рівняння площини у відрізках (на осях):
Нехай
площина відтинає на осях координат
відрізки a,
b
і c
відповідно. Тоді вона проходить через
точки А(а,0,0),
В(0,b,0) і
С(0,0,с).
Використавши р-ня (34), маємо:![]() =0,
або після елементарних перетворень:
+
+
=0,
або після елементарних перетворень:
+
+![]() =1.
(35)
=1.
(35)
Відмітимо, що a, b і c направлені відрізки, тому вони можуть бути і від’ємні.
4. Параметричні рівняння площини:
Нехай площина π задана направляючими векторами =(α1,β1,γ1), =(α2,β2,γ2) і точкою М0(x0,y0,z0). Виберемо на площині ще одну довільну т.М(x,y,z). Розглянемо вектор: =(x-x0,y-y0,z-z0). За теор4 =λ +μ . Перейшовши до координат, отримаємо:
x-x0=λα1+μα2 x=λα1+μα2+x0,
y-y0=λβ1+μβ2, або y=λβ1+μβ2+y0, (36)
z-z0=λγ1+μγ2, z=λγ1+μγ2+z0,
де
λ, μ параметри
(λ,μ
![]() R).
R).
5. Загальне рівняння площини:
Всі отримані нами рівняння площини – це рівняння першого степеня з трьома змінними, а тому їх можна записати загальним рівнянням Ax+By+Cz+D=0. (37)
Теор16. Множина точок простору, координати яких в афінній с-мі коор. задовольняють р-ня (37), де А, В і С не рівні нулю одночасно, являє собою площину, причому =(-В,А,0) і =(-С,0,А) – направляючі вектори цієї площини.
Доведення:
Розглянемо
р-ня (37), де А,
В
і С![]() 0
одночасно. Його можна записати у вигляді:
0
одночасно. Його можна записати у вигляді:
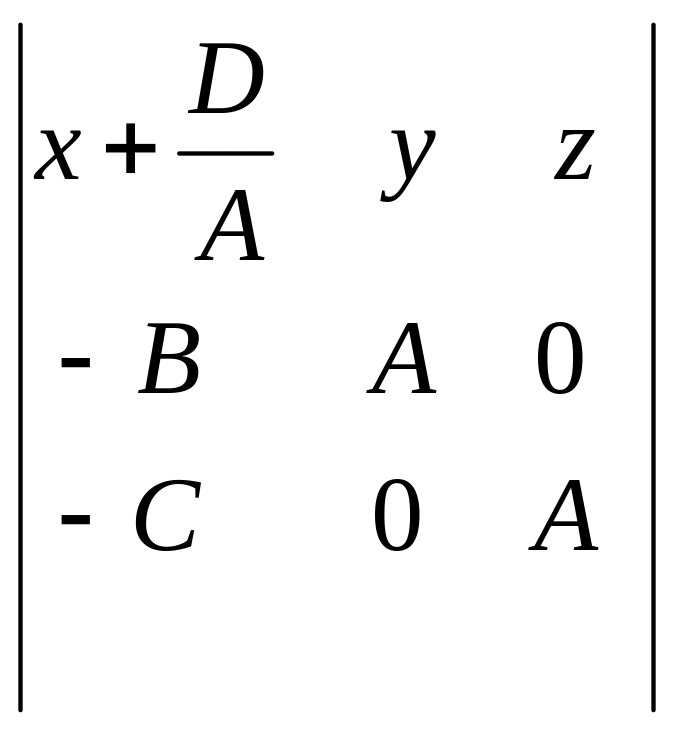 = 0.
Отже, р-ня (37) рівносильне р-ню площини
вигляду (33), заданої 2ма направляюч.
векторами
=(-В,А,0),
=(-С,0,А)
і т.М(-
= 0.
Отже, р-ня (37) рівносильне р-ню площини
вигляду (33), заданої 2ма направляюч.
векторами
=(-В,А,0),
=(-С,0,А)
і т.М(-![]() ;0;0).
;0;0).
Площина в прямокутній системі координат
Так як прямокутна с-ма коор. (O, , , ) є частковим випадком афінної, то в ній можна використовувати всі отримані раніше р-ня (33)–(37) площини.
Нормальним вектором площини наз. будь-який вектор, перпендикулярний до цієї площини.
У прямокутній с-мі коор. можна отримати ще два р-ня площини: за точкою і нормальним вектором, та нормальне р-ня.
6. Рівняння площини за точкою і нормальним вектором.
Нехай
в прямокутній с-мі коор. (O,
,
,
)
площину
задано
точкою Н0(x0,y0,z0)
і нормальним вектором
=(А,В,С).
Візьмемо на площині довільну точку
Н(x,y,z). Тоді
![]() =(x-x0, y-y0, z-z0).
Так як вектор
=(x-x0, y-y0, z-z0).
Так як вектор
![]() перпендикулярний до вектора
,
то їх скалярний добуток дорівнює нулю,
отже, за теор 8: А(x-x0)+В(y-y0)+С(z-z0)=0
(38)
перпендикулярний до вектора
,
то їх скалярний добуток дорівнює нулю,
отже, за теор 8: А(x-x0)+В(y-y0)+С(z-z0)=0
(38)
Нормальне рівняння площини.
Нехай
площина задана в прямокутній с-мі коор.
одиничним нормальним вектором
![]() і відстанню r
від початку координат до площини. Нехай
Н
– основа перпендикуляра, опущеного із
початку координат на площину. Знайдемо
координати т.Н.
Так як координатами точки назвали
координати її радіус-вектора, то знайдемо
координати вектора
і відстанню r
від початку координат до площини. Нехай
Н
– основа перпендикуляра, опущеного із
початку координат на площину. Знайдемо
координати т.Н.
Так як координатами точки назвали
координати її радіус-вектора, то знайдемо
координати вектора
![]() .
Отже, координати точки
Н (r cosa1, r cosa2, r cosa3).
Використавши р-ня (38), отримаємо нормальне
р-ня: cosa1(x-rcosa1)+cosa2(y-rcosa2)+cosa3(z-rcosa3)=0
або
.
Отже, координати точки
Н (r cosa1, r cosa2, r cosa3).
Використавши р-ня (38), отримаємо нормальне
р-ня: cosa1(x-rcosa1)+cosa2(y-rcosa2)+cosa3(z-rcosa3)=0
або
x cosa1+y cosa2+z cosa3 –r =0 (39).
Відстань від точки до площини
Нехай
дана точка М0(x0,y0,z0),
а
площина задана загальним рівнянням
Ax+By+Cz+D=0. Нормальний вектор площини
![]() =(А,В,С).
Розглянемо такий вектор
=(А,В,С).
Розглянемо такий вектор
![]() ||
,
що його початок – точка Н(x,y,z) належить
площині. Тоді відстань d
від точки М0(x0,y0,z0)
до площини буде дорівнювати довжині
вектора |
|.
=(x – x0 ,
y – y0 ,
z – z0).
Знайдемо скалярний добуток:
·
=|
|·|
|
cosφ. Так як кут φ між векторами
і
може бути 0˚, або 180˚, то cosφ=
||
,
що його початок – точка Н(x,y,z) належить
площині. Тоді відстань d
від точки М0(x0,y0,z0)
до площини буде дорівнювати довжині
вектора |
|.
=(x – x0 ,
y – y0 ,
z – z0).
Знайдемо скалярний добуток:
·
=|
|·|
|
cosφ. Так як кут φ між векторами
і
може бути 0˚, або 180˚, то cosφ=![]() 1.
Отже,
·
=
|
||
|.
Звідки
1.
Отже,
·
=
|
||
|.
Звідки
d
= |
|=![]() =
=
![]() .
.
Оскільки точка Н належить площині, то її координати задовольняють рівняння (37), тому –Ax–By–Cz=D і
d
=
![]() (40).
(40).
