1.Лінійні операції над векторами та їх властивості. Скалярний добуток векторів його властивості та застосування.

Сумою двох векторів = і = наз. вектор = , який є діагоналлю паралелограма, побудов. на векторах і (рис.1).

+ = + = = . Так як = , то + = .

П равило додавання векторів, яке визначається цією формулою, називається правилом трикутника.

Властивості додавання:

1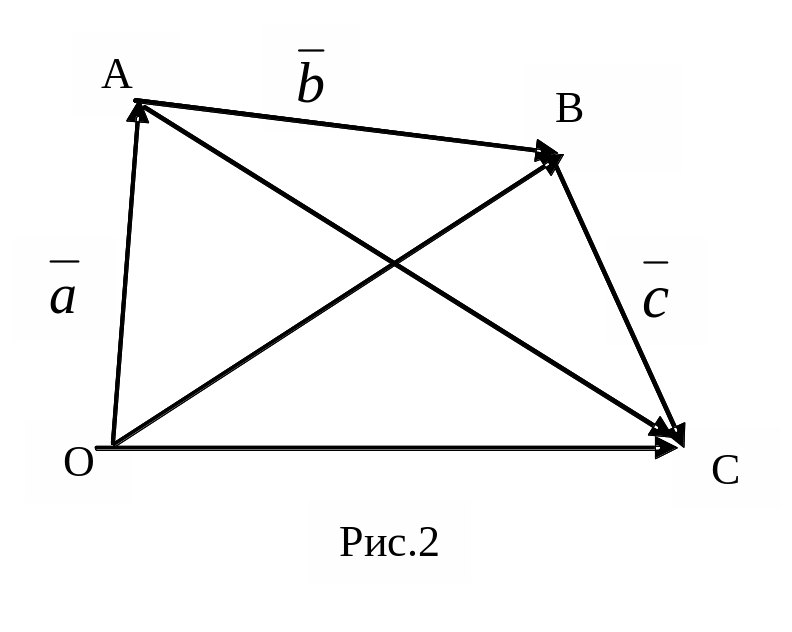 . Для будь-яких векторів , і : +( + )=( + )+ (асоціатив. закон додавання).

Доведення: (рис.2).

+( + )= +( + )= + = ,

( + )+ =( + )+ = + = .

2. Для будь-яких векторів і : + = + ( комутатив. закон додавання ).

Доведення: + = + = (рис.1), + = + = .

3. Існує вектор , такий, що для будь-якого : + = .

Доведення: Нехай = , тоді за правилом трикутника = , так як + = + = = .

4. Існує вектор ^′_, такий, що для будь-якого вектора : + ^′ = .

Доведення: Нехай = ; тоді + = = , отже, ^′= (це вектор протилежний до ).

Різницею двох векторів  –  наз. такий вектор , що + = .

Р ізниця будь-яких векторів і завжди існує і визначається однозначно, так як – = +(– ). Вектор – існує і визначається однозначно, сума двох векторів і (– ) існує і визначається однозначно. Отже, щоб від вектора відняти вектор потрібно до вектора додати вектор – (рис.3).

– = – = + = + = = .Маємо: – = (рис.3).

Добутком вектора на дійсне число λ називається такий вектор , для якого виконуються умови: 1. | |=| λ | | |– довжина вектора ; 2. ↑↑ – коли λ >0; 3. ↑↓ – коли λ <0;

Властивості: Для будь-яких дійсних чисел α і β та векторів , мають місце рівності: 1. 1· = ; (–1)· = –  ;

2. α·( + ) = α· +α· ;

3. (α+β)·  =  α· +β· ;

4. α·(β· ) = (α·β)· .

Доведення:

1. Властивість випливає з означення добутку вектора на число.

2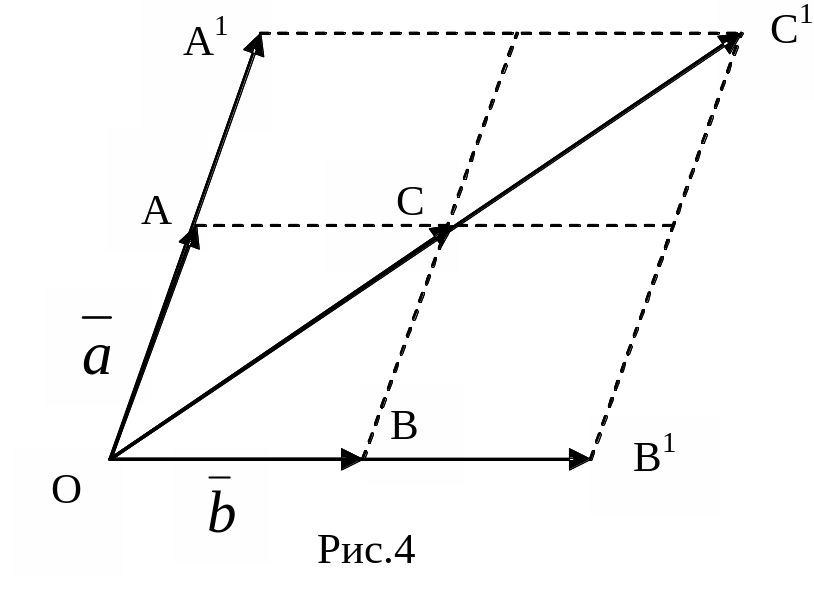 .α·( + )=α·( + )=α· = (рис.4).

α· +α· =α· +α· = + = (рис.4).

Отже, ми отрим. гомотетію з центром в т.О та коефіцієнтом α. При гомотетії паралелограм ACBO перейшов у паралелограм A C B O , діагональ OC перейшла в OC .

3. Справедливість третьої властив. випливає з того, що вектори α і β колінеарні. Їх додавання фактично зводиться до додавання чисел α·  і β·  та побудови вектора отриманої довжини, який колінеарний вектору .

4. Очевидно, що вектори α(β і (αβ) співнаправлені, так як в обох випадках добуток чисел α і β має однаковий знак. Покаж., що і модулі їх рівні. Дійсно, за означенням добутку вектора на число отримаємо:

│α·(β· )│=│α│∙│(β· )│=│α│∙│β│∙│ │.

│(α·β)· │=│(α·β)│∙│ │=│α│∙│β│∙│ │.

Відклад. ненульові вектори і від точки О: = , = (рис.7). Кут АОВ називається кутом між векторами і і позначається ( ˆ ) = α. Кут між векторами вибирається меншим або рівним  .

Для розв’яз. метричних задач використав. Ортонормов. базис ,  ,  , де і всі кути між цими векторами рівні 90⁰

Скалярним добутком двох ненульових векторів і наз. число яке = модулів цих векторів на косинус кута між ними (познач. ∙ = | |∙| |∙cosα).

Скалярний добуток нуль-вектора і довільн. вектора покладається рівним нулю.

З означ. скалярного добутку отримаємо формулу для знаходження косинуса кута між векторами: cos ( ˆ ) = (4)

Теор8 Скалярний добуток векторів =(а₁,а₂ ,а₃ ), =(b₁,b₂ ,b₃ ), заданих в ортонормов. базисі пр-ру, виражається формулою: ∙ =а₁b₁+а₂b₂+а₃b₃ (5)

Доведення: Запишемо розклади даних векторів по базису:

= а₁  + а₂  + а₃  і = b₁ + b₂ + b₃ .

Тоді ∙ = (а₁ + а₂ + а₃ )∙(b₁ + b₂ + b₃ )=

= а₁ b₁ ( ∙ )+ а₁ b₂ ( ∙ )+ а₁ b₃ ( ∙ )+ а₂ b₁ ( ∙ )+ а₂ b₂ ( ∙ )+

+ а₂ b₃ ( ∙ )+ а₃ b₁ ( ∙ )+ а₃ b₂( ∙ )+ а₃ b₃ ( ∙ ). А так як скалярні добутки ∙ = ∙ = ∙ =1, а ∙ = ∙ = ∙ =0 , то отримаємо, що ∙ = а₁b₁+а₂ b₂+а₃ b₃.

Наслід9. Вектори =(а₁, а₂ , а₃ ); =(b₁, b₂ , b₃ ) задані в ортонормов. базисі простору, взаємно перпендикулярні ↔, коли а₁ b₁+а₂ b₂+а₃ b₃ = 0.

Розгул. скалярний добуток вектора на себе:  = | |² . наз. скалярним квадратом вектора і познач. ². Звідси отрим. ф-лу для обчислення модуля вектора за його координат.: | | =  =

Наслід10. Косинус кута α між ненульовими векторами =(а₁, а₂, а₃) і =(b₁, b₂, b₃), заданими в ортонормованому базисі, визначається формулою: cos α =  .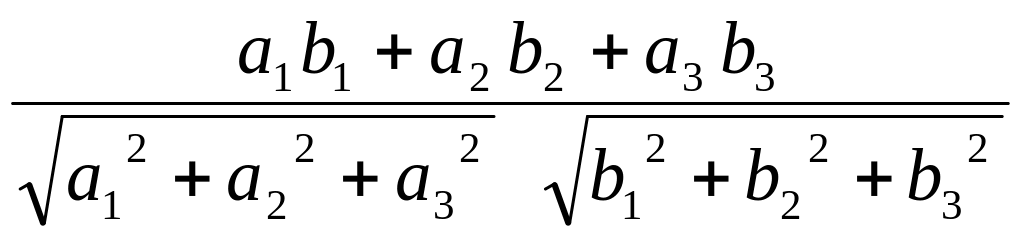

Властивості скалярного добутку:

1. ∙ =  ∙ (комутативність).

2. (α  )· =α ( · ) (скаляр. множник можна винос. за знак скаляр. добутку).

3. ( + )· = · + · (дистрибутивність).

Доведення.

1. Властивість випливає з означення скалярного добутку.

2. Нехай в ортонормов. базисі вектори і мають координати = (а₁, а₂, а₃), = (b₁, b₂, b₃). Тоді за наслід8 вектор α·  = (α а₁, α а₂, α а₃) і за теор8

(α  )· = α а₁b₁+α а₂ b₂+α а₃ b₃ = α (а₁b₁+а₂ b₂+а₃ b₃ ) = α ( · ).

3. Нехай в ортонормованому базисі вектори , і мають координати: = (а₁, а₂, а₃), = (b₁, b₂, b₃),  =(c₁, c₂, c₃ ). За наслід6 вектор +  = (а₁ +b₁ , а₂ +b₂ , а₃ +b₃ ) і ( + ) · = (а₁ +b₁ ) c₁ +(а₂ +b₂ ) c₂ +(а₃ +b₃ ) c₃  =

= (а₁ c₁ +а₂ c₂ +а₃ c₃ ) + (b₁ c₁ +b₂ c₂ +b₃ c₃ ) = ·

2. Векторний та мішаний добутки векторів, їх властивості та застосування.

Векторним добутком двох векторів та наз. вектор , для якого виконуються умови: 1. | | дорівнює площі паралелограма побудованого на векторах і . (| |=| || | sin( ˆ ) ). 2. перпендикулярний як з так і з . 3. Якщо та не колінеарні, то вектор має такий напрямок, що впорядкована трійка векторів , , має праву орієнтацію (рис. 16).

Векторний добуток позначають =[ , ] або = × .

З означ. слідує: якщо вектори колінеарні, то їх векторний добуток рівний нулю.

Теор10. Для того, щоб вектори були колінеарними необхідно і досить, щоб їх векторний добуток дорівнював нулю.

Властивості:

1. [ , ]= - [ , ] (антикомутативність).

2. α [ , ]=[α  , ]=[ ,α  ] (винесення скалярного множника).

3. [ , + ]=[ , ]+[ , ], [ + , ]=[ , ]+[ , ] (дистрибутивність).

Доведемо перші дві властивості.

1. Якщо вектори і колінеарні, то [ , ] = [ , ] =0 і властив. доведена. Нехай та неколінеарні. Тоді вектори [ , ] і [ , ] мають однакові модулі, але протилежно направлені, оскільки трійки векторів , ,[ , ]  і , [ , ] мають протилежну орієнтацію. Це означає, що [ , ]= -[ , ].

2. Доведемо першу рівність. Якщо α=0, то рівність очевидна. Нехай α  0. Тоді |[α  , ]| = |α || | sin(α ˆ ) = α | || | sin( ˆ ) = =|α[ , ]|. Оскільки α  0, то очевидно, що вектори α[ , ] і [α  , ] співнаправлені. Якщо α  0, то як і раніше можна показати, що |[α  , ]|=|α[ , ]|. А напрямок вектора [α  , ] протилежний до напрямку [ , ], але такий же як вектора α[ , ]. Отже, α[ , ]=[α  , ]. Аналогічно доводиться друга рівність.

Теор11. Якщо вектори та в с-мі коор. (O,  , , ) мають відповідно координати =(a₁,a₂,a₃), =(b₁,b₂,b₃), то їх векторний добуток знаходиться за формулою:[ , ]= (21)

Доведення. Запиш. розклади даних векторів по базису: = a₁  +a₂ +a₃ , =b₁  +b₂ +b₃ . Тоді, користуючись властивостями, отримаємо:

[ , ]=a₁  +a₂ +a₃ , b₁  +b₂ +b₃ =

= a₁b₂  , +a₁b₃ , +a₂b₁ , +a₂b₃ , +a₃b₁ , +a₃b₂ , . Так як  , = ,   ,  = ,  ,  =  , то отримаємо [ , ]=(a₂b₃ - -a₃b₂) +(a₃b₁ - a₁b₃) +(a₁b₂ - a₂b₁ ) = + + .

Мішаним добутком векторів , і (позначається ( , , )) наз. скалярний добуток вектора на векторний добуток векторів та :

[ , ]=( , , )=[ , ] .

Т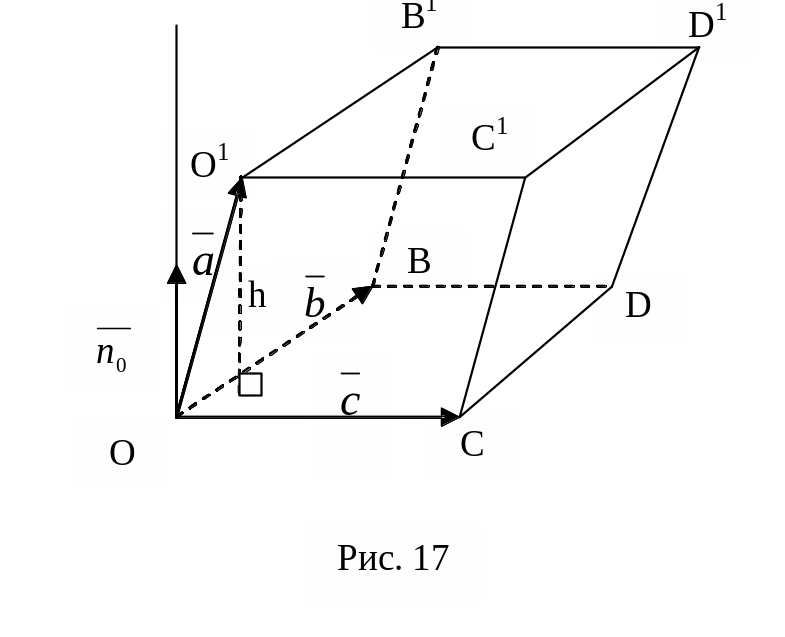 еор12 (Геометричний зміст мішаного добутку).

Якщо вектори , , не компланарні, то модуль мішаного добутку |( , , )| дорівнює об’єму паралелепіпеда побудованого на векторах , , (рис.17).

Доведення:

Розглянемо векторний добуток [ , ]. Позначимо одиничний вектор, співнаправлений з [ , ], а φ – кут між ним і вектором . Враховуючи, що [ , ]=|[ , ]| ∙ = S_OBDC  , отримаємо: ( , , ) = ∙[ , ] = ∙ S_OBDC  = S_OBDC  ∙ = S_OBDC | || | cosφ == S_OBDC (+/- h) = +/- V (оскільки вектори і можуть утворювати як гострий кут (рис.17) так і тупий (вектор направлений вниз), то cosφ може бути як додатній, так і від’ємний). Отже V=|( , , )|. Теорему доведено.

Теор13. Якщо вектори , та мають координати =(a₁,a₂,a₃), =(b₁,b₂,b₃), =(с₁,с₂,с₃) то мішаний добуток цих векторів дорівнює визначнику 3-го порядку, складному з їх координат: ( , , )=

Доведення: Знайдемо векторний добуток векторів і . Згідно формули (21): ∙[ , ] = . Тоді

( , , ) = [ , ]= а₁  +а₂  + а₃ = .

Мішаний добуток векторів рівний визначнику третього порядку, а значить має такі ж властивості, як і визначники.

Властивості:

1. Якщо три вектори компланарні то мішаний добуток дорівнює нулю.

2. Мішаний добуток додатній, якщо впорядкована трійка векторів , , має додатну орієнтацію і навпаки.

3. При перестановці місцями двох векторів у мішаному добутку, знак визначника змінюється на протилежний, а його абсолютна величина не змінюється: .

4. Число можна виносити за знак мішаного добутку:

α ( , , )=(α , , )=( ,α , )=( , ,α ).

5. Якщо один з векторів являється сумою інших, то:

( + , , )=( , , )+( , , ).

3. 4.