§12. Полные и неполные изображения.

Пусть  – плоскость изображений. Говорим, что точка M; ¯ задана, если задана её аксонометрическая проекция и одна из вторичных проекций, например, M₃. Прямая a считается заданной, если заданы две её точки или её аксонометрическая и вторичная проекции. Плоскость считается заданной, если заданы элементы, которые её однозначно определяют (например, три точки, которые не принадлежат одной прямой, прямая и точка или две прямые).

П усть на плоскости  дано изображение F некоторой фигуры F; ¯. Это изображение называется полным, если к нему можно присоединить изображение R аффинного репера так, что

все прямые, точки и плоскости, которые определяют фигуру F, будут заданы.

П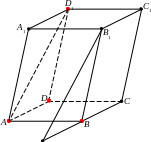 ример 1. Данное изображение параллелепипеда является полным. Если к нему присоединить изображение R ={A, B, D, A₁} аффинного репера, то все вершины будут заданы, т.е. у каждой вершины можно указать аксонометрическую и вторичную проекции. Например, у вершины A; ¯ – (A, A), у B₁ – (B₁, B).

О казывается свойство изображения быть полным или неполным не зависит от выбора присоединённого репера (без доказательства). Если в последнем примере выбрать за изображение репера R ={A, B, D, D₁}, то вторичная проекция точки B₁ будет отсутствовать, но её можно построить. Для этого нам нужно провести через B₁ прямую параллельную AD₁ до пересечения с прямой BC (самостоятельно обоснуйте, почему).

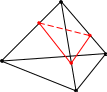
Пример 2. Данное изображение шестигранника не является полным. Если к нему присоединить изображение R = ={A, B, C, S} аффинного репера, то вершины A; ¯, B; ¯, C; ¯, S; ¯ будут заданы, а D; ¯ – нет. У неё есть аксонометрическая проекция D, а в качестве вторичной проекции мы можем взять любую точку D₃, принадлежащую прямой l||AS, проходящей через D, даже если эта точка будет находиться за пределами треугольника ABC. На следующем чертеже мы выбрали точку K, а точка L потом однозначно достраивается.

К оличество точек, которые необходимо добавить к чертежу, для того, чтобы изображение стало полным, называется коэффициентом неполноты изображения. В последнем примере он равен 1.

П ример 2. Данное изображение тетраэдра и прямой имеет коэффициент неполноты равный 2. Для того чтобы оно стало полным, необходимо добавить точки пересечения прямой с гранями пирамиды (и соответственно, часть линии сделать пунктирной). Мы добавляем точки M и N, а точки M_o и N_o однозначно достраиваются.

Задачи на построение на неполном изображении не имеют единственного решения. Недостающие элементы можно добавлять произвольно.

§13. Построение сечений многогранников. Метод соответствия.

В дальнейшем, ради удобства изложения, мы не будем отличать оригинал от изображения. Например, если A – изображение вершины многогранника, то мы называем её вершиной.

Определение. Плоскость называется секущей для многогранника, если по обе стороны от этой плоскости есть точки этого многогранника. Каждая грань многогранника пересекается секущей плоскостью по отрезку. Объединение этих отрезов образует многоугольник, который называется сечением многогранника.

Например, сечением тетраэдра может быть треугольник или четы­рёхугольник. Поскольку граней всего 4, то других вариантов быть не может.

Сечением куба может быть трех-, четырёх-, пяти- или шестиугольник. Поскольку граней всего 6, то других вариантов быть не может.

З адача 1. Дано изображение треугольной призмы ABCA₁B₁C₁ и трёх точек M, N, P, которые лежат соответственно на ребре AA₁ и гранях ABB₁A₁, BCC₁B₁. Построить сечение призмы плоскостью, проходящей через M, N, P.

Решение. На чертеже данные точки выделены крупно. Если данному изображению добавить изображение R ={A, B, C, A₁} аффинного репера, то все точки будут заданы. Для примера мы показали, как построить вторичную проекцию N₃ точки N. Поэтому изображение является полным и задача имеет единственное решение.

Точки M и N принадлежат одной грани ABB₁A₁, поэтому они принадлежат одной стороне сечения. Проводим через них

прямую линию до пересечения с ребром, но только с тем, которое принадлежит данной грани (на данном чертеже это ребро BB₁). Получим точку X. Точки X и P принадлежат одной грани ABB₁A₁. Проводим через них прямую линию до пересечения с ребром, которое принадлежит данной грани. Получим точку Y. Точки Y и M принадлежат одной грани. Поэтому можем соединить их отрезком. Треугольник MXY – искомое сечение.

В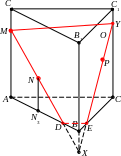 озможны варианты, когда MN пересечёт ребро AB, а не BB₁. В этом случае нам нужно найти точку, которая лежит в плоскости одной грани с точкой P. Для этого мы найдём точку X, которая получается в пересечении прямой MN с продолжением ребра BB₁. Построение тогда записывается следующим образом.

1. MNBB₁=X, MNAB=D;

2. XPCC₁=Y, XPBC=E;

3. MDEY – искомое сечение.

Точно также точка Y может оказаться на продолжении ребра CC₁. Этот случай разберите самостоятельно.

Не всегда среди данных точек можно найти две, лежащие в одной грани. Задача 2 из §11 даёт нам способ нахождения точки, принадлежащей секущей плоскости, на любом из вертикальных рёбер призмы (либо на продолжении ребра). Прежде, чем продолжать чтение, внимательно изучите эту задачу ещё раз.

З адача 2. Дано изображение треугольной призмы ABCA₁B₁C₁ и трёх точек M, N, P, которые лежат соответственно на ребре СС₁ и гранях ABB₁A₁, BCC₁B₁. Построить сечение призмы плоскостью, проходящей через M, N, P.

Решение. Мы будем искать точку X, в которой секущая плоскость пересекает ребро BB₁. Нам известна её вторичная проекция B=X₃ и даны три точки, через которые проходит секущая плоскость. Сначала построим вторичные проекции этих точек M₃, N₃, P₃. Это очевидное действие мы, как правило, в процесс построения включать не будем. Далее, точно так же, как и в задаче 2 из §11 строим:

1. M₃BN₃P₃=Y₃;

2. l||AA₁, Y₃l;

3. lN₃P=Y;

4. MYBB₁=X.

Действия под номерами 2 и 3 в дальнейшем будем записывать так: поднимаем точку Y₃ до прямой NP и получаем Y. Дальнейшие действия смотрите в задаче 1. Мы их записывать не будем, но выполним на чертеже.

Описанный в этой задаче метод построения сечения будем называть методом соответствия. Он позволяет найти пересечение секущей плоскости не только с одним ребром, а сразу с несколькими вертикальными рёбрами (или с их продолжениями).

З адача 3. Дано изображение пятиугольной призмы ABCDEA₁B₁C₁D₁E₁ и трёх точек M, N, P, которые лежат соответственно на ребрах EE₁, DD₁ и грани ABB₁A₁. Построить сечение призмы плоскостью, проходящей через M, N, P.

Решение. Мы будем искать пересечение секущей плоскости с рёбрами BB₁ и CC₁. Строим:

1. BEP₃D=Q₃, CEP₃D=R₃;

2. поднимаем Q₃, R₃ до PN и получаем точки Q и R;

3. MQBB₁=X, MRCC₁=Y;

4. XPAA₁=F, XYBC=G, NYDC=H;

5 . MNHGXF – искомое сечение.

Данный путь решения не является единственным. На следующем чертеже показано, как можно было найти пересечение секущей плоскости с ребром AA₁. Затем, используя линии FN и AD, мы можем найти пересечение с ребром CC₁. Сделайте это самостоятельно.

П ри построении сечений пирамиды все построения совершаются аналогично. Отличие лишь в том, что вторичные проекции точек строятся из вершины (а не с помощью вертикальных линий).

Задача 4. Дано изображение четырёхугольной пирамиды SABCD и трёх точек M, N, P, которые лежат соответственно на ребре SС и гранях SAB, SAD. Построить сечение пирамиды плоскостью, проходящей через M, N, P.

Решение. Строим сначала вторичные проекции данных точек: SPAD=P_o, SNAB=N_o. Вторичная проекция точки M уже есть – это C. В дальнейшем, это действие в построение мы включать

н е будем. Далее мы ищем пересечение секущей плоскости с ребром SA. Строим:

1. CAP_oN_o=Y_o;

2. SY_oPN=Y;

3. MYSA=X;

4. XPSD=F, XNSB=E;

5. XEMF – искомое сечение.