§11. Задачи на построение в аксонометрической проекции.

Следующие задачи мы будем использовать при построении сечений многогранников.

Задача 1. Прямая (a, a₃) лежит в плоскости заданной тремя точками (A, A₃), (B, B₃), (C, C₃), не лежащими на одной прямой. По заданной прямой a построить a₃.

Решение. Строим прямые AB, A₃B₃, AC, A₃C₃, BC, B₃C₃. Мы договорились, что направление проецирования не параллельно рассматриваемым прямым и плоскостям. Поэтому точки A, B, C не лежат на одной прямой

и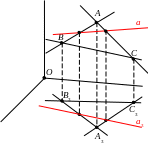 прямые AB, AC, BC не совпадают. Прямая a пересекает две из этих прямых в точках M и N. По этим точкам мы можем построить вторичные проекции M₃ и N₃ (для этого необходимо провести прямые параллельные OE₃). Тогда a₃=M₃N₃.

И наоборот, если задана прямая a₃, мы можем найти M₃ и N₃, по ним найти M и N. Тогда a=MN. Но здесь возможна ситуация, когда A₃, B₃, C₃ лежат на одной прямой. Тогда задача не имеет решения.

Задача 2. Точка (X, X₃) лежит в плоскости заданной тремя точками (A, A₃), (B, B₃), (C, C₃), не лежащими на одной прямой. По заданной точке X₃ построить X.

Решение. Точка (X, X₃) лежит в одной плоскости с точками (A, A₃), (B, B₃), (C, C₃). Поэтому прямые (XC, X₃C₃) и (AB, A₃B₃) лежат в одной плоскости. Пусть они пересекаются в точке (M, M₃) (если эти прямые не

п ересекаются, то пересекаются прямые (XA, X₃A₃) и (BC, B₃C₃), и мы рассмотрим их). Строим:

1. M₃=X₃C₃A₃B₃;

2. m||OE₃, M₃m;

3. ABm=M;

4. l||OE₃, X₃l;

5. lCD=X.

А налогично по точке X можем найти X₃. Самостоятельно разберите случай, когда A₃, B₃, C₃ лежат на одной прямой.

Задача 3. Построить следы прямой (AB, A₃B₃) на всех координатных плоскостях.

Решение. Очевидно, что X=ABA₃B₃ есть след прямой на O; ¯E1;¯E2;¯. Пусть (C, C₃) – точка пересечения прямой с O; ¯E1;¯E3;¯. Тогда C₃OE₃ и C₃A₃B₃  C₃A₃B₃OE₃. Для того, чтобы найти C проводим прямую, параллельную OE₃.

Аналогично строится след прямой на O; ¯E2;¯E3;¯.

Задача 4. Плоскость задана тремя точками (A, A₃), (B, B₃), (C, C₃), не лежащими на одной прямой. Построить её след.

Р ешение. Прямые (AB, A₃B₃) и (AC, A₃C₃) лежат на плоскости  их следы лежат на следе плоскости. Строим:

1. X=ABA₃B₃, Y=ACA₃C₃;

2. p=XY – след.

Если какая-либо из прямых не имеет следа, то вместо неё рассмотрим прямую (BC, B₃C₃).

Упражнение. Используя чертёж к задаче 1, постройте след плоскости.

З адача 4. Плоскость задана своим следом p и точкой (P, O). Точка (M, M₃) лежит на плоскости. Дана точка M. Построить M₃.

Решение. Точки (P, O) и (M, M₃) лежат на плоскости. Значит, прямая (PM, OM₃) тоже лежит на плоскости. Следовательно, её след X лежит на следе плоскости, причём, X=PMOM₃. Строим:

1 . X=PMp;

2. m||OE₃, Mm;

3. mOX=M₃.

Возможен случай, когда прямые PM и p не пересекаются. Это означает, что прямая P; ¯M; ¯ не имеет следа. Тогда она параллельна плоскости O; ¯E1;¯E2;¯. В этом случае OM₃||PM и мы можем её построить.

Упражнение. Разберитесь, как решается следующая задача. Даны след p плоскости и точка (M, M₃), принадлежащая плоскости. Найти точку (P, O) на оси O; ¯E3;¯.