§16. Смешанные фигуры.

К категории задач на смешанные фигуры относятся два типа задач. Первый тип: построить изображение одной пространственной фигуры, вписанной в другую. Второй тип: построить изображение общих точек двух пространственных фигур. Второй тип задач ещё называют позиционными задачами. К ним, в частности, относятся задачи на построение сечений.

З адача 1. Дано очертание сферы  и изображение её экватора – эллипс _o. Построить изображение правильной четырёхугольной призмы, вписанной в сферу, если её высота равна радиусу и параллельна линии, соединяющей полюсы.

Решение. Из условия задачи следует, что основания призмы в оригинале перпендикулярны отрезку N; ¯S; ¯ и делят отрезки O; ¯N; ¯ и O; ¯S; ¯ пополам. Поэтому основания призмы вписаны в окружности, которые получаются в сечении сферы плоскостями, параллельными экватору, и центры O1;¯ и O2;¯ этих окружностей – это середины отрезков O; ¯N; ¯ и O; ¯S; ¯. Такие сечения мы изображали в предыдущем параграфе.

П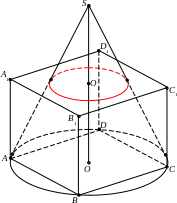 остроим изображение PQRT квадрата, вписанное в ₂ . Для того чтобы найти его вершины, требуется всего лишь провести два сопряжённых диаметра PR и QT эллипса ₂. С помощью параллельного переноса на вектор

O2O1;\s\up10( –( получаем изображение P₁Q₁R₁T₁ квадрата, вписанное в ₁. Остаётся провести изображения боковых рёбер призмы.

Задача 2. Даны изображения конуса и куба, причём основание куба вписано в основание конуса и высота куба в 2 раза меньше высоты конуса. Построить изображение общих точек конуса и куба.

Решение. Пусть S – изображение вершины конуса,  – эллипс, изображающий основание конуса. Оче­видно, пересечение конуса с верхним основанием куба есть окружность, подобная окружности основания конуса с коэффициентом 1/2. Изображение этого пересечения есть эллипс ₁ гомотетичный  с центром гомотетии S и коэффициентом 1/2.

Н айдём пересечение боковых поверхностей конуса и куба. Мы покажем, как построить точки пересечения с одной из боковых граней куба.

Выберем на ребре AB несколько точек N_i. Мы для примера выбрали три.Они служат проекциями на основание искомых точек M₁, M₂, M₃. Кроме того, искомые точки лежат на образующих конуса. Проекция образующей на основание есть радиус. Проводим через точки N₁, N₂, N₃ радиусы OP₁, OP₂, OP₃. Проводим через N₁, N₂, N₃ вертикальные линии l₁, l₂, l₃. Теперь M_i=OP_il_i. Напомним (это материал 1 семестра), что в пересечении получается гипербола.

У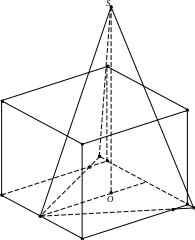 пражнения. 1. Даны изображения правильной треугольной пирамиды и куба (намеренно не все нужные линии сделаны штриховыми). Постройте линии пересечения боковых граней пирамиды с гранями куба.

2. Основание правильной треугольной пирамиды описано вокруг основания цилиндра, а высота пирамиды в 2 раза больше высоты цилиндра. Постройте изображения этих фигур и несколько точек пересечения боковых их поверхностей.

§16. Метрические задачи.

Пусть нам известно, что репер R ; ¯ = {O; ¯, E1;¯, E2;¯, E3;¯} является ортонормированным. Пусть на плоскости изображений  дано изображение R ={O, E₁, E₂, E₃} этого репера и даны две точки (M, M₃), (N, N₃). Тогда по чертежу мы можем определить координаты оригиналов M; ¯(x₁, y₁, z₁), N; ¯(x₂, y₂, z₂) и найти расстояние между ними о формуле

|M; ¯N; ¯ | = .

На самом деле, не обязательно требовать, чтобы репер R ; ¯ был ортонормированным. Достаточно знать длины отрезков |O; ¯E1;¯|, |O; ¯E2;¯|, |O; ¯E3;¯| и углы между ними. Тогда мы сможем составить матрицу Грамма =(g_ij) и вычислить расстояние между точками M; ¯ и N; ¯. Репер, матрица Грамма которого нам известна, будем называть евклидовым.

Для решения многих задач на построение достаточно знать, что репер определён своим изображением с точностью до подобия. Например, дано изображение куба. Тогда мы можем сказать, что R ={A, B, D, A₁} является изображением репера, подобного ортонормированному.

Определение. Изображение F фигуры F; ¯ называется евклидово определённым, если нему можно добавить изображение репера, подобного евклидовому, так что изображение станет полным (это касается как изображения пространственных фигур, так и плоских).

З адача 1. Дано изображение ABC прямоугольного треугольника A; ¯B; ¯C; ¯, у которого A; ¯=30, C; ¯ =90. Построить изображение высоты, проведённой из вершины прямого угла.

1 способ. Построить оригинал треугольника A; ¯B; ¯C; ¯ мы не можем, т.к. не знаем длины сторон, но мы можем построить A_oB_oC_o подобный оригиналу и в нём построить высоту C_oH_o. Искомая точка H делит AB в том же отношении, в каком H_o делит A_oB_o. Более того, мы можем построить A_oB_oC_o так, чтобы отрезки AB и A_oB_o совпадали. Тогда H_o совпадает с H.

2 способ. Мы можем вычислить, что H; ¯ делит A; ¯B; ¯ в отношении 3:1. Значит и H тоже делит AB в отношении 3:1.

Задача 2. Дано изображение ABCDA₁B₁C₁D₁ куба. Построить изображение перпендикуляра, проведённого из точки C; ¯ к диагонали A; ¯C; ¯₁.

Р ешение. Пусть в оригинале сторона куба равна a. Тогда мы можем вычислить, что |A; ¯C; ¯ |=a, |A; ¯C; ¯₁|=a. Мы строим треугольник ACC₁ подобный A; ¯C; ¯C; ¯₁, в нём проводим высоту CH. Искомая точка H делит AC₁ в том же отношении, в каком H делит AC₁.

Мы из точки проводим отрезок, равный C₁A (мы его так же и подписываем). Из точки проводим прямую, параллельную AA. В пересечении с C₁A получаем точку H. Переносим отрезок C₁H на основной чертёж. CH есть изображение перпендикуляра.

З адача 3. Дано изображение ABCA₁B₁C₁ правильной треугольной призмы у которой высота равна стороне основания. Построить изображение перпендикуляра, проведённого из точки A; ¯ к плоскости B; ¯C; ¯A; ¯₁.

Решение. Из соображений симметрии очевидно, что перпендикуляр должен падать на медиану A; ¯₁D; ¯ треугольника A; ¯₁B; ¯C; ¯. Значит, он лежит в плоскости треугольника A; ¯A; ¯₁D; ¯. Найдём его стороны, если каждое ребро призмы равно a.

| A; ¯D; ¯ |= a, |A; ¯₁D; ¯ |=== a.

Строим теперь AA₁D, подобный оригиналу A; ¯A; ¯₁D; ¯. В нём проводим высоту AE. Искомая точка E делит отрезок A₁D в том же отношении, в каком E делит отрезок A₁D.

47