§7. Изображение многогранников в параллельной проекции.

Теорема Польке-Шварца. Вершины произвольного четырёхугольника ABCD в плоскости изображений  могут служить изображением аффинного репера, равного данному реперу R ; ¯ = {A; ¯, B; ¯, C; ¯, D; ¯}.

Поясним формулировку. Для того, чтобы проекция данного репера на данную плоскость оказалась подобна ABCD, возможно понадобиться данный репер в пространстве повернуть. Тогда получится, что ABCD является изображением не данного репера, а равного ему.

Равносильная формулировка. Каков бы ни был четырёхугольник ABCD и аффинный репер R ; ¯ = {A; ¯, B; ¯, C; ¯, D; ¯}, существует такая плоскость , что проекция репера R ; ¯ на эту плоскость подобна ABCD.

Идея доказательства. Вершины репера можно рассматривать в качестве вершин тетраэдра (треугольной пирамиды). Пусть E – точка пересечения диагоналей в ABCD. Выберем на ребре A; ¯C; ¯ точку E1;¯, такую что

( A; ¯C; ¯,E1;¯)=(AC, E). Выберем на ребре B; ¯D; ¯ точку E2;¯, такую что (B; ¯D; ¯, E2;¯)= =(BD, E). Выберем теперь направление проецирования параллельно отрезку E1;¯E2;¯. Тогда точки E1;¯ и E2;¯ проецируются в одну точку E_o, и проекцией репера R ; ¯ будет четырёхугольник A_oB_oC_oD_o, аффинно-эквивалентный ABCD. Но нам нужно получить четырёхугольник не просто аффинно-эквивалентный, а подобный. Поэтому, возможно, понадобиться данный репер в пространстве повернуть. Таким образом,

полное доказательство значительно сложнее.

Р ассмотрим изображение некоторых многогранников. При этом мы предполагаем, что ни одна из граней многогранника не параллельна направлению проецирования. Тогда каждая из граней будет изображаться многоугольником, и изображение многогранника состоит из нескольких многоугольников.

1 . Из теоремы Польке-Шварца следует, что в качестве изображения вершин тетраэдра можно выбрать вершины любого четырёхугольника. Если для наглядности невидимые линии изобразить пунктиром, то получатся следующие возможные варианты.

2 . Каждая из граней параллелепипеда изображается параллелограммом. При этом, противоположные грани изображаются равными параллелограммами. Поэтому изображение параллелепипеда состоит из трёх пар параллелограммов, причём параллелограммы в каждой паре получаются друг из друга параллельным переносом.

Согласно теореме Польке-Шварца, мы можем в качестве изображения трёх вершин нижнего основания и одной вершины верхнего основания выбрать вершины произвольного четырёхугольника (например, ABDA).

З атем, изображения остальных вершин можно достроить однозначно.

3 . Изображение n-угольной призмы состоит из двух одинаковых n-угольников, которые получаются друг из друга параллельным переносом, и n параллелограммов. В качестве изображения трёх вершин нижнего основания и одной вершины верхнего основания мы можем выбрать вершины произвольного четырёхугольника (на чертеже мы эти точки выделили). После этого остальные вершины достраиваются однозначно.

4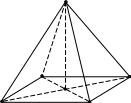 . Изображение n-угольной пирамиды состоит из многоугольника, изображающего основание и треугольников с общей вершиной, изображающих боковые грани. Согласно теореме Польке-Шварца, мы можем в качестве изображения трёх вершин нижнего основания и одной вершины верхнего основания выбрать любые 4 точки, из которых никакие три не лежат на одной прямой. Остальные вершины основания стоятся по правилам построения изображений плоских многоугольников (§5).

Если пирамида является правильной, то принято ещё изображать высоту, падающую в центр основания.