14 Распределение Максвела–Больцмана.

 Барометрическая формула для центрально-симметричного поля тяготения.  Найдем зависимость давления газа в атмосфере планеты от расстояния до центра в пространстве над поверхностью планеты

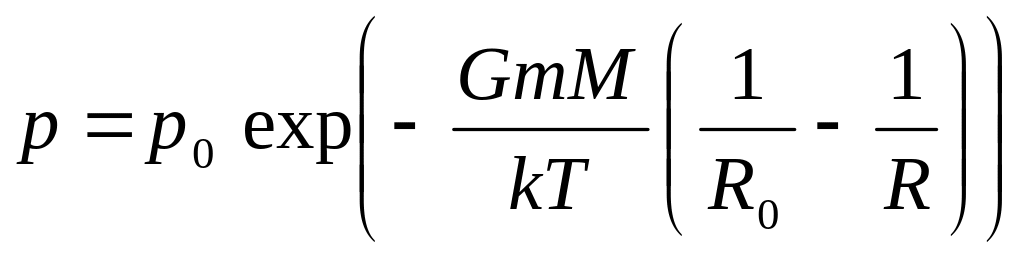
Барометрическая формула.  Здесь M – масса планеты, G – гравитационная постоянная, m – масса отдельной молекулы .Это барометрическая формула для центрально-симметричного поля тяготения для пространства R ≥ R₀.

Барометрическая формула для однородного поля тяготения.  У многих планет газовая оболочка очень тонкая.  У Земли, например, она не более 4-5% радиуса.  Поэтому при малых перепадах высот изменением напряженности поля тяготения можно пренебречь и считать его постоянным.  Формула в этом случае упрощается.

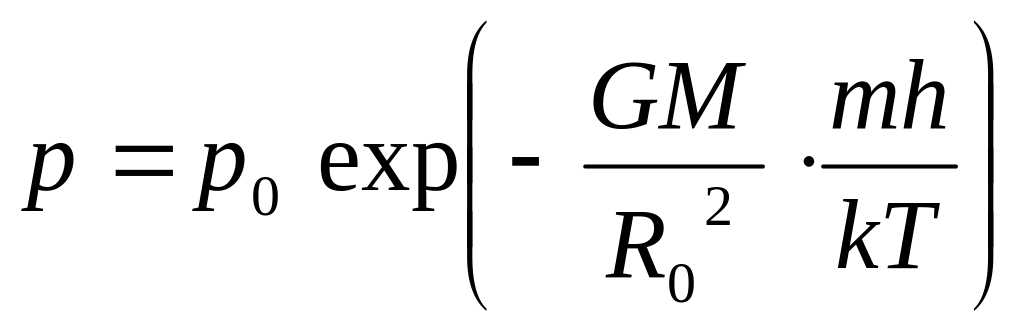Обозначим R = R₀ + h, где h<<R₀.  Тогда и . Здесь - ускорение силы тяжести на поверхности планеты. .

Барометрическая формула для однородного поля тяготения

Распределение Больцмана.  Если в барометрической формуле перейти от давления к концентрации по формуле Клаузиуса p = nkT, то получаем закон распределения молекул газа по высоте в однородном поле силы тяжести.

или или . В показатель экспоненты входит потенциальная энергия молекул в поле силы тяжести П = mgh.  Так что .  Распределение Больцмана, 1866.

Р аспред молекул или каких-то других частиц в потенциальном силовом поле в услов теплового равновесия по величине потенциальной энергии назыв распределением Больцмана.  Физическая природа силового поля роли не играет.  Важно лишь, чтобы поле было постоянно и консервативно.  Поэтому распред вида применимо и к другим объектам природы, например, к эл-м проводимости в металлах.

Функция распределения.  Благодаря тому, что молекулы реальн газов имеют конечный объем и потому часто сталк друг с другом, их скорости изменяются.  Но оказывается, что в любой момент времени распределение молекул по скоростям, как показывают теория и опыт, вполне опред и единственно возможное.

Задачу о распределении молекул по скоростям можно сформулировать так: какая часть молекул обладает скоростями, лежащими в некотором интервале вблизи заданной скорости.

Р ассмотрим газ в некотором объеме, в котором отсутствуют силовые поля.  Пусть n – концентрация молекул, то есть число молекул в единице объема, а dn/n – доля тех молекул, скорости которых лежат в интервале значений от u до u + du, где du – ширина интервала скоростей.  Очевидно, что чем шире интервал du, тем больше доля молекул, чьи скорости в нем заключены, dn/n ~ du.

Можно предположить, что коэффициент пропорциональности между этими величинами для разных скоростей разный и является функцией скорости u. Тогда соотношение переходит в равенство.  dn/n =f(u)du.

Ф ункцию f(u) называют функцией распределения.  Ее нашел теоретически Джеймс Максвелл в 1859 г.   . Функция распределения, Дж. Максвелл, 1859

Здесь B = m2kT, A = 4π(m2πkT)^3 2= 4π(Bπ)^3 2, где m – масса каждой молекулы, T – абсолютная температура газа, k – постоянная Больцмана.   Функция получена методами теории вероятностей на основе гипотезы о равновероятности всех направлений скоростей молекул.  

Максвелловское распределение молекул по скоростям является равновесным.  Каково бы ни было распределение в начальный момент времени, оно все равно в конечном счете перейдет в максвелловское f(u).  Это доказал Больцман в 1871 г.

U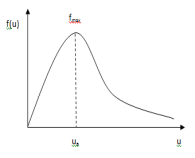 _{в -} это скорость, на которую приходится максимум функции распределения f(u).

Опыты Штерна.  Прямой проверочный эксперимент поставил впервые Отто Штерн в 1920 г.  с помощью атомных пучков.

Д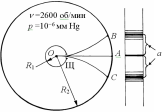 ва коаксиальных жестко связанных между собой цилиндра радиусами R₁ и R₂ вращались с угловой скоростью ω сначала в одну сторону, затем в другую.  Платиновая нить, покрытая серебром и натянут вдоль геометр оси цилиндров, нагревалась до температуры около 1300 K.  При этом серебро испарялось.  (T_пл серебра 1235 К).   Часть испар-ся атомов серебра, пройдя через щель Щ, формировали узкий пучок.  Скорость v движения атомов в этом пучке находилась так.

За время движения атомов между цилиндрами t = (R₂  R₁)/v цилиндры поворачиваются на угол =t = (R₂  R₁)/v.  Атомный осадок на внутренней стенке большого цилиндра смещается относительно центральной проекции щели (точка А) в точки B или C на расстояние a = R₂= R₂(R₂  R₁)/v.  Отсюда находится скорость движения атомов в пучке.

   . Штерн получил из опытов v  600 м/с для атомов серебра при температуре нити 1300 К.  Это качественно согласуется с распределением Максвелла.  Наиболее вероятная скорость для атомов серебра , среднеквадратичная скорость v_кв  550 м/с.  Если учесть, что расстояние a до центра пятна на внутр поверхности большого цилиндра находилось по визуальной плотности осадка, это неплохое соответствие теории эксперименту.

Сравнение осадка в точке A, полученного при покоящихся цилиндрах, с осадками в точках B и C показало, что если края полосы в точке A резко очерчены, а осадок в пределах полосы однородный, то края полос B и C размыты, плотность осадка убывает от середины к краям.  Это говорит о том, что скорости атомов в пучке разные.

Недостаток первых опытов Штерна состоял в том, что атомы серебра выходили не из газа, а с поверхности твердого тела.  Поэтому они несли информацию о распределении скоростей не в газе, а в твердом теле.