12. Основы мкт теории газов. Основное уравнение мкт. Статистическое истолкование температуры и давления. Уравнение менделеева-клапейрона. Изотермы реального и идеального газа.Уравнение вдв.

1.  Кинетическая модель идеального газа.  С точки зрения МКТ абсолютно идеальным является газ, представляющий собой сист из огромного числа м. т., то есть бесконечно малых частиц, не взаимод между собой и не сталкивающихся друг с другом.

При таких допущ частицы ид. Г. должны считаться совершенно свобод.  Это значит, что движутся они прямолинейно и равном от одного соуд со стенкой сосуда до другого.  Каждая частица ид. Г. ведет себя так, как будто других частиц вокруг нее нет.

Физические законы и следствия, которым ид. газы подчиняются точно, справедливы с опред погрешностью и для реальных газов.

2.  Основное уравнение кинетической теории газов.  Поскольку газ есть система из хаотически движущихся с разными скоростями молекул, то можно предположить, что давление газа на стенки сосуда есть результат множества соударений молекулы со стенками.  Поэтому должна быть определенная количественная связь между средними параметрами движения молекул и величиной давления.

Скорости молекул газа различны по величине.  В действительности скорости молекул газов разные не только по направлению, но и по величине.

Предположим, что газ состоит из нескольких групп молекул.  Массы всех молекул одинаковы и равны m, а скорости молекул одинаковы по величине лишь в пределах групп.  Пусть в группе 1 – скорости молекул , в группе 2 – скорости молекул ,… в группе i скорости молекул .

Парциальное давление газа каждой группы определится также формулой : , где - концентрация молекул газа в i-той группе.

По закону Дальтона для парциальных давлений суммарное давление газа в целом есть сумма парциальных давлений, _.

Сумму можно представить так: , где n – концентрация всех молекул газа, а - средний квадрат проекции скорости всех молекул.

Заметим, что число групп молекул в единице объема может достигать .  То есть каждая молекула может иметь отличную от других молекул скорость, так что число групп будет равно числу молекул. Итак,

здесь входит средний квадрат проекции скорости.

Перейдем от проекции скорости к модулю скорости u. Вектор скорости любой молекулы можно представить как сумму составляющих по осям.   ,

или .

Направления скоростей равновероятны.  Поэтому средние квадраты для системы с большим числом частиц одинаковы, .  Тогда , .

Подставляем.   .

Основное уравнение кинетической теории газов

Давление в газах пропорционально концентрации молекул n и их средней кинетической энергии хаотического поступательного движения.

Температура T и давление p - статистические величины. Эти понятия применимы лишь к системам с огромным числом молекул, соизмеримым с числом Авогадро N_A = 6,02210²³ моль^1

Св-ва газа как системы частиц не сводимы к свойствам отдельных молекул.  Такая система проявляет новые качества и хар-ся новыми физическими величинами – давлением p и температурой T.  Здесь проявляется диалектический закон перехода количества в качество.  Свойства газов определяются усредненными параметрами молекул – средней кинетической энергией , средней скоростью , средним импульсом .  Средние величины находятся методами статистики.  Раздел физики, методом исследования в котором является статистика, называется статистической физикой.

Основное уравн МКТ для ид.г. уст связь м/д макропараметромпараметром Р и микропарам-ми , но для решения практич задач важно знать связь м/д макропараметрами Р,V,T,m. Уравнение Менделеева-Клапейрона. , где R=N_ak=8,31Дж/мольК-унирерсальая газовая постоянная.

k = 1,3810^23 Дж/К.

Газ холод-ый и плотный не будет подчин-ся уравнению Мен-Клап. РГ подчин-ся Ур-ию Ван-дер-Ваальса. , а для одного моля в-ва . Здесь b- поправка на собст-ый объем мол-л где N- число всех м-кул. Поправка а учитывает взаим-ие притяжения (зависит от газа). Притяжение м/у мол-ми приводит к тому, что поверх-ый слой стяг-ся внутрь, создает добавочное давление. Уравнение В-Д-В хорошо работает для достаточно нагретого и не очень плотного газа. Но для хол-го и плотного его точность плохая. тем не менее на кач-ом уровне оно работает и в этой обл-ти и даже до некот-ой степени опис-т пер-од Ж-Г и обратно. Наглядно РГ и ИГ м/о показать на изотерме этих газов.

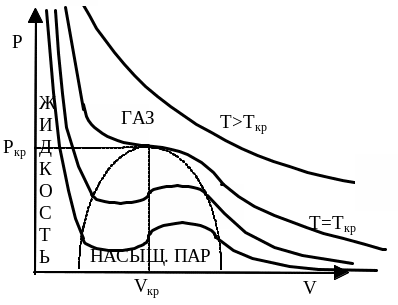
Штриховая кривая разделяет три фазы. При Т>T_кр изотерма мало отл-ся от гиперболы. По мене понижения темпер-ры изотерма пара стан-ся все более похожей на куб-ую параболу. Если изотермически сжимать ненесыщ-ый пар при Т<Т_кр, то конц-ия молекул возрастет и соотв-но, давление будет возрастать вплоть до давления насыщ-го пара. При дальн-ем уменьшении объема на дне сосуда образ-ся жидкость и устан-ся динам-ое равновесие м/у нас-ым паром и жидкостью. Давление нас-го пара ост-ся неизменным, а с уменьшением объема все большая часть пара перех-т в жидкость. Гориз-ый участок на изотерме обусловлен процессом превр-ия части пара в жидкость. Ур-ие М-Кл с дост-ой степенью точности выполн-ся, но надо помнить, что масса пара не ост-ся при сжатии пост-ой. Процесс умен-ия объема при дальн-ем сжатии прекр-ся, когда весь газ в сосуде превр-ся в жидкость. Резкое возр-ие давления при дальнейшем уменьшении объема объясн-ся малой сжим-стью жидкости.