28.Перем. Эл. Ток

Получение гармонич. тока технич. частоты. Перем наз-ся ток электр зарядов, величина и направление к-го изменяются во времени. З-н измен-я тока м. б. каким угодно. Но в практике наиболее важны гармонич. токи, их величина измен-ся во времени по з-ну sin или cosin. Если частота изменений тока не превышает нескольких сотен герц, её называют технической (промышленной). Перем. токи промыш. частоты исп-ются в кач-ве носителей энергии. Если S – пл-дь контура, а n - его единичная нормаль, то маг. поток, прониз-щий контур, есть _{Если контур}

покоится, то Ф=const, и ЭДС инд-ии в контуре нет. При вращении жёсткого контура (S = const) в однород. маг. поле (B=const) в нём наводится ЭДС индукции

технически удобнее реализовать равномер. вращ-е контура, когда =t, где угл. скорость вращения. Отсюда ddt= и ε=BSsin=ε_asint (3) Здесь ε_a = BS  амплитуда ЭДС. (4) Если контур замкнут на некот. сопр-ние R, то под действием переем. ЭДС в контуре возникает переем. ток той же частоты, колебания кот. совпадают по фазе с колебаниями ЭДС

_{З десь}  амплитудный ток.

Частота колебаний тока  =  / 2,, период Т = 1 = 2.

Цепь с актив. сопр-ем R, L=0 и С=0. Пусть в цепи действует внеш. синусоид. ЭДС  = _а Sint В случае квазистац. тока в люб. мом-т времени дл

_{контура справ-во 2-е пр-ло Кирхгофа} i R = _a Sint, .

Ток ч/з актив R совпадает по фазе с ЭДС. Т. к. напряжение на сопр-нии равно ЭДС, то мож. сказать, что измен тока и напряжения на актив. R совпад по фазе.

Цепь с конд-ром,(С-емкость) 2-е пр-ло Кирхгофа запишется так: i R + u_c = .. Но R = 0, u_c =  (u_C – напряжение на обкладках конд-ра. Т. к. u_C = qC, где q – заряд на обкладках конд-ра, то ^{получаем:} , или q = _a CSint

^{Продиф-вав по времени получаем ток в цепи}

с ёмкостью

_{Выражение есть амплитудный ток.}

1С = X_C - сопр-ние конд-ра переем. току – ёмкостное сопр-ние. Т. к. cost = sin(t + 2), то, сравнив напряж-е на конд-ре u_c =  = _a Sint t с током i = i_asin(t + 2), видим, что ток в цепи опережает напряж-е на конд-ре на 1/4 периода Если сместить начало координат на 2 влево, для чего из аргументов ф-ции вычесть 2, то выраж-я для тока и напряж-я приним. вид:

Цепь с катушкой, R=0,. В контуре дейст-ют две ЭДС: внеш. гармонич.  = _a Sint и ЭДС индукции, противодейст-щая направлению изм-ния внеш.. По 2-му пр-лу Кирхгофа их сумма в люб. мом-т времени=0 т к R=0

Чтобы выразить зависи i(t), разделяем переменные и интегрируем

^{Пост. интегрир-ния i}₀

отбрас-ем, т. к. это составляющая пост. тока ч/з катушку и в данном исслед-нии не интересна.^,

Sin(t - /2) = i_a Sin(t - /2). Величина L = X_L им. смысл индуктив. сопр-ния цепи. Напряж-е на зажимах катушки совп-ет с внеш. ЭДС. u_L = _a Sint = u_La Sint Поэт. ток в цепи с L отстаёт от напряж-я на L сопр-нии на 1/4 периода. Если сместить на графике начало корд-т на 2, то выражения для тока и напряж-я на индукт-ти приним-т вид:

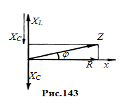
З-н Ома в цепи переем. тока. Рассм. цепь, включающую в себя R, C и L. Если ток квазистац-ый, то в люб. мом-т времени его величина одинакова во всех точках цепи и равна i = i_acost. U на каж. эл-те цепи соотв-но равно u_R = i_aRcost, u_C = i_aX_Ccos(t  2), u_L = i_aX_Lcos(t + 2). Как пр-ло, диаг-мы изобр-ся в тот мом-т времени, когда i = i_a). Каж. вектор амплитуд. напряж-я м представить как произведение действит-го числа i_a на векторы R, X_C, X_L, Поэтому для вычисления полного сопр-ния цепи нужно найти векторную сумму сопр-ний всех эл-тов цепи, соединённых послед-но. Модуль полного сопр-ния Z равен

|X_L  X_C| - реактив. сопр-ние. Умножив диагр-му сопр-ний на скаляр. величину амплитуд. тока i_a, получаем диагр-му напряж-ий .Угол  определяет сдвиг по фазе м/у I в цепи i и прилож. к ней U u. М/у величинами амплитуд. тока i_a и амплитуд. напряж-я u_a сущ-ет пост. связь. _{Разделив это выр-ние на , получаем Но }

эфф. ток. Если ввести по формальной аналогии

^{понятие эффект. напряж-я ,то}

^{получаем: З-н Ома для цепи}

переем. тока. Эфф I протекающий по участку цепи, пропорц. эфф. U, приложенному к этому участку, и обратно пропорц. полному R цепи.

Дейст. и ср. значение перем. тока. для хар-ки перем. тока во мн. случаях удобнее указывать величину пост. тока, производящего такое же действие, как и данный переем-ый. В кач-ве такого действия принято брать тепловой эффект. соотношение м-у эффект. (действующим) и амплит. токами. За один период Т перем. Ток

^{выделяет тепло}

Но такое же кол-во тепла за время Т выд-т пост. ток некот. величины I. Так что

_

_{Подставив сюда i = iasint  получаем -} эфф. знач-е тока . Пост. ток i_ср переносит за 1/2 периода такой же заряд q, как и данный переем _Отсюда

Матем-ски эфф ток есть среднекв-ный, а ср. ток–среднеариф-ий по модулю. Выразив из получ-х ф-л амплит. ток i_a, найдём связь м/у эфф. и ср. токами.

^

Квазистационарные токи – это такие перем токи, при к-х мгновенные значения I практически одинаковы во всех точках цепи. Т.к. распространение элек и магн полей в пространстве происходит с конечной скоростью, то для того, чтобы в самых отдалённых участках цепи “почувствовалось” изменение ЭДС, д пройти некоторое время . Если ЭДС изменяется очень быстро, то напряжённость электр поля в удалённых точках цепи не успевает за изменением ЭДС.

Если l – линейный размер контура, с – скорость распространения в контуре эм волны, то  = lc. Время полного изменения ЭДС равно периоду Т. Если период Т много больше времени , то ток является квазистационарным.

Т >> lc, или Tc >> l, или длина цепи l << λ длины эм волны, соответствующей переменному току. Критическое значение частоты  в цепи _max = сl. Выражения формул через синус и косинус. Часто I и U удобно выражать ч.з ф-ю cos. Фазовый сдвиг м/у I и U на элементах цепи остаётся прежним, а сам переход от ф-и синуса к ф-и косинуса графически соответствует переносу начала координат по оси аргументов на 2 вправо.

Здесь X_L =  L, X_C = 1С.

Мощность в цепи переменного тока. Мгновенное значение мощности в цепи переменного тока есть p = iu , где i и u – мгновенные I и U

Пусть между I и U есть сдвиг по фазе на угол .

Среднее значение мощности переменного тока за период T найдётся интегрированием. . Т.к. cos(t + ) = cost cos  sint sin, а cos²t = (1+cos2t)2 .

Cos и sin - const данной цепи числа и выносятся из под интеграла. Правый интеграл обращается в нуль, а левый от cos²t распадается на два .

Здесь I и U – эффективные ток и напряжение.

Величина cos называется коэффициентом мощности. Чем > косинус фи, тем < бесполезные потери в цепи переменного тока.

определяет активную мощность, к-я х-ет скорость необратимого превращения электр энергии в другие виды энергии.

Произведения эффективных I и U н-ют полной мощностью и обозначают S.

IU = S, P = Scos.

Q  = IUsin = Ssin - реактивная мощность. Она х-ет скорость передачи энергии от источника тока к приёмнику и обратно.

Величины P, S, Q образуют в комплексной плоскости треугольник мощностей для цепи с преобладанием индуктивности.

Ед активной мощности P – ватт (Вт), ед полной мощности S – вольт-ампер (ВА), ед реактивной мощности Q – вольт-ампер-реактивный (вар).

Реактивная мощность, потребляемая в электрических цепях, вызывает дополн активные потери в подводящих проводах. Для устранения перегрузок и повышения коэффициента мощности делают компенсацию реактивных нагрузок, максимально приближая X_L  к X_C. Амперметры и вольтметры в цепях переменного тока проградуированы на эффективные I и U. Поэтому произведение показаний амперметра и вольтметра, подключённых к нагрузке, даёт полную мощность S, потребляемую данной нагрузкой. Для измерения активной мощности применяются специально сконструированные ваттметры

29. Эл. колебания в колеб. контуре.

К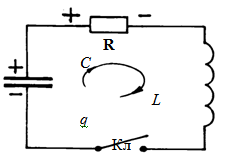 олеб. контур - цепь, содержащая С и L. Реальный контур всегда имеет некот.активн (омическое) R.

Свобод. (незатух.) колебания в контуре В идеал. контуре, в кот. отсутствует затухание, R = 0, колебания должны продолжаться бесконечно долго. При этом макс. энергия конд-ра , а макс. энергия поля катушки составляет . Когда конд-р макс-но заряжен, i = 0, , вся энергия колебаний заключена в эл. поле. Когда конд-р разряжен, u = 0, а ток максимален вся энергия контура заключена в маг. поле катушки. Ср. и макс. энергии эл. и маг. полей одинаковы, . Однако колебания в люб. реал. контуре даже из сверхпроводящих материалов обязательно затухают. Это происходит потому, что контур с перем. током излучает электромаг. волны, кот. уносят запасённую в нём энергию. В дифф-ном ур-нии эти потери не учтены.

- ф-ла Томсона.

декремент затухания

- логарифм-ий декремент затухания

- волновое сопр-ние

Затух. колебания Если на пластинах конденсатора есть заряд q, то при замыкании ключа в цепи возникает изменяющийся во времени ток. Для его определения составим дифф. ур-ние, описывающее изменение заряда на обкладках конд-ра. В случае квазистац. тока для контура справедливо 2-ое пр-ло Кирхгофа: iR=UC+. Здесь i=dq/dt, , Отсюда: ,или Это дифф. ур-ние затух. колебаний. Его решение зависит от соотношения между коэф-тами. Обозначив R/L=2n, 1/CL=₀², получаем

а). Периодич. затух. колебания. Если >>n, то решение имеет вид:

q = q₀ e-nt cost,

i = q₀  e-ntcos(t + /2),

.Здесь

б ). При n>w разряд конд-ра апериодический, а w и Т мнимые числа. Если n>>w, заряд на конд-ре при разряде и заряде изменяется по экспоненц. з-ну. При разряде: . При зарядке: . Здесь

Из равенства n=w0 находим критическое сопр-ние контура. При R<<Rкрит в контуре возникают периодические колебания, при R>Rкрит-апериодические.

2).Вынужденные колебания. Если в контуре действует периодич. ЭДС аcost, то уравнение колеб. электр. заряда на обкладках конденсатора принимает вид: Решение этого ур-ния состоит из 2-х членов, и при n<<w0 имеет вид:

.

Первый член описывает собст. затух. колебания в контуре. Спустя время t>>(-время релаксации колеб.) эти колебания практически исчезают. Остается лишь 2-я часть описывающая вынужденные колебания: q|t>>=Bcos(t-), В- амплитуда вынужд. колебаний. ; ; Дифф-я по времени, получаем ток в контуре. i = = - BSin(t - ) = BCos(t -  + /2). Величина В= iа есть амплитудный ток. Он зависит от соотношения частот 0 и .

Если частота изменения внеш. ЭДС  приближается к собст. частоте своб. колебаний в контуре 0, то ток возрастает до некоторого макс. значения, называемого резонансным. При 0 последняя формула примет вид:

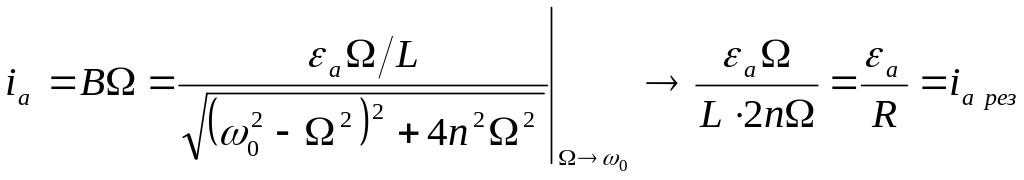
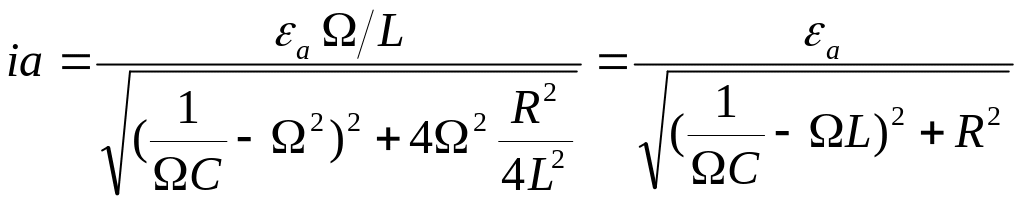Очевидно, резонансная частота , а резонансный ток iа=а/R. Рассмотренная ситуация соответствует резонансу напряжений (последов. резонансу) в цепи переем. тока, а ф-ла амплитуд. тока соответствует з-ну Ома для цепи переем. тока. Т.к. , n=R/2L, то Чем больше добротность контура, тем уже его резонансная кривая, тем выше его избирательность (селективность). Поэтому с увеличением добротности Q ширина частот 0, при которых в контуре раскачиваются значительные токи, становятся уже. Этот интервал частот, близких к 0, называется полосой пропускания контура.

Искровой колебательный контур.

Для возбуждения в колебательном контуре незатух. колебаний выс. частоты использ-ся Искровой колебательный контур, которой изобрёл в Герц. После включения ист-ка пост. напряжения конд-р ч/з дроссельные катушки заряжается, и напряжение м/у его обкладками увелич-ся. Когда оно достигает значения напряжения пробоя, через разрядник проскакивает искра, замыкающая колеб. контур, и в контуре возникает цуг затух-х колебаний. Он обрывается, когда напряжение на искровом разряднике упадёт до напряжения гашения искры.

Искровой колебательный контур представляет собой автоколебательную систему. Один из главных недостатков его в том, что энергия вводится слишком редко– м/у цугами. Поэтому трудно обеспечить стабильность амплитуды ВЧ колебаний

Генератор ВЧ колебаний на ламп. триоде.

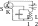
Вследствие тепловых флуктуаций электронов контуре C–L1 самопроизв возникают слабые колебания. Но изменение напряжения на обкладках конденсатора С вызывает изменение потенциала сетки S триода. При полож-ном потенциале верхней пластины конд-ра триод открывается, в анодной цепи течёт ток, кот. ч/з индуктивную связь м/у катушками L1 и L2 усиливает ток в контуре. Когда конд-р перезарядится в обратном направлении, лампа заперта, ч/з катушку L2 тока нет. Затем весь процесс повторяется. Т. о., ток в анодной цепи течёт лишь в те мом-ты времени, когда лампа открыта, и когда маг. поле катушки L2 подпитывает ток в контуре. Управление электронной лампой с помощью цепи обратной связи может осущ-ся разными способами. Наряду с рассмотренной индуктивной связью часто применяется также ёмкостная и автотрансформаторная обратная связь.

Токи высокой частоты, ТВЧ. С помощью генераторов эл. колебаний можно вырабатывать почти синусоидальные перем. токи частотой в тысячи и миллионы герц. Благодаря вытеснению быстроперем. токов к периферии пр-ка вследствие скин-эффекта, оказывается возможным с помощью ТВЧ закаливать поверхность стальных деталей, не уменьшая их пластичности в глубине. Использ токов частотой в сотни и тысячи герц эффективно при индукционном нагреве металлов в плавильных индукционных электропечах, поскольку вихревые токи Фуко увеличиваются с ростом частоты электромаг. поля.

ТВЧ широко используются при высокочастотной сварке и в многоканальной телефонной связи.