27. Уравнения Максвелла.

Гипотеза Максвелла о вихревом электрическом поле. Анализируя явление электромагнитной индукции, Максвелл сделал в 60-х. предположение, что причина появления ЭДС индукции состоит в возникновении электрического поля. Это электрическое поле создаётся изменяющимся магнитным полем. При этом проводники играют второстепенную роль. Они являются своеобразными приборами, обнаруживающими это поле. Под действием поля заряды проводимости в проводнике приходят в движение, и если проводник замкнут, в нём возникает индукционный ток.

Электрическое поле, возникающее при электромагнитной индукции, является вихревым. Его силовые линии замкнуты. ЭДС индукции есть , где Ф – поток магнитной индукции B через площадку S, ограниченную рассматриваемым контуром. В общем случае Здесь Bn  проекция вектора магнитной индукции B на нормаль n к контуру. С другой стороны, действующая в любом контуре ЭДС может быть представлена как циркуляция вектора электрической напряжённости сторонних сил.

Здесь Ест - напряжённость вихревого эл п, Е_l – проекция вектора Ест на касательную к контуру.

Приравняв правые части выражений, получаем количественную связь между напряжённостью вихревого электрического поля и скоростью изменения потока.

.Это ур-е обобщает з-н эл.м. индукции Фарадея. В системе уравнений Максвелла в интегральной форме его обычно записывают вторым.

2. Токи смещения. Гипотеза Максвелла о возникновении вихревого электрического поля, из соображений симметрии, приводит к обратному заключению: всякое изменение электрического поля должно вызывать появление вихревого магнитного поля.

Если включить конденсатор С в цепь, то пока он заряжается, в цепи через лампочку Л будет проходить электрический ток. При изменении переключателем Пк полярности включения конденсатора ток через конденсатор потечёт в обратном направлении до полной перезарядки. Если после каждой перезарядки переключателем Пк менять полярность включения конденсатора, можно заставить лампочку светиться практически непрерывно. Через лампочку течёт пульсирующий ток одного направления, а через конденсатор – ток переменного направления.

Итак, в отличие от постоянных переменные токи могут существовать и в разомкнутых цепях (в конденсаторе разрыв цепи). В проводниках при этом движутся заряды проводимости, а в пространстве между пластинами конденсатора существует лишь переменное эл. п. Поскольку в этом поле происходит переменная поляризация диэлектрика, то есть переменное смещение связанных зарядов диэлектрика, Максвелл назвал его током смещения. Можно сказать, что ток проводимости в проводнике замыкается током смещения в диэлектрике.

1 уравнение Максвелла в интегральной форме.Согласно Максвеллу, переменное эл. п. в конденсаторе в любой момент времени создаёт такое же м. п., как если бы между обкладками существовал ток проводимости, равный току в проводниках. Иначе, м. п. разомкнутого контура такое же, как если бы контур был замкнут. Это предположение позволяет установить количественную связь между изменяющимся эл.п. и генерируемым им м. п..

Ток в проводнике можно определить как скорость изменения заряда на обкладках конденсатора где σ – поверхностная плотность зарядов на обкладках площадью S. Разделив на S, получаем плотность тока . Если плотность зарядов σ выразить через напряжённость эл. п. в конденсаторе из формулы , σ = εε0Е, и сохранить векторный характер величин j и Е, то получаем плотность тока смещения .Переменное во времени эл. п. создаёт такое же магнитное поле, как и ток проводимости плотностью .

В любой т проводника может существовать как ток проводимости, так и ток смещения. Поэтому плотность полного тока j равна их сумме. .Здесь N – поток вектора электрической напряжённости через площадку S. Интеграл от плотности тока проводимости даёт ток проводимости i через площадку S: .

После подстановки получаем первое уравнение Максвелла . Это ур-е обобщает з-ны Ампера и Био-Савара-Лапласа.

Опыты Роуланда и Эйхенвальда. То, что м. п. возникает вокруг проводника с током ещё не означает, что поле создаётся движущимися эл. зарядами. Не исключалось, что м. п. создаёт проводник, переходящий в некое новое качество, когда в нём существует эл.ток. Поэтому было важно на опыте доказать, что м. п. создаётся любыми эл. зарядами, движущимися в любой среде. Тем самым м. п. токов смещения из гипотезы превращалась бы в реальный факт.

В 1878 г. в лаборатории Гельмгольца американец Генри Роуланд с целью проверки гипотезы Максвелла поставил следующий опыт. Эбонитовый диск толщиной 0,5 см и диаметром 21 см имел на верхней поверхности кольцеобразный носитель электричества – разрезанное в точках а и в кольцо из золочёной фольги. Диск устанавливался на оси и помещался в заземлённую металлическую коробку. Коробка и кольцевой носитель представляли собой конденсатор, ёмкость которого было нетрудно вычислить или измерить. Если к носителю приложить относительно коробки напряжение U, то, зная ёмкость системы, можно всегда определить заряд q на носителе.Над коробкой помещался магнетоскоп М – подвешенная на тонкой нити маленькая магнитная стрелка с зеркальцем, ориентированная в состоянии покоя касательно диску. Когда диск вращался с частотой около ν = 60 об/с, движущийся с кольцевым носителем заряд создавал круговой ток. В результате магнитная стрелка отклонялась, что говорило о появлении м п. Количественная проверка состояла в следующем. Диск останавливался, к точкам а и в носителя подключались проводники, и через кольцевой носитель пропускался такой ток проводимости, при котором магнитная стрелка отклонялась на ту же величину.

Сравнение конвективного тока i = q ν, обусловленного вращением носителя, с током проводимости показало, что токи совпадают.

Опыты Роуланда повторялись с разными результатами и другими исследователями, пока в 1901 – 1904 г.г. русский физик Александр Эйхенвальд окончательно не доказал, что все наблюдаемые в экспериментах токи – проводимости, конвективные и токи смещения – всегда образуют собой замкнутые цепи и генерируют магнитные поля.

Система ур-й Максвелла в интегральной форме. Всё содержание теории электромагнетизма может быть сконцентрировано в группе математических соотношений, полученных Максвеллом в 60-х годах XIX в. на основе обобщения эмпирических законов электрических и магнитных явлений.

Полная система у-й, описывающих поля и заряды, включает в себя кроме уравнений поля выражения для сил, действующих на заряды, и законы динамики Ньютона, описывающие движение носителей зарядов под действием этих сил.

Взаимод полей с материальными средами описывается с помощью макроскопических параметров ε, μ, g, значения которых могут быть в первом приближении вычислены в рамках моделей микроскопической электродинамики. Электромагн явления в области атомных размеров и внутри самих атомов и молекул могут быть описаны только с помощью квантовой электродинамики.

Уравнения М. для с-мы зарядов в вакууме:

Первая и вторая пара ур-й М. в дифференц-ой форме:

Первая и вторая пара ур-й М. в интегр-ой форме:

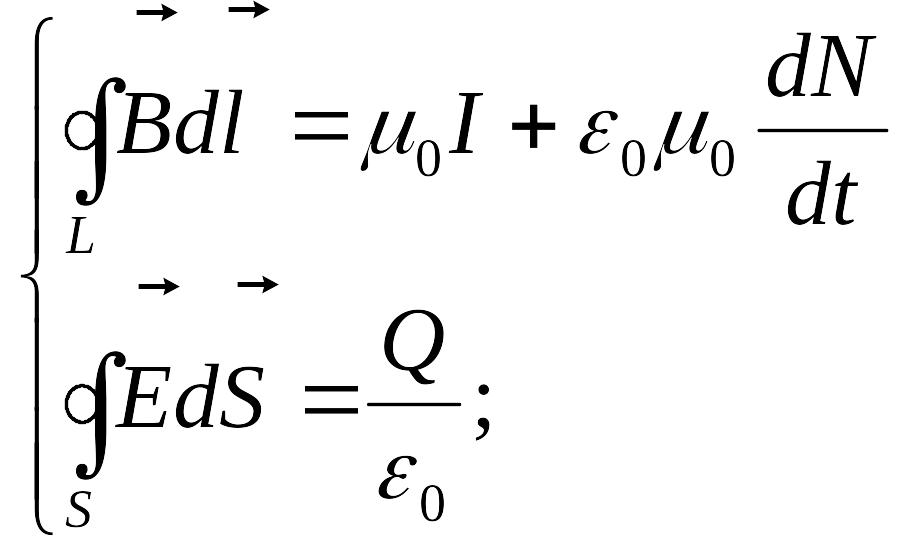
Q - пространственный заряд. Эти уравнения выражают связь между напряженностью м. п. и эл. п. Полная система ур-й, описывающих поля и заряды, включает в себя кроме уравнений поля выражения для сил, действующих на заряды, и законы динамики Ньютона, описывающие движение носителей зарядов под действием этих сил.

Из 1-го (эм индукция) и 3-го (з-н полного тока (закон Ампера)) диф-х ур-й видна взаимосвязь м-у полями (асимметрия-наличие э.м. волн, т.к. знаки разные), двусторонняя связь полей одно из к-рых с «-» дает возможность сущ-ния эл.м. волн.

2-з-н отсутствия магнитных зарядов в природе, 4- з-н Кулона в форме теоремы Гаусса.

В целом, решение этих уравнений довольно затруднительно, так как они зависят еще и от координат, и от времени.

Эл.м. волна представляет собой эл.м. возмущение, распространяющееся в вакууме со скоростью света.

С лучай плоской волны более простой - это волна , в которой векторы Е и В зависят лишь от времени и одной координаты. 1). ;2). ; где -единичный вектор, задающий направление движения фронта волны. Часто используются уравнения волны вида: ; , где ; ; или w=2pn - циклическая частота; k=2p/l - волновой вектор. Скорость распространения волны есть величина: , где с - скорость света. Максвелл сделал вывод, что свет и эм волны имеют одну природу, свет-это частный случай эм волны. В однородном диэлектрике -это закон Максвелла. Максвелл ввел особую - полевую форму материи, которая не может существовать в покое и движется со скоростью с. Плоская волна может быть линейно поляризованной, т.е. плоскость колебаний векторов Е и В неизменна во времени. Световое поле - это усреднение квантовой картины взаимодействия фотонов и связанных в атомах электронов.

Условия излучения эл.м. волн. Важное практическое значение имеют электронейтральные системы, излучающие электромагнитные волны; системы характеризуются электрическим дипольным моментом и магнитным

дипольным моментом .

Выделяют два вида излучения:

1 .Электр дипольное излучение , возникает, если р¹0 ;

2.Магнитное дипольное излучение, чья интенсивность на несколько порядков меньше электрического дипольного излучения (возникает, если ¹ 0).

Шкала эл.м. волн: радиоволны - 10⁵-10¹² м, инфракрасные - 810^-7-10^-9 м,видимыйсвет-(ф)4*10^-7-(к)8*10^-7м, ультрафиолетовый-1*10^-8-4*10^-7м, рентгеновские лучи - 10^-14-10^-8 м (проходят через вещество), гамма-излучение-l 10^-10м (корпускулярные свойства).

Энергия и импульс э/м поля.

Перенос энергии и импульса в ЭМ-волне. Эл.м.волны переносят в пространстве энергию.

В случае упругих волн эта энергия слагается из потенциальной энергии деформации среды и кинетической энергии движения её частиц. Энергия же электромагнитных волн слагается в любой момент времени из энергии взаимосвязанных электрического и магнитного полей.

Э нергия, переносимая электромагнитными волнами определяется вектором плотности потока энергии S, то есть количеством энергии, которое переносится волновым процессом через единичную площадку σ, ориентированную перпендикулярно вектору скорости движения волнового фронта v в данный момент времени . Здесь w₀ – плотность энергии ЭМ-поля. Так как ;

Вектор S можно представить через характеристики ЭМ-поля E и B. Как и в колебательном контуре средние энергии электрического и магнитного полей в ЭМ-волне одинаковы. Е и В изменяются в одной фазе, то одинаковы и мгновенные значения плотности энергии, то есть εε₀E² = B²μμ₀ в итоге можно записать: .Вектор Пойнтинга

Э лектромагнитное поле массой и импульсом. Из формулы Эйнштейна W = mc² = w₀V, где V – объём, получаем пространственную плотность распределения массы поля:  .

Импульс единичного объёма электромагнитной волны есть .

Пон-е эн-гии в физике соот-ся с пон-ем работы (эн. рассм-ся как запасы работы, кот. м.б. совер-на).

-

энергия э/м поля в заданном объеме.

-импульс э/м поля.

-объемная плотность энергии поля.