
Векторная форма
В дифференциальной форме закон Фарадея можно записать в следующем виде:
![]() (в
системе СИ)
(в
системе СИ)
или
![]() (в
системе СГС).
(в
системе СГС).
В интегральной форме (эквивалентной):
![]() (CИ)
(CИ)
или
![]() (CГС)
(CГС)
Здесь
![]() —
напряжённость
электрического поля,
—
напряжённость
электрического поля,
![]() —
магнитная
индукция,
—
произвольная поверхность,
—
магнитная
индукция,
—
произвольная поверхность,
![]() —
её граница. Контур интегрирования
подразумевается
фиксированным (неподвижным).
—
её граница. Контур интегрирования
подразумевается
фиксированным (неподвижным).
Токи Фуко (в честь Фуко, Жан Бернар Леон) — это вихревые замкнутые электрические токи в массивном проводнике, которые возникают при изменении пронизывающего его магнитного потока. Вихревые токи являются индукционными токами и образуются в проводящем теле либо вследствие изменения во времени магнитного поля, в котором находится тело, либо вследствие движения тела в магнитном поле, приводящего к изменению магнитного потока через тело или какую-либо его часть. Величина токов Фуко тем больше, чем быстрее меняется магнитный поток.
В отличие от электрического тока в проводах, текущего по точно определённым путям, Вихревые токи замыкаются непосредственно в проводящей массе, образуя вихреобразные контуры. Эти контуры тока взаимодействуют с породившим их магнитным потоком. Согласно правилу Ленца, магнитное поле вихревых токов направлено так, чтобы противодействовать изменению магнитного потока, индуцирующего эти вихревые токи.
Уравнения Максвелла в веществе в интегральной и дифференциальной форме.
Уравнения Максвелла в интегральной форме.
Явление
электромагнитной индукции (по Фарадею)
связано с возбуждением переменным
магнитным полем вихревого электрического
поля. Тогда циркуляция напряженности
![]() этого
поля вдоль замкнутого контура L равна
этого
поля вдоль замкнутого контура L равна
![]() .
(6.1)
.
(6.1)
Дж. Максвелл сделал обобщение закона электромагнитной индукции: переменное магнитное поле в любой точке пространства создает вихревое электрическое поле. Другими словами, закон (6.1) справедлив для любого замкнутого (не только проводящего) контура, произвольно выбранного в переменном магнитном поле. Так как
![]() ,
,
то (6.1) перепишется как
![]() .
(6.2)
.
(6.2)
Формула (б.2) выражает первое уравнение Максвелла в интегральной форме.
Закон
полного тока, записанный в виде
![]() говорит
о том, что вихревое магнитное поле
создается токами проводимости, где
говорит
о том, что вихревое магнитное поле
создается токами проводимости, где
![]() пров
- плотность токов проводимости. Максвелл
сделал предположение, что источником
возникновения вихревого магнитного
поля является также переменное
электрическое поле. Для возникновения
такого тока в пространстве Максвелл
ввел понятие тока смещения, плотность
которого
см
= d
пров
- плотность токов проводимости. Максвелл
сделал предположение, что источником
возникновения вихревого магнитного
поля является также переменное
электрическое поле. Для возникновения
такого тока в пространстве Максвелл
ввел понятие тока смещения, плотность
которого
см
= d![]() /dt,
где
-
вектор электрического смещения. Например,
плотность тока смещения в диэлектрике
/dt,
где
-
вектор электрического смещения. Например,
плотность тока смещения в диэлектрике
![]() -
плотность тока смещения в вакууме, d
-
плотность тока смещения в вакууме, d![]() /dt
- плотность тока поляризации (
-
вектор поляризации). Тогда с учетом тока
смещения обобщенный закон полного тока
выразится так:
/dt
- плотность тока поляризации (
-
вектор поляризации). Тогда с учетом тока
смещения обобщенный закон полного тока
выразится так:
![]() .
(6.3)
.
(6.3)
Формула (6.3) являются вторым уравнением Максвелла в интегральной форме. Она показывает, что магнитное поле возбуждается токами проводимости и переменными электрическими полями.
С
учетом теоремы Гаусса для электростатического
поля
![]() (?
- объемная плотность электрического
заряда внутри замкнутой поверхности
S, ограничивающей объем среды V) и
постоянного магнитного поля
(?
- объемная плотность электрического
заряда внутри замкнутой поверхности
S, ограничивающей объем среды V) и
постоянного магнитного поля
![]() ,
уравнения Максвелла в интегральной
форме запишутся в виде
,
уравнения Максвелла в интегральной
форме запишутся в виде

Уравнения Максвелла рассматривают поля, создаваемые макроскопическими зарядами и токами, сосредоточенными в объемах V, значительно больших отдельных молекул, и на расстояниях, значительно больших линейных размеров молекул. В этом смысле теория Максвелла является макроскопической теорией электромагнитных полей.
Уравнения Максвелла в дифференциальной форме
Используя
математические формулы, выражающие
теорему Стокса
![]() и
теорему Гаусса
и
теорему Гаусса
![]() ,
можно формулы (6.4) представить так:
,
можно формулы (6.4) представить так:
 (6.5)
(6.5)
Формулы
(6.5) называются уравнениями Максвелла
для электромагнитного поля в
дифференциальной форме. Эти уравнения
отражают тот факт, что в покоящихся
средах переменное магнитное поле
порождает вихревое электрическое поле
и обратно, переменное электрическое
поле порождает магнитное поле.
Доказывается, что уравнения Максвелла
инвариантны относительно преобразований
Лоренца. Векторы
и
![]() электромагнитного
поля можно выразить через скалярный ?
и векторный ? потенциалы
электромагнитного
поля можно выразить через скалярный ?
и векторный ? потенциалы
![]() ,
которые удовлетворяют уравнениям
,
которые удовлетворяют уравнениям
![]() ,
(6.6)
,
(6.6)
где
![]() -
оператор Лапласа. Эти уравнения будут
использованы при анализе электромагнитных
волн в средах. Энергия электромагнитного
поля локализована в пространстве с
объемной плотностью
-
оператор Лапласа. Эти уравнения будут
использованы при анализе электромагнитных
волн в средах. Энергия электромагнитного
поля локализована в пространстве с
объемной плотностью
![]() .
(6.7)
.
(6.7)
При этом количество энергии, переносимое через единицу поверхности, перпендикулярной к направлению распространения энергии, за единицу времени, определяется вектором Пойнтинга
= [ ]. (6.8)
Векторы , и взаимно перпендикулярны. Величина вектора Пойнтинга определяет плотность потока энергии. Закон сохранения энергии для электромагнитного поля определяется уравнением для объемной плотности энергии W
div + dW/dt = 0. (6.9)
Свойства
электромагнитного поля различны в
разных инерциальных системах отсчета.
Например, если инерциальная система
отсчета К неподвижна, а другая инерциальная
система К'
движется равномерно и прямолинейно
относительно К со скоростью v и в системе
К' отсутствует магнитное поле (
/
= 0), то в системе К
=[![]()
![]() ];
если же в системе К' отсутствует
электрическое поле (E' = 0), то в системе
К
=
-[
]
. Таким образом, относительность магнитных
и электрических полей проявляется в
том, что одно из полей (электрическое
или магнитное) может отсутствовать в
одной инерциальной системе отсчета и
присутствовать в другой инерциальной
системе отсчета.
];
если же в системе К' отсутствует
электрическое поле (E' = 0), то в системе
К
=
-[
]
. Таким образом, относительность магнитных
и электрических полей проявляется в
том, что одно из полей (электрическое
или магнитное) может отсутствовать в
одной инерциальной системе отсчета и
присутствовать в другой инерциальной
системе отсчета.
Квазистационарные токи. Импеданс. Колебательный контур. Добротность контура.
Квазистационарный ток, относительно медленно изменяющийся переменный ток, для мгновенных значений которого с достаточной точностью выполняются законы постоянных токов (прямая пропорциональность между током и напряжением — Ома закон, Кирхгофа правила и др.). Подобно постоянным токам, К. т. имеет одинаковую силу тока во всех сечениях неразветвлённой цепи. Однако при расчёте К. т. (в отличие от расчёта цепей постоянного тока) необходимо учитывать возникающую при изменениях тока эдс индукции. Индуктивности, ёмкости, сопротивления ветвей цепи К. т. могут считаться сосредоточенными параметрами.
Для того чтобы данный переменный ток можно было считать К. т., необходимо выполнение условия квазистационарности, которое для синусоидальных переменных токов сводится к малости геометрических размеров электрической цепи по сравнению с длиной волны рассматриваемого тока. Токи промышленной частоты, как правило, можно рассматривать как К. т. (частоте 50 гц соответствует длина волны ~ 6000 км). Исключение составляют токи в линиях дальних передач, в которых условие квазистационарности вдоль линии не выполняется.
Для того чтобы данный переменный ток можно было считать К. т., необходимо выполнение условия квазистационарности (см. Квазистационарный процесс),которое для синусоидальных переменных токов сводится к малости геометрических размеров электрической цепи по сравнению с длиной волны рассматриваемого тока. Токи промышленной частоты, как правило, можно рассматривать как К. т. (частоте 50 гц соответствует длина волны ~ 6000 км). Исключение составляют токи в линиях дальних передач, в которых условие квазистационарности вдоль линии не выполняется.
Импеданс - это комплексное сопротивление двухполюсника для гармонического сигнала. Это понятие ввёл физик и математик О. Хевисайд. Импедансом называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник. При этом импеданс не должен зависеть от времени: если время t в выражении для импеданса не сокращается, значит для данного двухполюсника понятие импеданса не применимо.
Колебательный
контур,
электрическая цепь, содержащая катушку
индуктивности и конденсатор, в которой
могут возбуждаться электрические
колебания. Если в некоторый момент
времени зарядить конденсатор до
напряжения V0,
то энергия, сосредоточенная в электрическом
поле конденсатора, равна Ес
=
![]() ,
где С — ёмкость конденсатора. При
разрядке конденсатора в катушке потечёт
ток I,
который будет возрастать до тех пор,
пока конденсатор полностью не разрядится.
В этот момент электрическая энергия К.
к. Ec
=
0, а магнитная, сосредоточенная в катушке,
EL=
,
где С — ёмкость конденсатора. При
разрядке конденсатора в катушке потечёт
ток I,
который будет возрастать до тех пор,
пока конденсатор полностью не разрядится.
В этот момент электрическая энергия К.
к. Ec
=
0, а магнитная, сосредоточенная в катушке,
EL=
![]() ,
где L
—
индуктивность катушки, I0
— максимальное значение тока. Затем
ток в катушке начинает падать, а напряжение
на конденсаторе возрастать по абсолютной
величине, но с противоположным знаком.
Спустя некоторое время ток через
индуктивность прекратится, а конденсатор
зарядится до напряжения — V0.
Энергия К. к. вновь сосредоточится в
заряженном конденсаторе. Далее процесс
повторяется, но с противоположным
направлением тока. Напряжение на
обкладках конденсатора меняется по
закону V
= V0
cos w0t,
а
ток в катушке индуктивности I
= I0
sin w0t,
т. е. в К. к. возбуждаются собственные
гармонические колебания напряжения и
тока с частотой w0
= 2 p/T0,
где T0
—
период собственных колебаний, равный
T0
=
2p
,
где L
—
индуктивность катушки, I0
— максимальное значение тока. Затем
ток в катушке начинает падать, а напряжение
на конденсаторе возрастать по абсолютной
величине, но с противоположным знаком.
Спустя некоторое время ток через
индуктивность прекратится, а конденсатор
зарядится до напряжения — V0.
Энергия К. к. вновь сосредоточится в
заряженном конденсаторе. Далее процесс
повторяется, но с противоположным
направлением тока. Напряжение на
обкладках конденсатора меняется по
закону V
= V0
cos w0t,
а
ток в катушке индуктивности I
= I0
sin w0t,
т. е. в К. к. возбуждаются собственные
гармонические колебания напряжения и
тока с частотой w0
= 2 p/T0,
где T0
—
период собственных колебаний, равный
T0
=
2p
![]() .
В К. к. дважды за период происходит
перекачка энергии из электрического
поля конденсатора в магнитное поле
катушки индуктивности и обратно.
.
В К. к. дважды за период происходит
перекачка энергии из электрического
поля конденсатора в магнитное поле
катушки индуктивности и обратно.
В
реальных К. к., однако, часть энергии
теряется. Она тратится на нагрев проводов
катушки, обладающих активным сопротивлением,
на излучение электромагнитных волн в
окружающее пространство и потери в
диэлектриках,
что приводит к затуханию колебаний.
Амплитуда колебаний постепенно
уменьшается, так что напряжение на
обкладках конденсатора меняется уже
по закону: V=V0e-dtcoswt,
где
коэффициент d = R/2L
—
показатель (коэффициент) затухания, а
w =
![]() —
частота затухающих колебаний. Т. о.,
потери приводят к изменению не только
амплитуды колебаний, но и их периода Т
= 2
p/w.
Качество К. к. обычно характеризуют его
добротностью
—
частота затухающих колебаний. Т. о.,
потери приводят к изменению не только
амплитуды колебаний, но и их периода Т
= 2
p/w.
Качество К. к. обычно характеризуют его
добротностью
![]() .
Величина Q
определяет число колебаний, которое
совершит К. к. после однократной зарядки
его конденсатора, прежде чем амплитуда
колебаний уменьшится в е
раз (е
— основание натуральных логарифмов).
.
Величина Q
определяет число колебаний, которое
совершит К. к. после однократной зарядки
его конденсатора, прежде чем амплитуда
колебаний уменьшится в е
раз (е
— основание натуральных логарифмов).
Если включить в К. к. генератор с переменной эдс: U = U0 cosWt (), то в К. к. возникнет сложное колебание, являющееся суммой его собственных колебаний с частотой w0 и вынужденных с частотой W. Через некоторое время после включения генератора собственные колебания в контуре затухнут и останутся только вынужденные. Амплитуда этих стационарных вынужденных колебаний определяется соотношением
 ,
т. е. зависит не только от амплитуды
внешней эдс U0,
но и от её частоты W. Зависимость амплитуды
колебаний в К. к.
,
т. е. зависит не только от амплитуды
внешней эдс U0,
но и от её частоты W. Зависимость амплитуды
колебаний в К. к.
от частоты внешней эдс называется резонансной характеристикой контура. Резкое увеличение амплитуды имеет место при значениях W, близких к собственной частоте w 0 К. к. При W =w0 амплитуда колебаний Vmakc в Q раз превышает амплитуду внешней эдс U. Т. к. обычно 10 < Q < 100, то К. к. позволяет выделить из множества колебаний те, частоты которых близки к w 0. Именно это свойство (избирательность) К. к. используется на практике. Область (полоса) частот DW вблизи w 0, в пределах которой амплитуда колебаний в К. к. меняется мало, зависит от его добротности Q. Численно Q равно отношению частоты w0 собственных колебаний к ширине полосы частот DW.
Для повышения избирательности К. к. необходимо увеличивать Q. Однако рост добротности сопровождается увеличением времени установления колебаний в К. к. Изменения амплитуды колебаний в контуре с высокой добротностью не успевают следовать за быстрыми изменениями амплитуды внешней эдс. Требование высокой избирательности К. к. противоречит требованию передачи быстро изменяющихся сигналов. Поэтому, например, в усилителях телевизионных сигналов искусственно снижают добротность К. к. Часто используются схемы с двумя или несколькими связанными между собой К. к. Такие системы при правильно подобранных связях обладают почти прямоугольной резонансной кривой (пунктир,).
Кроме описанных линейных К. к. с постоянными L и С, применяются нелинейные К. к., параметры которых L или С зависят от амплитуды колебаний. Например, если в катушку индуктивности К. к. вставлен железный сердечник, то намагниченность железа, а с ним и индуктивность L катушки меняется с изменением тока, текущего через неё. Период колебания в таком К. к. зависит от амплитуды, поэтому резонансная кривая приобретает наклон, а при больших амплитудах становится неоднозначной (). В последнем случае имеют место скачки амплитуды при плавном изменении частоты W внешней эдс. Нелинейные эффекты проявляются тем сильнее, чем меньше потери в К. к. В К. к. с низкой добротностью нелинейность вообще не сказывается на характере резонансной кривой.
 Колебательный
контур
Колебательный
контур
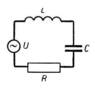 Колебательный
контур с источником переменной эдс
Колебательный
контур с источником переменной эдс
 Резонансная
кривая колебательного контура
Резонансная
кривая колебательного контура
 Резонансная
кривая нелинейного контура
Резонансная
кривая нелинейного контура
Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Общая формула для добротности любой колебательной системы:
![]() ,
,
где:
![]() —
резонансная частота
колебаний
—
резонансная частота
колебаний
![]() —
энергия, запасённая
в колебательной системе
—
энергия, запасённая
в колебательной системе
![]() —
рассеиваемая
мощность.
—
рассеиваемая
мощность.
Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах - на зеркалах.
Для последовательного Колебательного контура в RLC цепях, в котором все три элемента включены последовательно:
 ,
,
где
,
![]() и
и
![]() —
сопротивление,
индуктивность
и ёмкость
резонансной цепи, соответственно.
—
сопротивление,
индуктивность
и ёмкость
резонансной цепи, соответственно.
Для параллельного контура, в котором индуктивность, емкость и сопротивление включены параллельно:
 ,
,
Для
электрической цепи гораздо проще
измерить амплитуду (ток или напряжение),
чем энергию или мощность. Поскольку
мощность и энергия пропорциональны
квадрату амплитуды осцилляции, полоса
на АЧХ будет
![]() от
пика (примерно −3 дБ, а 1/2 это −6 дБ).
Поэтому чаще используется другое
эквивалентное определение добротности,
которое связывает ширину амплитудной
резонансной кривой
от
пика (примерно −3 дБ, а 1/2 это −6 дБ).
Поэтому чаще используется другое
эквивалентное определение добротности,
которое связывает ширину амплитудной
резонансной кривой
![]() по
уровню
с
круговой частотой резонанса
по
уровню
с
круговой частотой резонанса
![]() :
:
![]() ,
,
где:
![]() -
коэффициент затухания, равный полуширине
резонансной кривой,
-
коэффициент затухания, равный полуширине
резонансной кривой,
![]() —
число колебаний за время релаксации.
—
число колебаний за время релаксации.
Электродвигатели. Основные законы.
Кинематика колебаний. Гармоническое колебание и его характеристики: амплитуда, период и частота, фаза. Сложение взаимно-перпендикулярных гармонических колебаний. Фигуры Лиссажу.
Найдем результат
сложения двух гармонических колебаний
одинаковой частоты ω, которые происходят
во взаимно перпендикулярных направлениях
вдоль осей х и у. Начало отсчета для
простоты выберем так, чтобы начальная
фаза первого колебания была равна нулю,
и запишем это в виде
![]() (1)
где α — разность фаз обоих колебаний,
А и В равны амплитудам складываемых
колебаний. Уравнение траектории
результирующего колебания определим
исключением из формул (1) времени t.
Записывая складываемые колебания как
(1)
где α — разность фаз обоих колебаний,
А и В равны амплитудам складываемых
колебаний. Уравнение траектории
результирующего колебания определим
исключением из формул (1) времени t.
Записывая складываемые колебания как
![]()
![]()
и заменяя во втором
уравнении
![]() на
на
![]() и
и
![]() на
на
![]() ,
найдем после несложных преобразований
уравнение эллипса, у которого оси
ориентированы произвольно относительно
координатных осей:
,
найдем после несложных преобразований
уравнение эллипса, у которого оси
ориентированы произвольно относительно
координатных осей:
![]() (2)
Поскольку траектория результирующего
колебания имеет форму эллипса, то такие
колебания называются эллиптически
поляризованными.
Размеры осей эллипса и его ориентация
зависят от амплитуд складываемых
колебаний и разности фаз α. Рассмотрим
некоторые частные случаи, которые
представляют для нас физический интерес:
1) α = mπ (m=0, ±1, ±2, ...). В этом случае
эллипс становится отрезком прямой
(2)
Поскольку траектория результирующего
колебания имеет форму эллипса, то такие
колебания называются эллиптически
поляризованными.
Размеры осей эллипса и его ориентация
зависят от амплитуд складываемых
колебаний и разности фаз α. Рассмотрим
некоторые частные случаи, которые
представляют для нас физический интерес:
1) α = mπ (m=0, ±1, ±2, ...). В этом случае
эллипс становится отрезком прямой
![]() (3)
где знак плюс соответствует нулю и
четным значениям m (рис. 1а), а знак минус
— нечетным значениям m (рис. 2б).
Результирующее колебание есть
гармоническое колебание с частотой ω
и амплитудой , которое совершается вдоль
прямой (3), составляющей с осью х угол .
В этом случае имеем дело с линейно
поляризованными колебаниями;
2) α = (2m+1)(π/2) (m=0, ± 1, ±2,...). В этом случае
уравнение станет иметь вид
(3)
где знак плюс соответствует нулю и
четным значениям m (рис. 1а), а знак минус
— нечетным значениям m (рис. 2б).
Результирующее колебание есть
гармоническое колебание с частотой ω
и амплитудой , которое совершается вдоль
прямой (3), составляющей с осью х угол .
В этом случае имеем дело с линейно
поляризованными колебаниями;
2) α = (2m+1)(π/2) (m=0, ± 1, ±2,...). В этом случае
уравнение станет иметь вид
![]() (4)
Это есть уравнение эллипса, у которого
оси совпадают с осями координат, а его
полуоси равны соответствующим амплитудам
(рис. 2). Если А=В, то эллипс (4) превращается
в окружность. Такие колебания называются
циркулярно
поляризованными колебаниями
или колебаниями,
поляризованными по кругу.
(4)
Это есть уравнение эллипса, у которого
оси совпадают с осями координат, а его
полуоси равны соответствующим амплитудам
(рис. 2). Если А=В, то эллипс (4) превращается
в окружность. Такие колебания называются
циркулярно
поляризованными колебаниями
или колебаниями,
поляризованными по кругу.

Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ).
Лиссажу фигуры, замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822—80). Вид Л. ф. зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов Л. ф. представляют собой эллипсы, которые при разности фаз 0 или p вырождаются в отрезки прямых, а при разности фаз p/2 и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах Л. ф. не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются Л. ф. более сложной формы.
Л. ф. можно наблюдать, например, на экране катодного осциллографа; они получаются в результате перемещения светящейся точки, если к двум парам отклоняющих пластин подведены переменные напряжения с равными или кратными периодами. Наблюдение Л. ф. — удобный метод исследования соотношений между периодами и фазами колебаний, а также и формы колебаний.

Сложение коллинеарных колебаний с близкими частотами. Биения.
Биения,
колебания с периодически меняющейся
амплитудой, возникающие в результате
наложения двух гармонических
колебаний
с несколько различными, но близкими
частотами. Б. возникают вследствие того,
что разность фаз между двумя колебаниями
с различными частотами всё время
изменяется так, что оба колебания
оказываются в какой-то момент времени
в фазе, через некоторое время — в
противофазе, затем снова в фазе и т.д.
Если А1
и А2
— амплитуды двух накладывающихся
колебаний, то при одинаковых фазах
колебаний амплитуда результирующего
колебания достигает наибольшего значения
A1
+ A2,
а когда фазы колебаний противоположны,
амплитуда результирующего колебания
падает до наименьшего значения A1
— A2.
В простейшем случае, когда амплитуды
обоих колебаний равны, их сумма достигает
значения 2А при одинаковых фазах колебаний
и падает до нуля, когда они противоположны
по фазе (рис.).
Результат наложения колебания можно
записать в виде:

![]()
где w1 и w2 — соответственно угловые частоты двух накладывающихся гармонических колебаний (начальные фазы обоих колебаний полагаются равными нулю, т.к. они не играют роли в образовании Б.; играет роль только разность фаз между обоими колебаниями, которая всё время меняется от 0 до 2p).
Если w1 и w2 мало различаются, то в выражении (1) величину
![]()
можно рассматривать как медленно меняющуюся амплитуду колебания
![]()
Угловая частота W = w1 — w2; называется угловой частотой Б. Именно, поскольку частота w1 + w2 много больше частоты Б., мы вправе рассматривать переменную величину (2) как амплитуду колебаний (3), т.к. величина (2), хотя и не постоянная (какой должна быть амплитуда), но меняющаяся лишь медленно. По мере сближения частот w1 и w2 частота Б. уменьшается, исчезая при w1 ® w2 ("нулевые" Б.), этим пользуются при настройке музыкальных инструментов. В радиотехнике гетеродинный приём называется "приёмом на Б.". Суть его заключается в том, что если 2 гармонических колебания подать на нелинейный элемент — детектор, то получается гармоническое колебание с разностной частотой W. Т. к. разностная частота много ниже частоты принимаемых колебаний, то при некоторых соотношениях частот она может восприниматься на слух.
Динамика механических колебаний. Тело на пружине, Превращения энергии при свободных механических колебаниях.
При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругих деформаций пружины. Для математического маятника – это энергия в поле тяготения Земли.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по закону инерции. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д. Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. Для груза на пружине (см. §2.2):
|
|
Для малых колебаний математического маятника (см. §2.3):
|
|
Здесь hm – максимальная высота подъема маятника в поле тяготения Земли, xm и υm = ω0xm – максимальные значения отклонения маятника от положения равновесия и его скорости. Превращения энергии при свободных механических колебаниях в отсутствие трения можно проиллюстрировать графически. Рассмотрим в качестве примера колебания груза массой m на пружине жесткости k. Пусть смещение x(t) груза из положения равновесия и его скорость υ(t) изменяются со временем по законам:
|
υ(t) = –ωxm sin (ω0t). |
Следовательно,
|
|
На
рис. 2.4.1 изображены графики функций
Ep(t) и Ek(t). Потенциальная и кинетическая
энергии два раза за период колебаний
![]() достигают
максимальных значений. Сумма
достигают
максимальных значений. Сумма
![]() остается
неизменной.
остается
неизменной.
|
Рисунок 2.4.1. Превращения энергии при свободных колебаниях. |
В реальных условиях любая колебательная система находится под воздействием сил трения (сопротивления). При этом часть механической энергии превращается во внутреннюю энергию теплового движения атомов и молекул, и колебания становятся затухающими (рис. 2.4.2).
|
Рисунок 2.4.2. Затухающие колебания. |
Скорость затухания колебаний зависит от величины сил трения. Интервал времени τ, в течении которого амплитуда колебаний уменьшается в e ≈ 2,7 раз, называется временем затухания. Частота свободных колебаний зависит от скорости затухания колебаний. При возрастании сил трения собственная частота уменьшается. Однако, изменение собственной частоты становится заметным лишь при достаточно больших силах трения, когда собственные колебания быстро затухают. Важной характеристикой колебательной системы, совершающей свободные затухающие колебания, является добротность Q. Этот параметр определяется как число N полных колебаний, совершаемых системой за время затухания τ, умноженное на π:
|
Чем медленнее происходит затухание свободных колебаний, тем выше добротность Q колебательной системы. Добротность колебательной системы, определенная по затуханию колебаний на рис. 2.4.2, приблизительно равна 15. Добротности механических колебательных систем могут быть очень высокими – порядка нескольких сотен и даже тысяч. Понятие добротности имеет глубокий энергетический смысл. Можно определить добротность Q колебательной системы следующим энергетическим соотношением:
|
Таким образом, добротность характеризует относительную убыль энергии колебательной системы из-за наличия трения на интервале времени, равном одному периоду колебаний.
Крутильные колебания. Физический и математический маятники.
КРУТИЛЬНЫЕ КОЛЕБАНИЯ - механич. колебания, при к-рых упругие элементы испытывают деформации сдвига. Имеют место в разл. машинах с вращающимися валами: в поршневых двигателях, турбинах, генераторах, редукторах, трансмиссиях транспортных машин.
К. к. возникают в результате неравномерности периодич. момента как движущих сил, так и сил сопротивления. Неравномерность крутящего момента вызывает неравномерность изменения угловой скорости вала, т. е. то ускорение, то замедление вращения. Обычно вал представляет собой чередование участков с малой массой и упругой податливостью с более жёсткими участками, на к-рых закреплены значит. массы. В каждом сечении вала будет своя степень неравномерности вращения, поскольку в одинаковый промежуток времени массы проходят разные углы и, следовательно, движутся с разными скоростями, что создаёт переменное кручение вала и динамич. знакопеременные напряжения, гл. обр. касательные.
При совпадении частот собств. колебаний системы с частотой периодич. крутящего момента движущих сил и сил сопротивления возникают резонансные колебания. В этом случае повышается уровень динамич. переменных напряжений; возрастает акустич. шум, излучаемый работающей машиной. Динамич. знакопеременные напряжения при неправильно выбранных (заниженных) размерах вала, недостаточной прочности его материала и возникновении резонанса могут превысить предел выносливости, что приведёт к усталости материала вала и его разрушению.
При расчёте К. к. валов машин часто пользуются расчётной схемой с двумя дисками, соединёнными упругим стержнем, работающим на кручение. В этом случае собств. частота
![]()
где
I1
- момент
инерции
1-го диска, I2
- момент инерции 2-го диска, С
-крутильная жёсткость стержня, Для
круглого стержня диаметром d
и длиной l
С![]() где G - модуль сдвига. Более сложные
расчётные схемы содержат большее число
дисков, соединённых стержнями и образующих
последоват. цепи, а иногда - разветвлённые
и кольцевые цепи. Расчёт собств. частот
форм и вынужденных К. к. по этим расчётным
схемам производится на ЭВМ.
где G - модуль сдвига. Более сложные
расчётные схемы содержат большее число
дисков, соединённых стержнями и образующих
последоват. цепи, а иногда - разветвлённые
и кольцевые цепи. Расчёт собств. частот
форм и вынужденных К. к. по этим расчётным
схемам производится на ЭВМ.
Др.
примером К. к. является крутильный
маятник, к-рый представляет собой диск,
закреплённый на одном конце стержня,
работающего на кручение и жёстко
заделанного др. концом. Собств. частота
такого маятника![]() где I
- момент инерции диска. Приборы с
использованием крутильного маятника
применяют для определения модуля
упругости
при сдвиге, коэф. внутр. трения твёрдых
материалов при сдвиге, коэф. вязкости
жидкости.
где I
- момент инерции диска. Приборы с
использованием крутильного маятника
применяют для определения модуля
упругости
при сдвиге, коэф. внутр. трения твёрдых
материалов при сдвиге, коэф. вязкости
жидкости.
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

Таким маятником
можно считать тяжелый шар массой m,
подвешенный на тонкой нити, длина l
которой намного больше размеров шара.
Если его отклонить на угол α (рис.) от
вертикальной линии, то под влиянием
силы F – одной из составляющих веса Р
он будет совершать колебания. Другая
составляющая
![]() ,
направленная вдоль нити, не учитывается,
т.к. уравновешивается силой натяжения
нити. При малых углах смещения
,
направленная вдоль нити, не учитывается,
т.к. уравновешивается силой натяжения
нити. При малых углах смещения
![]() и,
тогда координату х можно отсчитывать
по горизонтальному направлению. Из рис.
видно, что составляющая веса,
перпендикулярная нити, равна
и,
тогда координату х можно отсчитывать
по горизонтальному направлению. Из рис.
видно, что составляющая веса,
перпендикулярная нити, равна
![]()
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
![]()
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы
относительно точки О:
![]() ,
и момент инерции:
M
= FL .
Момент
инерции J
в данном случае
Угловое ускорение:
,
и момент инерции:
M
= FL .
Момент
инерции J
в данном случае
Угловое ускорение:
![]()
С учетом этих
величин имеем:
![]()
или
|
Его решение
 ,
,
где
|
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
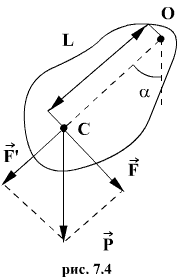
При небольших углах отклонения α (рис.) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
![]() .
Момент силы: определить в явном виде
нельзя. С учетом всех величин, входящих
в исходное дифференциальное уравнение
колебаний физического маятника имеет
вид:
.
Момент силы: определить в явном виде
нельзя. С учетом всех величин, входящих
в исходное дифференциальное уравнение
колебаний физического маятника имеет
вид:
|
|
Решение этого
уравнения

Определим длину l
математического маятника, при которой
период его колебаний равен периоду
колебаний физического маятника, т.е.
![]() или
или
![]() .
Из
этого соотношения определяем
.
Из
этого соотношения определяем
![]()
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
Свободные затухающие колебания: коэффициент и логарифмический декремент затухания.
Всякий реальный колебательный контур обладает сопротивлением. Энергия электрических колебаний в таком контуре постепенно расходуется на нагревание сопротивления, переходя в джоулево тепло, вследствие чего колебания затухают.

Уравнение свободных затухающих колебаний можно получить, исходя из того, что в отсутствии внешнего источника напряжения, сумма падений напряжений на индуктивности, емкости и сопротивлении равна нулю для любого момента времени:
![]()
или, поскольку![]() ,
,
![]() .
.
Введя обозначение
![]() ,
,
этому уравнению можно придать вид:
![]() ,
,
где
![]() .
.
Решение полученного уравнения имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
где
|
|
|
|
Мы видим, что частота свободных затухающих колебаний ω′ меньше собственной частоты ω0. Подставив значения ω0 и β, получим:
![]()
Амплитуда затухающих колебаний заряда конденсатора q0(t) уменьшается со временем по экспоненциальному закону (рис.16.4). Коэффициент β называется коэффициентом затухания.

Рис.16.4. Изменение заряда конденсатора со временем в RLC-контуре.
Затухание колебаний принято характеризовать декрементом колебаний λ, определяемым как:
![]() .
.
Легко видеть, что декремент колебаний обратен по величине числу колебаний Ne, совершаемых за время, в течение которого амплитуда колебаний уменьшается в е раз: λ=1/Ne. Добротностью колебательного контура называется величина:
![]()
Из этой формулы видно, что добротность тем выше, чем меньше коэффициент затухания β. При малых затуханиях (λ<<1) можно приближенно считать, что
![]() .
.
Амплитуда тока в
контуре, как и заряд на конденсаторе,
убывает со временем по закону
![]() .
Энергия W, запасенная в контуре,
пропорциональна квадрату амплитуды
тока (или квадрату напряжения на
конденсаторе). Следовательно, W убывает
со временем по закону e-2βt. Относительное
уменьшение энергии за период колебания
Т (при малом затухании) есть:
.
Энергия W, запасенная в контуре,
пропорциональна квадрату амплитуды
тока (или квадрату напряжения на
конденсаторе). Следовательно, W убывает
со временем по закону e-2βt. Относительное
уменьшение энергии за период колебания
Т (при малом затухании) есть:
![]() .
.
Таким образом, потери энергии в колебательном контуре тем меньше, чем выше его добротность.
Собственные частоты. Вынужденные колебания: уравнение движения и его решение.
Перейдем к рассмотрению колебаний в системе, на которую действует некоторое переменное внешнее поле; такие колебания называют вынужденными в отличие от рассмотренных в предыдущем параграфе так называемых свободных колебаний. Поскольку колебания предполагаются по-прежнему малыми, то тем самым подразумевается, что внешнее поле достаточно слабо, в противном случае оно могло бы вызвать слишком большое смещение x.
В этом случае наряду с собственной потенциальной энергией (1/2)kx2 система обладает еще потенциальной энергией Ue(x,t), связанной с действием внешнего поля. Разлагая этот дополнительный член в ряд по степеням малой величины x, получим
Ue
(x,t)
≈ Ue(0,t)
+ x
![]()
 .
.
Первый член является функцией только от времени и потому может быть опущен в лагранжевой функции (как полная производная по t от некоторой другой функции времени). Во втором члене −∂Ue/∂x есть внешняя «сила», действующая на систему в положении равновесия и являющаяся заданной функцией времени; обозначим ее как F(t). Таким образом, в потенциальной энергии появляется член −xF(t), так что функция Лагранжа системы будет
L
=
![]() −
−
![]() +
xF
(t).
+
xF
(t).
Соответствующее уравнение движения есть
+ kx = F (t),
или
![]() +
ω2x
=
+
ω2x
=
![]() F
(t),
F
(t),
где мы снова ввели частоту w свободных колебаний.
Как известно, общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами получается в виде суммы двух выражений: x=x0+x1, где x0 — общее решение однородного уравнения, а x1 — частный интеграл неоднородного уравнения. В данном случае x0 представляет собой рассмотренные в предыдущем параграфе свободные колебания.
Рассмотрим
имеющий особый интерес случай, когда
вынуждающая сила тоже является простой
периодической функцией времени с
некоторой частотой
![]() :
:
F (t) = ƒ cos ( t + β).
Частный интеграл уравнения ищем в виде x1=b cos( t+β) с тем же периодическим множителем. Подстановка в уравнение дает: b=ƒ⁄[m(ω2− 2)]; прибавляя решение однородного уравнения, получим общий интеграл в виде
x
= α
cos (ωt
+
![]() )
+
)
+
![]() cos
(
t
+ β).
cos
(
t
+ β).
Произвольные постоянные а и а определяются из начальных условий.
Таким образом, под действием периодической вынуждающей силы система совершает движение, представляющее собой совокупность двух колебаний — с собственной частотой системы ω и с частотой вынуждающей силы .
Решение неприменимо в случае так называемого резонанса, когда частота вынуждающей силы совпадает с собственной частотой системы. Для нахождения общего решения уравнения движения в этом случае перепишем выражение с соответствующим переобозначением постоянных в виде
x = α cos (ωt + ) + [cos ( t + β) − cos (ωt + β)].
Фазовые и амплитудные резонансные кривые. Резонанс. Добротность осциллятора.
Фазовая резонансная кривая. Как следует из уравнения (13.6), сдвиг по фазе между силой и смещением зависит от соотношения частот собственной и вынуждающей силы, а также от значения коэффициента затухания d (см. рис. 13.5). При значении w = w0 смещение отстает от силы на p/2. Это означает, что в момент, когда сила достигает своего максимального значения, смещение равно нулю, а когда сила равна нулю смещение максимально. С возрастанием частоты отставание смещения от силы растет и при очень больших частотах приближается к p, т.е. сила и смещение колеблются в противофазе.
Фазовые соотношения между смещением и силой позволяют более глубоко понять сущность явления резонанса с точки зрения энергетических соображений. Пусть при w = w0 сила и смещение подчиняются следующим законам:
F = F0·cos(w0·t); x = A·sin(w0·t).
Тогда уравнение для скорости колеблющейся частицы (осциллятора) имеет вид:
x' = u = - A·w·cos(w0·t).
Из этих соотношений видно, что скорость u и сила колеблются в фазе. Следовательно, мощность, сообщаемая осциллятору внешней силой, равна N = F·u. Ее значение положительно в любой момент времени, следовательно, работа внешней силы достигает своего максимального значения. Энергия в этом случае направлена на преодоление сил трения.
В случае w = wрез величина j по модулю несколько меньше, чем p/2, но за счет большего, чем в случае w = w0 значения скорости осциллятора интегральная величина работы за период колебаний максимальна и
резонанс характеризуется наличием максимально благоприятных условий для передачи энергии от источника внешней силы к осциллятору.
Самые неблагоприятные условия передачи энергии при w << w0 и w >> w0, В этих случаях фазы силы и скорости отличаются почти на p. Значит сила примерно половину времени направлена противоположно скорости и половину времени совпадает с ней. В среднем осциллятору от источника внешней силы передается незначительная энергия за период колебаний и поэтому амплитуда колебаний в этих случаях очень мала.
Амплитудная резонансная кривая. Резонанс. Построим зависимость А(w), график которой называется амплитудной резонансной кривой. Вид этой кривой зависит от величины коэффициента затухания d (см. рис. 13.4). Амплитуда, соответствующая значению частоты w = 0, называется статическим смещением. Т.к. F0 = k·Aст, то
Аст = F0/(m·w02) = F0/k. (13.7)
Из графика видно, что при определенном значении частоты вынуждающей силы амплитуда осциллятора становится максимальной.
Явление, при котором амплитуда колебаний системы достигает максимального значения, характерного для некоторого значении частоты вынуждающей силы называется резонансом.
Частота вынуждающей силы, при которой наступает данное явление, называется резонансной. Приравнивая к нулю производную выражения (13.5) по частоте и пренебрегая слагаемыми второго порядка малости, получим формулы для расчета резонансной частоты wрез и амплитуды Арез:
wрез = (w02 - 2d2)1/2; (13.8) Арез = F0/(2m·d·w0). (13.9)
При значении d = 0 амплитуда колебаний в резонансе стремится к бесконечности.
Важной характеристикой осциллятора является отношение амплитуды его колебаний в резонансе к ее статическому значению. Из формул (13.7) и (13.9) следует, что это отношение равно добротности системы:
Арез/Аст = p/d = Q, где d - логарифмический декремент затухания.
Добротность является важнейшей характеристикой резонансных свойств системы.
Рассмотрим качественно физическую картину вынужденных колебаний в различных областях частот.
а) w << w0. В уравнении движения (13.1) слагаемые, пропорциональные ускорению и скорости, много больше слагаемого wо2·х, связанного с упругой силой. Следовательно, уравнение движения сводится к следующему виду:
wо2·х = F0/m · cos(w·t); x = F0 cos(w·t)/k = F(t)/k.
Таким образом каждый момент времени смещение являлось таким, каким оно должно было бы быть, если бы сила не изменялась со временем и равнялась своему мгновенному значению. Силы трения роли не играют. Смещение совпадает по фазе с внешней силой.
б) w >> w0. При большой частоте вынуждающей силы слагаемое, обусловленное ускорением, много больше слагаемых, связанных со скоростью и упругой силой. Таким образом, силы упругости и силы трения не играют никакой роли в колебаниях. Внешняя сила действует на осциллятор так, как если бы этих сил не было. Поэтому уравнение движения имеет вид:
x'' = F0/m · cos(w·t).
Решение этого уравнения представляется формулой:
x = - F0/(m·w2) · cos(w·t) = - F(t)/(m·w2).
Смещение отстает от силы по фазе на p.
в) Случай резонанса w = w0. Слагаемое, связанное с ускорением, равно слагаемому, обусловленному упругой силой, т.е. x'' = - w2·x = - w02·x. Это значит, что ускорение создается силой упругости, а внешняя сила и сила трения взаимно компенсируются. Уравнение движения имеет вид:
2d·x' = F0/m · cos(w·t).
Решение этого уравнения представляется формулой:
x = F0/(2d·m·w0) · sin(w0·t).
Смещение отстает от силы по фазе на p/2.
 Механическая
колебательная система
Механическая
колебательная система
 Электрическая
колебательная система
Электрическая
колебательная система
 Амплитуды
смещений
Амплитуды
смещений
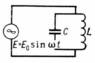 Электрическая
колебательная система
Электрическая
колебательная система
 Два
связанных электрических контура
Два
связанных электрических контура
 Резонансная
кривая с двумя максимумами
Резонансная
кривая с двумя максимумами
Резонанс (франц. resonance, от лат. resono — звучу в ответ, откликаюсь), явление резкого возрастания амплитуды вынужденных колебаний в какой-либо колебательной системе, наступающее при приближении частоты периодического внешнего воздействия к некоторым значениям, определяемым свойствами самой системы. В простейших случаях Р. наступает при приближении частоты внешнего воздействия к одной из тех частот, с которыми происходят собственные колебания в системе, возникающие в результате начального толчка. Характер явления Р. существенно зависит от свойств колебательной системы. Наиболее просто Р. протекает в тех случаях, когда периодическому воздействию подвергается система с параметрами, не зависящими от состояния самой системы (т. н. линейные системы).
Типичные черты Р.
можно выяснить, рассматривая случай
гармонического воздействия на систему
с одной степенью свободы: например, на
массу m,
подвешенную на пружине, находящуюся
под действием гармонической силы F
=
F0
coswt (рис.
1), или
электрическую цепь, состоящую из
последовательно соединённых индуктивности
L,
ёмкости С,
сопротивления R
и источника электродвижущей силы Е,
меняющейся по гармоническому закону
(рис. 2).
Для определенности в дальнейшем
рассматривается первая из этих моделей,
но всё сказанное ниже можно распространить
и на вторую модель. Примем, что пружина
подчиняется закону Гука (это предположение
необходимо, чтобы система была линейна),
т. е., что сила, действующая со стороны
пружины на массу m,равна
kx,
где х —
смещение массы от положения равновесия,
k —
коэффициент упругости (сила тяжести
для простоты не принимается во внимание).
Далее, пусть при движении масса испытывает
со стороны окружающей среды сопротивление,
пропорциональное её скорости
![]() и
коэффициенту трения b,
т. е. равное k
(это
необходимо, чтобы система оставалась
линейной). Тогда уравнение движения
массы m при
наличии гармонической внешней силы F
имеет вид:
и
коэффициенту трения b,
т. е. равное k
(это
необходимо, чтобы система оставалась
линейной). Тогда уравнение движения
массы m при
наличии гармонической внешней силы F
имеет вид:
![]() (1)
(1)
где F0
—
амплитуда колебания, w— циклическая
частота, равная 2p/Т,
Т —
период внешнего воздействия,
![]() —
ускорение массы m.
Решение этого уравнения может быть
представлено в виде суммы двух решений.
Первое из этих решений соответствует
свободным колебаниям системы, возникающим
под действием начального толчка, а
второе — вынужденным колебаниям.
Собственные колебания в системе
вследствие наличия трения и сопротивления
среды всегда затухают, поэтому по
истечении достаточного промежутка
времени (тем большего, чем меньше
затухание собственных колебаний) в
системе останутся одни только вынужденные
колебания. Решение, соответствующее
вынужденным колебаниям, имеет вид:
—
ускорение массы m.
Решение этого уравнения может быть
представлено в виде суммы двух решений.
Первое из этих решений соответствует
свободным колебаниям системы, возникающим
под действием начального толчка, а
второе — вынужденным колебаниям.
Собственные колебания в системе
вследствие наличия трения и сопротивления
среды всегда затухают, поэтому по
истечении достаточного промежутка
времени (тем большего, чем меньше
затухание собственных колебаний) в
системе останутся одни только вынужденные
колебания. Решение, соответствующее
вынужденным колебаниям, имеет вид:
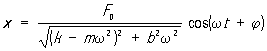 ,
(2)
,
(2)
причём tgj =
![]() .
Т. о., вынужденные колебания представляют
собой гармонические колебания с частотой,
равной частоте внешнего воздействия;
амплитуда и фаза вынужденных колебаний
зависят от соотношения между частотой
внешнего воздействия и параметрами
системы.
.
Т. о., вынужденные колебания представляют
собой гармонические колебания с частотой,
равной частоте внешнего воздействия;
амплитуда и фаза вынужденных колебаний
зависят от соотношения между частотой
внешнего воздействия и параметрами
системы.
Зависимость
амплитуды смещений при вынужденных
колебаниях от соотношения между
величинами массы m
и упругости k
легче всего проследить, полагая, что m
и k
остаются неизменными, а изменяется
частота внешнего воздействия. При очень
медленном воздействии (w ® 0) амплитуда
смещений x0"
F0/k.
С увеличением частоты w амплитуда x0
растет, т. к. знаменатель в выражении
(2) уменьшается. Когда w приближается к
значению
![]() (т.
е. к значению частоты собственных
колебаний при малом их затухании),
амплитуда вынужденных колебаний
достигает максимума — наступает Р.
Далее с увеличением w амплитуда колебаний
монотонно убывает и при w ® ¥ стремится
к нулю.
(т.
е. к значению частоты собственных
колебаний при малом их затухании),
амплитуда вынужденных колебаний
достигает максимума — наступает Р.
Далее с увеличением w амплитуда колебаний
монотонно убывает и при w ® ¥ стремится
к нулю.
Амплитуду колебаний при Р. можно приближённо определить, полагая w = . Тогда x0= F0/bw, т. е. амплитуда колебаний при Р. тем больше, чем меньше затухание b в системе (рис. 3). Наоборот, при увеличении затухания системы Р. становится всё менее резким, и если b очень велико, то Р. вообще перестаёт быть заметным. С энергетической точки зрения Р. объясняется тем, что между внешней силой и вынужденными колебаниями устанавливаются такие фазовые соотношения, при которых в систему поступает наибольшая мощность (т. к. скорость системы оказывается в фазе с внешней силой и создаются наиболее благоприятные условия для возбуждения вынужденных колебаний).
Если на линейную систему действует периодическое, но не гармоническое внешнее воздействие, то Р. наступит только тогда, когда во внешнем воздействии содержатся гармонические составляющие с частотой, близкой к собственной частоте системы. При этом для каждой отдельной составляющей явление будет протекать так же, как рассмотрено выше. А если этих гармонических составляющих с частотами, близкими к собственной частоте системы, будет несколько, то каждая из них будет вызывать резонансные явления, и общий эффект, согласно суперпозиции принципу, будет равен сумме эффектов от отдельных гармонических воздействий. Если же во внешнем воздействии не содержится гармонических составляющих с частотами, близкими к собственной частоте системы, то Р. вообще не наступает. Т. о., линейная система отзывается, "резонирует" только на гармонические внешние воздействия.
В электрических колебательных системах, состоящих из последовательно соединённых ёмкости С и индуктивности L (рис. 2), Р. состоит в том, что при приближении частот внешней эдс к собственной частоте колебательной системы, амплитуды эдс на катушке и напряжения на конденсаторе порознь оказываются гораздо больше амплитуды эдс, создаваемой источником, однако они равны по величине и противоположны по фазе. В случае воздействия гармонической эдс на цепь, состоящую из параллельно включенных ёмкости и индуктивности (рис. 4), имеет место особый случай Р. (антирезонанс). При приближении частоты внешней эдс к собственной частоте контура LC происходит не возрастание амплитуды вынужденных колебаний в контуре, а наоборот, резкое уменьшение амплитуды силы тока во внешней цепи, питающей контур. В электротехнике это явление называется Р. токов или параллельным Р. Это явление объясняется тем, что при частоте внешнего воздействия, близкой к собственной частоте контура, реактивные сопротивления обеих параллельных ветвей (ёмкостной и индуктивной) оказываются одинаковыми по величине и поэтому в обеих ветвях контура текут токи примерно одинаковой амплитуды, но почти противоположные по фазе. Вследствие этого амплитуда тока во внешней цепи (равного алгебраической сумме токов в отдельных ветвях) оказывается гораздо меньшей, чем амплитуды тока в отдельных ветвях, которые при параллельном Р. достигают наибольшей величины. Параллельный Р., так же как и последовательный Р., выражается тем резче, чем меньше активное сопротивление ветвей контура Р. Последовательный и параллельный Р. называются соответственно Р. напряжений и Р. токов.
В линейной системе с двумя степенями свободы, в частности в двух связанных системах (например, в двух связанных электрических контурах; рис. 5), явление Р. сохраняет указанные выше основные черты. Однако, т. к. в системе с двумя степенями свободы собственные колебания могут происходить с двумя различными частотами (т. н. нормальные частоты, см. Нормальные колебания), то Р. наступает при совпадении частоты гармонического внешнего воздействия как с одной, так и с другой нормальной частотой системы. Поэтому, если нормальные частоты системы не очень близки друг к другу, то при плавном изменении частоты внешнего воздействия наблюдаются два максимума амплитуды вынужденных колебаний (рис. 6). Но если нормальные частоты системы близки друг к другу и затухание в системе достаточно велико, так что Р. на каждой из нормальных частот "тупой", то может случиться, что оба максимума сольются. В этом случае кривая Р. для системы с двумя степенями свободы теряет свой "двугорбый" характер и по внешнему виду лишь незначительно отличается от кривой Р. для линейного контура с одной степенью свободы. Т. о., в системе с двумя степенями свободы форма кривой Р. зависит не только от затухания контура (как в случае системы с одной степенью свободы), но и от степени связи между контурами.
В связанных системах также существует явление, которое в известной мере аналогично явлению антирезонанса в системе с одной степенью свободы. Если в случае двух связанных контуров с различными собственными частотами настроить вторичный контур L2C2 на частоту внешней эдс, включенной в первичный контур L1C1 (рис. 5), то сила тока в первичном контуре резко падает и тем резче, чем меньше затухание контуров. Объясняется это явление тем, что при настройке вторичного контура на частоту внешней эдс в этом контуре возникает как раз такой ток, который в первичном контуре наводит эдс индукции, примерно равную внешней эдс по амплитуде и противоположную ей по фазе.
В линейных системах со многими степенями свободы и в сплошных системах Р. сохраняет те же основные черты, что и в системе с двумя степенями свободы. Однако в этом случае, в отличие от систем с одной степенью свободы, существенную роль играет распределение внешнего воздействия по отдельным координатам. При этом возможны такие специальные случаи распределения внешнего воздействия, при которых, несмотря на совпадения частоты внешнего воздействия с одной из нормальных частот системы, Р. всё же не наступает. С энергетической точки зрения это объясняется тем, что между внешней силой и вынужденными колебаниями устанавливаются такие фазовые соотношения, при которых мощность, поступающая в систему от источника возбуждения по одной координате, равна мощности, отдаваемой системой источнику по другой координате. Пример этого — возбуждение вынужденных колебаний в струне, когда внешняя сила, совпадающая по частоте с одной из нормальных частот струны, приложена в точке, которая соответствует узлу скоростей для данного нормального колебания (например, сила, совпадающая по частоте с основным тоном струны, приложена у самого конца струны). При этих условиях (вследствие того, что внешняя сила приложена к неподвижной точке струны) эта сила не совершает работы, мощность от источника внешней силы в систему не поступает и сколько-нибудь заметного возбуждения колебаний струны не возникает, т. е. Р. не наблюдается.
Р. в колебательных системах, параметры которых зависят от состояния системы, т. е. в нелинейных системах, имеет более сложный характер, чем в системах линейных. Кривые Р. в нелинейных системах могут стать резко несимметричными, и явление Р. может наблюдаться при различных соотношениях частот воздействия и частот собственных малых колебаний системы (т. н. дробный, кратный и комбинационный Р.). Примером Р. в нелинейных системах может служить т. н. феррорезонанс, т. е. резонанс в электрической цепи, содержащей индуктивность с ферромагнитным сердечником, или ферромагнитный резонанс, представляющий собой явление, связанное с Р. элементарных (атомных) магнитов вещества при приложении высокочастотного магнитного поля (см. Радиоспектроскопия).
Если внешнее воздействие производит периодические изменение энергоёмких параметров колебательной системы (например, ёмкости в электрическом контуре), то при определённых соотношениях частот изменения параметра и собственной частоты свободных колебаний системы возможно параметрическое возбуждение колебаний, или параметрический Р.
Связанные осцилляторы. Автоколебания. Параметрический резонанс.
Рассмотрим систему связанных осцилляторов (рис.). Такой системой могут служить N маятников, последовательно соединенных пружинами, или система связанных электрических контуров, или, как это показано на рис., набор материальных точек, соединенных пружинами. Если колебания происходят вдоль оси x, то положение системы N материальных точек можно характеризовать заданием N величин смещений от своих положений равновесия. Таким образом, система осцилляторов обладает N степенями свободы, В отсутствие связи между осцилляторами каждый из них может совершать независимые колебания вблизи своего положения равновесия. В этом случае колебания локализованы в определенной области пространства. Но если мы возбудим колебания в системе связанных осцилляторов, то картина будет другой.
Колебания первоначально возбужденного осциллятора, благодаря упругим свойствам пружины, возбудят колебания соседнего осциллятора, который в свою очередь передаст энергию колебаний следующему соседу и т. д. При этом колебание первоначально возбужденного осциллятора прекратится, а передаваемая энергия колебаний будет распространяться вдоль цепочки, приводя к последовательному перемещению с постоянной скоростью сгущений и разрежении упруго связанных масс. Перенос энергии колебаний в пространстве представляет собой распространение волны.
Обратим внимание на два важных обстоятельства. Во-первых, передача колебаний от одного осциллятора другому стала возможной только благодаря упругому их взаимодействию. Таким образом, физическая причина распространения волны — взаимодействие частиц. Во-вторых, сами колеблющиеся массы остаются на своих местах вблизи положений равновесия, т.е. в процессе распространения волны масса не переносится. Происходит только передача энергии колебаний посредством изменения фазы колебания соседней частицы.
Опишем распространение волны математически. При колебаниях отдельного осциллятора величина, которая характеризует его смещение от положения равновесия, зависит только от времени. Так изменяется смещение массы на пружине или угол наклона маятника, т.е. фаза свободного осциллятора зависит только от одной переменной — времени.
При прохождении волны в цепочке связанных осцилляторов смещение каждой из масс зависит от двух величин — времени и расстояния до источника колебаний. Таким образом, смещение каждой из масс
un=un(x,t)
Запишем уравнение движения произвольно выбранного n-го осциллятора цепочки. При смещении из положения равновесия на массу действует возвращающая упругая сила, равная -kun ( k — жесткость пружины). Одновременно на массу действуют упругие силы, обусловленные смещениями соседних масс: un-1 и un+1. Взаимодействиями с более удаленными соседями пренебрежем. Слева на рассматриваемую массу будет действовать сила, пропорциональная удлинению левой пружины k(un- un-1), а справа — аналогичная сила, пропорциональная уменьшению длины правой пружины — k(un - un+1). В результате уравнение движения примет вид:
 .
(3.46)
.
(3.46)
Как уже говорилось, уравнение (3.46) применимо ко многим физическим ситуациям. В частности, оно описывает колебания одномерной цепочки атомов в кристаллической решетке. В этом случае среднее расстояние между атомами является характерной для данного кристалла постоянной величиной, называемой периодом кристаллической решетки. Период решетки очень мал и по величине сравним с размерами атома. При таком расположении атомов в решетке кристалл можно рассматривать как сплошную среду, в которой распределение масс является не дискретным, как на рис., а непрерывным. Будем считать постоянную решетки бесконечно малой величиной. Тогда смещения соседних атомов на расстоянии dx un±1 мало отличаются от смещения un и их можно разложить в ряды, ограничиваясь первыми членами:
 ,
,
где знак d/dx означает производную по x в фиксированный момент времени.
После подстановки этих выражений в уравнение (3. 46), получим:

(по той же причине, что и выше, мы стали писать производную в виде d/dt).
 Спусковой
механизм часов
Спусковой
механизм часов
Автоколебания, незатухающие колебания, которые могут существовать в какой-либо системе при отсутствии переменного внешнего воздействия, причём амплитуда и период колебаний определяются свойствами самой системы. Этим А. отличаются от вынужденных колебаний, амплитуда и период которых определяются характером внешнего воздействия (приставка "авто" и указывает на то, что колебания возникают в самой системе, а не навязываются внешним воздействием). А. отличаются и от свободных колебаний (например, колебаний свободно подвешенного маятника, колебаний силы тока в электрическом контуре) тем, что, во-первых, свободные колебания постепенно затухают, во-вторых, их амплитуда зависит от первоначального "толчка", создающего эти колебания. Примерами А. могут служить колебания, совершаемые маятником часов, колебания струны в смычковых или столба воздуха в духовых музыкальных инструментах, электрические колебания в ламповом генераторе (см. Генерирование электрических колебаний). Системы, в которых возникают А., называются автоколебательными.
Автоколебательные системы во многих случаях можно разделить на 3 основных элемента: 1) колебательную систему (в узком смысле); 2) источник энергии, за счет которого поддерживаются А., и 3) устройство, регулирующее поступление энергии из источника в колебательную систему. Эти 3 основных элемента могут быть отчётливо выделены, например, в часах, в которых маятник или баланс служит колебательной системой, пружинный или гиревой завод — источником энергии, и, наконец, анкерный ход — механизмом, регулирующим поступление энергии из источника в систему. В ламповом генераторе колебательной системой служит контур, содержащий ёмкость и индуктивность и обладающий малым активным сопротивлением; выпрямитель (или батарея), питающий напряжением анод лампы, является источником энергии, а электронная лампа с элементом обратной связи — устройством, регулирующим поступление энергии из источника в колебательный контур.
В часах, например, А. осуществляются следующим образом (рис.). При прохождении качающегося балансира 1 через определённое положение (обычно дважды за период) спусковое устройство 2 и 3 подталкивает колесо балансира, сообщая ему энергию, необходимую для того, чтобы компенсировать потерю энергии за полпериода колебаний. Балансир часов совершает А. с амплитудой, целиком определяемой свойствами часового механизма. Однако для того, чтобы эти А. возникли, обычно нужно не только завести пружинный завод, но и слегка встряхнуть часы, т. е. сообщить начальный толчок балансиру. Т. о., часы — это в большинстве случаев автоколебательная система без самовозбуждения. В духовых инструментах продувание струи воздуха поддерживает А. столба воздуха в трубе инструмента, а в струнных смычковых инструментах А. поддерживаются силой трения, действующей между смычком и струной.
Чтобы колебания были незатухающими, поступающая из источника в систему энергия должна компенсировать потери энергии в самой системе. Такая компенсация происходит в целом за период колебаний; но в одни части периода поступающая энергия может превышать потери в системе, в другие, наоборот, потери в системе могут превышать поступление энергии в неё. То значение амплитуды колебаний, при котором происходит компенсация потерь в целом за период, и является стационарным (не изменяющимся со временем) значением амплитуды А. Такой баланс поступления и потерь энергии оказывается возможным только при определённых значениях амплитуды А. (в простейших случаях только при одном значении).
Обычно при значениях амплитуды колебаний, меньших стационарной, поступление энергии в систему превышает потери в ней, вследствие чего амплитуда колебаний возрастает и достигает стационарного значения. В частности, если в систему поступает энергия больше, чем теряется в ней при сколь угодно малых амплитудах колебаний, то происходит самовозбуждение колебаний. Наоборот, при амплитудах, превышающих стационарное значение, потери энергии в системе обычно превышают поступление энергии из источника, вследствие чего амплитуда колебаний уменьшается и также достигает стационарного значения. Т. о., отклонения амплитуды А. в ту или другую сторону от стационарного значения затухают, и А. в этих случаях устойчивы.
Однако в некоторых случаях отклонение амплитуды колебаний от стационарного значения и нарушение компенсации потерь энергии в системе приводят к дальнейшему росту отклонений амплитуды от стационарного значения. Это будет иметь место, если при уменьшении амплитуды потери начинают преобладать над поступлением энергии или, наоборот, при увеличении амплитуды поступление энергии начинает преобладать над потерями. В этом случае А. неустойчивы, и, вследствие наличия во всякой реальной системе неизбежных возмущений и толчков, такие А. длительное время существовать не могут.
Форма А. может быть различной. Если добротность колебательной системы велика, т. е. потери энергии в колебательной системе относительно малы, то для поддержания А. в систему за период должно поступать количество энергии, очень малое по сравнению с полной энергией колебательной системы. При этом характер происходящих процессов почти не изменяется по сравнению с тем, как они протекали бы в системе без поступления энергии. В этом случае период и форма А. будут очень близки к периоду и форме собственных колебаний колебательной системы; если собственные колебания в системе по форме близки к гармоническим, то А. также близки к гармоническим.
В систему с малой добротностью для поддержания А. должна поступать энергия, уже не малая по сравнению с энергией системы, что может существенно изменить характер происходящих в ней процессов; в частности, форма А. может значительно отличаться от синусоидальной. Если за период А. рассеивается вся накопленная в системе энергия (т. е. система уже не колебательная, а апериодическая), то А. могут очень сильно отличаться по форме от синусоидальных, т. е. превратиться в т. н. релаксационные колебания.
ПАРАМЕТРИЧЕСКИЙ
РЕЗОНАНС
- явление раскачки колебаний при периодич.
изменении параметров тех элементов
колебат. системы, в к-рых сосредоточивается
энергия колебаний (реактивные или
энергоёмкие параметры). П. р. возможен
в колебат. системах разл. физ. природы.
Напр., в электрич. колебательном
контуре
реактивными параметрами являются
ёмкость С
и индуктивность L,
в к-рых запасены электрич. энергия Wэ
= q2/2C
и магн. энергия Wм
= LI2/2
(где q
- заряд на обкладках конденсатора, I
- ток в катушке индуктивности).
Собств. колебания в контуре без потерь
с постоянными С
и L
происходят с частотой![]() = 1/LC.
При этом полная энергия W
= Wэ
+ Wм,
запасённая в контуре, остаётся неизменной,
происходит лишь её периодич. трансформация
из электрической в магнитную и обратно
с частотой
= 1/LC.
При этом полная энергия W
= Wэ
+ Wм,
запасённая в контуре, остаётся неизменной,
происходит лишь её периодич. трансформация
из электрической в магнитную и обратно
с частотой![]() Изменение параметров С
и L,
сопровождающееся работой внеш. сил
(накачка), приводит к изменению полной
энергии системы. Если ёмкость С
изменить скачком за время, малое по
сравнению с периодом собств. колебаний
Изменение параметров С
и L,
сопровождающееся работой внеш. сил
(накачка), приводит к изменению полной
энергии системы. Если ёмкость С
изменить скачком за время, малое по
сравнению с периодом собств. колебаний![]() (рис. 1,а),
то заряд скачком измениться не может
(поскольку сила тока I
остаётся конечной величиной, рис. 1, б).
В результате напряжение
на ёмкости U
= q/C (рис.
1,в)
и электрич. энергия W, изменяются обратно
пропорц. С,
причём совершаемая при этом работа
пропорц. q2.
Если изменять ёмкость С
периодически в такт изменениям Wэ,
(обусловленным собств. колебаниями),
уменьшая её в моменты, когда q2
и Wэ
максимальны, и увеличивая, когда эти
величины равны нулю (рис. 1), то в ср. за
период над системой совершается положит.
работа и, следовательно, полная энергия
и амплитуда колебаний будут монотонно
нарастать.
(рис. 1,а),
то заряд скачком измениться не может
(поскольку сила тока I
остаётся конечной величиной, рис. 1, б).
В результате напряжение
на ёмкости U
= q/C (рис.
1,в)
и электрич. энергия W, изменяются обратно
пропорц. С,
причём совершаемая при этом работа
пропорц. q2.
Если изменять ёмкость С
периодически в такт изменениям Wэ,
(обусловленным собств. колебаниями),
уменьшая её в моменты, когда q2
и Wэ
максимальны, и увеличивая, когда эти
величины равны нулю (рис. 1), то в ср. за
период над системой совершается положит.
работа и, следовательно, полная энергия
и амплитуда колебаний будут монотонно
нарастать.
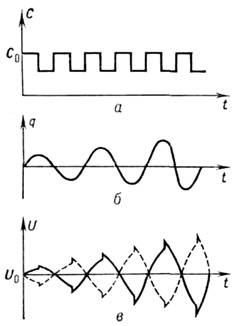
Рис. I. Связь между изменениями ёмкости С конденсатора (а), заряда q на его обкладках (б) и напряжения U (в)при параметрическом резонансе в колебательном контуре.
П. р. наиб. эффективно проявляется при изменении параметров колебат. системы с периодом Тн, кратным полупериоду собств. колебаний Т0:
![]()
где п
- целое число,![]() - частота накачки. Математически свободные
колебания
в таких системах описываются дифференц.
ур-ниями с переменными коэф. Напр., в
случае колебат. контура с перем. ёмкостью
C(t)(в
отсутствие омического сопротивления)
ур-ние относительно заряда q(l)имеет
вид
- частота накачки. Математически свободные
колебания
в таких системах описываются дифференц.
ур-ниями с переменными коэф. Напр., в
случае колебат. контура с перем. ёмкостью
C(t)(в
отсутствие омического сопротивления)
ур-ние относительно заряда q(l)имеет
вид
![]()
(ур-ние Xилла). Согласно Флоке теореме, общее решение (2) можно записать в виде
![]()
где С1,2
- произвольные коэф., определяемые нач.
условиями,![]() - периодич. ф-ция с периодом Тн
- периодич. ф-ция с периодом Тн![]() - коэф., зависящий от параметров системы.
При выполнении условия (1)
- коэф., зависящий от параметров системы.
При выполнении условия (1)![]() и один из членов (3) даёт нарастающие во
времени колебания. Наиб. быстрая раскачка
имеет место при п
= 1, когда
частота накачки
и один из членов (3) даёт нарастающие во
времени колебания. Наиб. быстрая раскачка
имеет место при п
= 1, когда
частота накачки![]() равна частоте колебаний величин Wо
и WM
в
системе
равна частоте колебаний величин Wо
и WM
в
системе![]() Нарастание колебаний возможно не только
при точном выполнении соотношений (1),
но и в нек-рых конечных интервалах
значений
Нарастание колебаний возможно не только
при точном выполнении соотношений (1),
но и в нек-рых конечных интервалах
значений![]() вблизи
вблизи![]() (в зонах неустойчивости), ширина зон тем
больше, чем сильнее изменяются параметры
С
и L.
Изменение параметра, напр. ёмкости С,
характеризуют величиной
(в зонах неустойчивости), ширина зон тем
больше, чем сильнее изменяются параметры
С
и L.
Изменение параметра, напр. ёмкости С,
характеризуют величиной
т = (Смакс - С мин)/(Cмакс + Cмин),
наз. глубиной
изменения параметра. В частном случае
синусоидального изменения![]()
[ур-ние (2) при этом
наз. ур-нием Матьё] в осн. зоне (п
= 1) при т![]() 1 инкремент
1 инкремент![]() равен
равен
![]()
так что в середине
зоны![]() во второй зоне (п
=2)
во второй зоне (п
=2)![]() ~ m2,
в третьей
~ m2,
в третьей![]() ~ т3
и т. д.
П. р. приводит к неустойчивости
колебат. системы, т. е. к нарастанию малых
нач. возмущений, напр. неизбежных во
всякой системе флуктуаций, среди к-рых
всегда найдётся составляющая с подходящей
фазой по отношению к фазе изменения
параметров. В отсутствие потерь энергии
параметрич. неустойчивость наступает
при сколь угодно малой глубине изменения
параметров. Если же в системе имеются
потери (напр., в контуре присутствует
сопротивление R),
то неустойчивость возникает только при
достаточно больших изменениях С
или L,
когда параметрич. накачка энергии
превосходит потери. Зоны неустойчивости
при этом соответственно уменьшаются
или даже исчезают совсем (на рис. 2)
уменьшать l
в нижнем и увеличивать в крайних
положениях [при этом снова выполняется
соотношение (1)], то работа внеш. силы,
совершаемая в ср. за период, оказывается
положительной и колебания могут
раскачиваться. На П. р. основано
самораскачивание на качелях, когда эфф.
длина маятника периодически изменяется
при приседаниях и вставаниях качающегося.
П. р. учитывается в небесной механике
при расчёте возмущений планетных орбит,
вызванных влиянием др. планет.
В
колебат. системах с неск. степенями
свободы (напр., в системе из двух связанных
контуров, маятников и др.) возможны
нормальные колебания (моды) с разя,
частотами
~ т3
и т. д.
П. р. приводит к неустойчивости
колебат. системы, т. е. к нарастанию малых
нач. возмущений, напр. неизбежных во
всякой системе флуктуаций, среди к-рых
всегда найдётся составляющая с подходящей
фазой по отношению к фазе изменения
параметров. В отсутствие потерь энергии
параметрич. неустойчивость наступает
при сколь угодно малой глубине изменения
параметров. Если же в системе имеются
потери (напр., в контуре присутствует
сопротивление R),
то неустойчивость возникает только при
достаточно больших изменениях С
или L,
когда параметрич. накачка энергии
превосходит потери. Зоны неустойчивости
при этом соответственно уменьшаются
или даже исчезают совсем (на рис. 2)
уменьшать l
в нижнем и увеличивать в крайних
положениях [при этом снова выполняется
соотношение (1)], то работа внеш. силы,
совершаемая в ср. за период, оказывается
положительной и колебания могут
раскачиваться. На П. р. основано
самораскачивание на качелях, когда эфф.
длина маятника периодически изменяется
при приседаниях и вставаниях качающегося.
П. р. учитывается в небесной механике
при расчёте возмущений планетных орбит,
вызванных влиянием др. планет.
В
колебат. системах с неск. степенями
свободы (напр., в системе из двух связанных
контуров, маятников и др.) возможны
нормальные колебания (моды) с разя,
частотами![]() ,
,![]() Поэтому колебания энергии, запасённой
в к--л. реактивном элементе, содержат не
только составляющие с частотами
Поэтому колебания энергии, запасённой
в к--л. реактивном элементе, содержат не
только составляющие с частотами![]() .
.![]() ,
но и с частотами, равными суммам и
разностям разл. нормальных частот.
Соответственно нарастание колебаний
здесь возможно как при выполнении
условия (1) для любой из нормальных
частот, так и, напр., при изменении
параметра с суммарной частотой:
,
но и с частотами, равными суммам и
разностям разл. нормальных частот.
Соответственно нарастание колебаний
здесь возможно как при выполнении
условия (1) для любой из нормальных
частот, так и, напр., при изменении
параметра с суммарной частотой:
![]()
П. р. приводит к
самовозбуждению обоих нормальных
колебаний с определ. соотношением фаз.
Резонансная связь мод возможна также
при![]() однако при этом вместо самовозбуждения
происходит лишь периодич. перекачка
энергии между модами. Соотношение (2)
выражает закон сохранения энергии при
распаде кванта "накачки" с энергией
однако при этом вместо самовозбуждения
происходит лишь периодич. перекачка
энергии между модами. Соотношение (2)
выражает закон сохранения энергии при
распаде кванта "накачки" с энергией![]() на два кванта:
на два кванта:![]() и
и![]() . Отсюда следует также, что мощность Рн,
поступающая в колебат. систему на
частоте
. Отсюда следует также, что мощность Рн,
поступающая в колебат. систему на
частоте![]() ,
и мощности Р1,
Р2,
потребляемые на частотах
,
и мощности Р1,
Р2,
потребляемые на частотах![]() и
и![]() пропорц. соответствующим частотам
(частный случай т. н. соотношений Мэнли
- Роу):
пропорц. соответствующим частотам
(частный случай т. н. соотношений Мэнли
- Роу):
![]()
В колебат. системах с распределёнными параметрами, обладающих бесконечным числом степеней свободы, также возможно возбуждение нормальных колебаний в результате П. р. Классич. пример - опыт Мельде (1859), в к-ром наблюдалось возбуждение поперечных колебаний (стоячих волн) в струне, прикреплённой одним концом к ножке камертона, колебания к-рого периодически меняют натяжение струны (рис. 4) с частотой, вдвое больше частоты собств. поперечных колебаний. П. р. может приводить к раскачке изгибных колебаний вращающихся валов. Др. пример - опыт Фарадея (1831), в к-ром вертикальные колебания сосуда с водой приводит к возбуждению стоячей поверхностной воды с удвоенным периодом.

Рис. 4. Параметрическое побуждение колебаний струны.
Существ. особенность
П. р. в волновых системах состоит в том,
что его эффективность зависит от
соотношения между законом изменения
параметров системы в пространстве и
пространственной структурой воли.
Напр., если накачка, изменяющая параметры
среды, представляет собой бегущую волну
с частотой![]() и волновым
вектором
kH,
то возбуждение пары нормальных волн с
частотами
и волновым
вектором
kH,
то возбуждение пары нормальных волн с
частотами![]() ,
,![]() и волновыми векторами k1,
k2
осуществляется, если выполняются условия
П. р. как во времени, так и в пространстве:
и волновыми векторами k1,
k2
осуществляется, если выполняются условия
П. р. как во времени, так и в пространстве:
![]() kH
= k+ k2.
(4)
kH
= k+ k2.
(4)
В предельном случае
бесконечно большой фазовой скорости
волны накачки![]() (kн
(kн![]() 0
при конечном
0
при конечном![]() ) условия (4) дают k2
) условия (4) дают k2![]() - k1,
и в простейшем случае
- k1,
и в простейшем случае![]() т. е. нарастать может стоячая
волна
на половинной частоте. В другом предельном
случае (
т. е. нарастать может стоячая
волна
на половинной частоте. В другом предельном
случае (![]() 0 при конечном kн,
0 при конечном kн,![]()
![]() )
равенства (4) сводятся к условию
резонансного (брэггов-ского) отражения
от неподвижной периодич. неоднородности
среды; здесь полная энергия сигнала
остаётся постоянной, а происходит его
отражение (непропускание) периодич.
структурой.
На квантовом языке
условия (4) означают, что при распаде
кванта накачки сохраняются как энергия,
так и импульс
)
равенства (4) сводятся к условию
резонансного (брэггов-ского) отражения
от неподвижной периодич. неоднородности
среды; здесь полная энергия сигнала
остаётся постоянной, а происходит его
отражение (непропускание) периодич.
структурой.
На квантовом языке
условия (4) означают, что при распаде
кванта накачки сохраняются как энергия,
так и импульс![]() .
Нарастание амплитуд волн во времени и
в пространстве (распадная неустойчивость)
также ограничивается нелинейными
эффектами: если значит. часть энергии
накачки израсходована на возбуждение
этих волн, то возможен обратный процесс
- рост энергии накачки за счёт ослабления
волн на частотах
.
Нарастание амплитуд волн во времени и
в пространстве (распадная неустойчивость)
также ограничивается нелинейными
эффектами: если значит. часть энергии
накачки израсходована на возбуждение
этих волн, то возможен обратный процесс
- рост энергии накачки за счёт ослабления
волн на частотах![]() ,
,![]() ; в среде без потерь такой обмен энергией
происходит периодически.
Возможны
также многоволновые процессы, когда во
взаимодействии участвует большее число
волн.
Параметрич. и нелинейные
резонансные взаимодействия волн
характерны, напр., для разл. типов волн
в плазме,
мощных световых волн (см. Параметрический
генератор света
),волн в электронных пучках и др. волновых
процессов.
; в среде без потерь такой обмен энергией
происходит периодически.
Возможны
также многоволновые процессы, когда во
взаимодействии участвует большее число
волн.
Параметрич. и нелинейные
резонансные взаимодействия волн
характерны, напр., для разл. типов волн
в плазме,
мощных световых волн (см. Параметрический
генератор света
),волн в электронных пучках и др. волновых
процессов.
Дифференциальное волновое уравнение.
Дифференциальное уравнение с частными производными, описывающее процесс распространения возмущений в некоторой среде. В случае малых возмущений и однородной изотропной среды В. у. имеет вид:
![]()
где х, у, z - пространственные переменные, t - время, u = u (х, у, z) - искомая функция, характеризующая возмущение в точке (х, у, z) в момент t, а - скорость распространения возмущения. В. у. является одним из основных уравнений математической физики и широко используется в приложениях. Если u зависит только от двух (одной) пространственных переменных, то В. у. упрощается и называется двумерным (одномерным). В. у. допускает решение в виде "расходящейся сферической волны":
u = f (t - r/a)/r,
где f - произвольная функция, a
![]()
Особый интерес представляет так называемое элементарное решение (элементарная волна):
u = δ (t - r/a)/r
(где δ - Дельта-функция), дающее процесс распространения возмущения, произведённого мгновенным точечным источником (действовавшим в начале координат при t = 0). Образно говоря, элементарная волна представляет собой "бесконечный всплеск" на окружности r = at, удаляющийся от начала координат со скоростью а с постепенным уменьшением интенсивности. При помощи наложения элементарных волн можно описать процесс распространения произвольного возмущения.
Малые колебания струны описываются одномерным В. у.:
![]()
Что такое волна. Бегущая волна. Формула волны, распространяющейся вдоль оси Ох. Стоячая волна. Формула монохроматической волны. Длина волны и волновое число. Фронт, волновые поверхности, лучи.
Сферическая волна. Сходящиеся и расходящиеся решения.
СФЕРИЧЕСКАЯ ВОЛНА - волна, радиально расходящаяся от нек-рой точки (источника) или сходящаяся к ней (к стоку) и имеющая сферич. волновые фронты (поверхности равных фаз). Простейшим примером является сферически симметричная скалярная волна вида
![]()
расходящаяся от центр. точки r = 0 (знак " -") или сходящаяся к ней (знак "+") со скоростью с. Такая волна удовлетворяет волновому уравнению и описывает многие физ. процессы в линейных средах без дисперсии и без потерь. Суперпозиция сходящейся и расходящейся волн (в частности, стоячая С. в.) также является решением волнового ур-ния.
Ф-ция f в общем случае произвольна; важный частный случай - гармоническая С. в.: f=A expi(wt + kr); в такой волне А/r - амплитуда, а wt + kr = Ф - фаза (w - круговая частота, k - волновое число).
Если величина u(r, t)описывает физ. поле (напр., возмущение давления в звуковой волне, скалярный потенциал в эл--магн. волне и др.), то плотность потока энергии поля, уносимой от источника или приносимой к нему, пропорц. |u(r, t)|2, и, следовательно, общий поток энергии через сферу любого радиуса r, пропорц. 4pr2|и|2, сохраняется неизменным. Это является следствием закона сохранения энергии.
При наличии поглощения в среде энергия С. в. убывает в направлении её распространения. Для гармонии. С. в. поглощение может быть учтено заменой k на k' + k'', где k'' - мнимая часть волнового числа. Это означает, что амплитуда волны затухает по экспоненте:
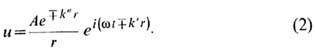
Существуют и несимметричные С. в., амплитуды к-рых зависят от полярной q и азимутальной j угл. координат, но фазовые фронты по-прежнему остаются сферическими:
![]()
где U(r, t)отвечает симметричной С. в., напр. в форме (1) или (2), a D(q, j) описывает угл. зависимость поля (эту ф-цию можно представить в виде суперпозиции т. н. сферич. гармоник). В однородных изотропных средах волновое поле на больших расстояниях от центра почти всегда имеет вид (3). Подбором D можно концентрировать поле около заданных направлений, поэтому ф-ция D(q, j) наз. диаграммой направленности излучения источника.
Волновой пакет. Принцип неопределенности. Толщина луча.
ВОЛНОВОЙ
ПАКЕТ
- волновое образование из колебаний
произвольной природы, представляющее
собой суперпозицию (наложение) плоских
монохроматич. волн с близкими значениями
частот
![]() и
волновых векторов (k).
B случае одного пространственного
измерения (х)и
скалярного комплексного волнового поля
В. п.
и
волновых векторов (k).
B случае одного пространственного
измерения (х)и
скалярного комплексного волнового поля
В. п.
![]() можно
представить в виде интеграла Фурье:
можно
представить в виде интеграла Фурье:
![]()
где
g
(k)заметно
отлично от нуля лишь для значений k,
лежащих внутри интервала
![]() вблизи
нек-рого k=k0.
В отличие от плоской монохроматич.
волны, существующей во всем пространстве,
В. п. занимает конечную часть пространства,
т. к. из (1) следует:
вблизи
нек-рого k=k0.
В отличие от плоской монохроматич.
волны, существующей во всем пространстве,
В. п. занимает конечную часть пространства,
т. к. из (1) следует:
![]()
Разброс
![]() по
координатам ф-ции
по
координатам ф-ции
![]() (ширина
пакета) скоррелирован с разбросом Dk
ф-ции g(k)по
волновым числам k:
(ширина
пакета) скоррелирован с разбросом Dk
ф-ции g(k)по
волновым числам k:
![]()
Под
разбросом (шириной) величины
![]() понимается
среднеквадратичное отклонение
понимается
среднеквадратичное отклонение![]() . Эволюция В. п. (1) предопределена, если
известны g
(k)и закон
дисперсии волн-связь
. Эволюция В. п. (1) предопределена, если
известны g
(k)и закон
дисперсии волн-связь
![]() и
k:
и
k:
![]()
Если
эта связь линейна,
![]() ,
где с=const (как в случае световых волн в
пустоте), то
,
где с=const (как в случае световых волн в
пустоте), то

т. е. В. п. распространяется со скоростью с без изменения своей формы.
В
общем случае произвольной связи
![]() и
k
зависимость
и
k
зависимость
![]() от
х
и t
имеет более сложный вид, и характер
распространения В. п. может быть описан
следующим усредненным (интегральным)
соотношением:
от
х
и t
имеет более сложный вид, и характер
распространения В. п. может быть описан
следующим усредненным (интегральным)
соотношением:
![]()
описывающим
равномерное движение центра тяжести
В. п. с групповой
скоростью
![]() ,
и равенством
,
и равенством
![]()
характеризующим
расширение со временем ("расплывание")
В. п., где
![]() -
среднеквадратичный разброс величины
-
среднеквадратичный разброс величины
![]()
В
квантовой
механике
для волны,
де Бройля
частицы![]() (где р,
т - импульс
и масса частицы), т. е. совпадает со ср.
значением классич. скорости частицы, а
(где р,
т - импульс
и масса частицы), т. е. совпадает со ср.
значением классич. скорости частицы, а
![]() ,
где
,
где
![]() -
среднеквадратичный разброс по импульсам
в В. п. Соотношения (6), (7) и (4) сыграли
важную роль в создании осн. квантовых
представлений. Тот факт, что центр масс
локализованного в пространстве В. п.,
составленного из волн
де Бройля,
перемещается со скоростью классич.
частицы, явился иллюстрацией предельного
перехода квантовомеханич. законов
движения к законам движения классич.
частицы по классич. траектории. Аналогично
факт расплывания В. п. со временем
способствовал принятию статистич.
интерпретации квантовой механики
(поскольку из него следовало, что квадрат
модуля волновой
функции
нельзя рассматривать как плотность
частицы). Учитывая, что в квантовой
теории
-
среднеквадратичный разброс по импульсам
в В. п. Соотношения (6), (7) и (4) сыграли
важную роль в создании осн. квантовых
представлений. Тот факт, что центр масс
локализованного в пространстве В. п.,
составленного из волн
де Бройля,
перемещается со скоростью классич.
частицы, явился иллюстрацией предельного
перехода квантовомеханич. законов
движения к законам движения классич.
частицы по классич. траектории. Аналогично
факт расплывания В. п. со временем
способствовал принятию статистич.
интерпретации квантовой механики
(поскольку из него следовало, что квадрат
модуля волновой
функции
нельзя рассматривать как плотность
частицы). Учитывая, что в квантовой
теории
![]() ,
из (3) непосредственно получается
неопределенностей
соотношение
для координаты и импульса:
,
из (3) непосредственно получается
неопределенностей
соотношение
для координаты и импульса:
![]()
Для движения частицы во внеш. поле в случае, когда спектр её энергии дискретен, также может быть рассмотрен В. п., представляющий собой суперпозицию состояний с разл. значениями энергии. Центр масс такого В. п. тоже движется по классяч. траектории, при этом для нек-рых потенциалов поля (типа потенциала поля осциллятора) существуют нерасплывающиеся В. п. (см. Когерентное состояние).
При
использовании соотношений (6), (7) для
распространения света в среде следует
иметь в виду, что они получены в
предположении вещественности
![]() ,
т. е. в пренебрежении эффектами диссипации.
Эти соотношения могут оказаться
неправильными при их формальном
использовании в случае В. п. с частотами,
лежащими вблизи области т. н. аномальной
дисперсии данной среды, где диссипац.
эффектами пренебрегать нельзя. В этой
области частот понятие групповой
скорости теряет смысл, поскольку при
движении В. п. будет происходить его
сильное экспоненциальное затухание,
как это следует из выражения (1).
,
т. е. в пренебрежении эффектами диссипации.
Эти соотношения могут оказаться
неправильными при их формальном
использовании в случае В. п. с частотами,
лежащими вблизи области т. н. аномальной
дисперсии данной среды, где диссипац.
эффектами пренебрегать нельзя. В этой
области частот понятие групповой
скорости теряет смысл, поскольку при
движении В. п. будет происходить его
сильное экспоненциальное затухание,
как это следует из выражения (1).
«Принцип неопределенности» - один из базовых принципов квантовой механики. Согласно ему некоторые пары физических величин, например, координаты и скорость или время и энергия, не могут одновременно иметь полностью определенные значения. Так чем точнее известна скорость частицы, тем больше «размазано» ее местоположение, или чем меньше время жизни возбужденного состояния атома, тем больше его ширина (разброс энергий). Считается, что неопределенность выражается в невозможности точного измерения значений пар этих величин.
В полевой физике тоже возникают похожие соотношения, только они приобретают диаметрально противоположный смысл и связаны с неустойчивостью квантовых процессов. Так в классической физике большинство функций y = f(x), которые описывают движение, является непрерывными: – сколько угодно малому изменению аргумента ∆x соответствует сколь угодно малое изменение значения функции ∆y:
![]()
Например, за малый промежуток времени ∆t энергия классической системы изменяется на малую величину ∆E.
В квантовых условиях все происходит наоборот. Квантовые системы обычно имеют дискретные характеристики, а значит, сколь угодно малое изменение одного из параметров уже не может привести к сколь угодно малому изменению другого параметра. К этому и приводит полевая физика. Так в отличие от классического случая сколь угодно малое изменение характерного времени системы (периода или собственной частоты) оказывается возможным только при сколько угодно большом изменении энергии системы. В результате переход с одной собственной частоты на другую происходит скачком, при этом также скачком изменяется и величина энергии системы. Причем чем меньше оказывается при таком скачкообразном переходе изменение собственного времени системы ∆t, тем большее изменение величины энергии ∆E ему соответствует и наоборот.
Другими словами, в квантовых условиях между такими парами величин, как характерное время и энергия, или положение и импульс, выполняется обратная связь малых приращений, нежели для дифференцируемых функций. Для этих зависимостей сколь угодно малое изменение аргумента соответствует сколь угодно большому изменению значений функции и наоборот. То есть малые приращения оказываются не пропорциональными друг другу, а обратно пропорциональными:
![]()
Эту связь можно выразить и по-другому, записав, что произведение двух приращений должно иметь порядок некой константы h (есть речь идет не о безразмерных, а о реальных физических величинах)
![]()
Поперечные волны на натянутой струне. Стоячие волны как собственные колебания струны.
Продольные и поперечные упругие волны.
В физике мы имеем дело с волнами различной природы: механическими, электромагнитными и т.д. Несмотря на отличия, эти волны имеют много общих черт. Волны, рассматриваемый параметр которых (смещение молекул, механическое напряжение, и т.д.) изменяется периодически вдоль оси распространения, называются продольными волнами. Если колебания происходят перпендикулярно оси распространения волны (как у электромагнитных волн, например), то такие волны называются поперечными.
Е
 сли
взаимосвязь между частицами среды
осуществляется силами упругости,
возникающими вследствие деформации
среды при передаче колебаний от одних
частиц к другим, то волны называются
упругими. К ним относятся звуковые,
ультразвуковые, сейсмические и др.
волны. На первой анимации изображён
процесс распространения продольной
упругой волны в решётке, состоящей из
шариков, соединённых упругими пружинками.
Каждый шарик колеблется по гармоническому
закону в продольном направлении,
совпадающем с направлением распространения
волны. Амплитуда каждого шарика одинакова
и равна A,
а фаза колебаний линейно растёт с
увеличением номера шарика на Dj т.е.
сли
взаимосвязь между частицами среды
осуществляется силами упругости,
возникающими вследствие деформации
среды при передаче колебаний от одних
частиц к другим, то волны называются
упругими. К ним относятся звуковые,
ультразвуковые, сейсмические и др.
волны. На первой анимации изображён
процесс распространения продольной
упругой волны в решётке, состоящей из
шариков, соединённых упругими пружинками.
Каждый шарик колеблется по гармоническому
закону в продольном направлении,
совпадающем с направлением распространения
волны. Амплитуда каждого шарика одинакова
и равна A,
а фаза колебаний линейно растёт с
увеличением номера шарика на Dj т.е.
x0=Asin(wt); x1=Asin(wt+Dj); x2=Asin(wt+2Dj); x3=Asin(wt+3Dj); и т.д.
где w -частота волны, t - время, Dj - изменение фазы от шарика к шарику
В
 поперечной волне колебания происходят
в направлении, перпендикулярном
направлению распространения волны. Как
и в случае продольных волн амплитуды
колебаний всех шариков одинаковы, а
фаза линейно изменяется от шарика к
шарику
поперечной волне колебания происходят
в направлении, перпендикулярном
направлению распространения волны. Как
и в случае продольных волн амплитуды
колебаний всех шариков одинаковы, а
фаза линейно изменяется от шарика к
шарику
y0=Bsin(wt); y1=Bsin(wt+Dj); y2=Bsin(wt+2Dj); y3=Bsin(wt+3Dj); и т.д.
В общем виде уравнение распространения волны может быть записано в виде: z = Acos(wt - kx), где z - координата, по которой происходит движение частиц, x - координата оси, вдоль которой распространяется волна, k - волновое число, равное w / v, v - скорость распространения волны. Зная частоту волны и скорость её распространения, мы можем найти сдвиг фаз между соседними шариками (частицами): Dj = (w / v)a, где a - расстояние между шариками в решётке.
Н
 а
следующей анимации изображено наложение
продольной и поперечной волн равной
амплитуды, сдвинутых по фазе на 90
градусов. В результате каждая масса
совершает круговые движения. Уравнение
движения каждого шарика может быть
описано уравнением:
а
следующей анимации изображено наложение
продольной и поперечной волн равной
амплитуды, сдвинутых по фазе на 90
градусов. В результате каждая масса
совершает круговые движения. Уравнение
движения каждого шарика может быть
описано уравнением:
x=Acos(wt+j0); y=Asin(wt+j0)
У
 волн, наблюдаемых на поверхности
жидкости, так называемых поверхностных
волн, взаимосвязь между соседними
элементами поверхности жидкости при
передаче колебаний осуществляется не
силами упругости, а силами поверхностного
натяжения и тяжести. Колебания масс в
сетке моделируют движение молекул в
волне на поверхности жидкости. В случае
малой амплитуды волны каждая масса
движется по окружности, радиус которой
убывает с расстоянием от поверхности.
Массы внизу сетки находятся в покое.
волн, наблюдаемых на поверхности
жидкости, так называемых поверхностных
волн, взаимосвязь между соседними
элементами поверхности жидкости при
передаче колебаний осуществляется не
силами упругости, а силами поверхностного
натяжения и тяжести. Колебания масс в
сетке моделируют движение молекул в
волне на поверхности жидкости. В случае
малой амплитуды волны каждая масса
движется по окружности, радиус которой
убывает с расстоянием от поверхности.
Массы внизу сетки находятся в покое.
В
 олны
на поверхности жидкости не являются ни
продольными, ни поперечными. Как мы
можем видеть на анимации, красный шарик,
моделирующий молекулу поверхности
жидкости, движется по круговой траектории.
Таким образом, волна на поверхности
жидкости представляет собой суперпозицию
продольного и поперечного движения
молекул.
олны
на поверхности жидкости не являются ни
продольными, ни поперечными. Как мы
можем видеть на анимации, красный шарик,
моделирующий молекулу поверхности
жидкости, движется по круговой траектории.
Таким образом, волна на поверхности
жидкости представляет собой суперпозицию
продольного и поперечного движения
молекул.
Плотность энергии упругой волны. Плотность импульса упругой волны (вектор Умова).
Электромагнитные волны. Перпендикулярность полей E и B. Плоская поляризованная электромагнитная волна. Линейная, круговая и эллиптическая поляризация.
 Шкала
электромагнитных волн
Шкала
электромагнитных волн
Шкала электромагнитных волн
Электромагнитные волны, электромагнитные колебания, распространяющиеся в пространстве с конечной скоростью. Существование Э. в. было предсказано М. Фарадеем в 1832. Дж. Максвелл в 1865 теоретически показал, что электромагнитные колебания не остаются локализованными в пространстве, а распространяются в вакууме со скоростью света с во все стороны от источника. Из того обстоятельства, что скорость распространения Э. в. в вакууме равна скорости света, Максвелл сделал вывод, что свет представляет собой Э. в. В 1888 максвелловская теория Э. в. получила подтверждение в опытах Г. Герца, что сыграло решающую роль для её утверждения.
Теория Максвелла позволила единым образом подойти к описанию радиоволн, света, рентгеновских лучей и гамма-излучения. Оказалось, что это не излучения различной природы, а Э. в. с различной длиной волны. Частота w колебаний электрического Е и магнитного Н полей связана с длиной волны l соотношением: l= 2pс/w. Радиоволны, рентгеновские лучи и g-излучение находят своё место в единой шкале Э. в. (рис.), причём между соседними диапазонами шкалы Э. в. нет резкой границы.
Особенности Э. в., законы их возбуждения и распространения описываются Максвелла уравнениями. Если в какой-то области пространства существуют электрические заряды е и токи I, то изменение их со временем t приводит к излучению Э. в. На скорость распространения Э. в. существенно влияет среда, в которой они распространяются. Э. в. могут испытывать преломление, в реальных средах имеет место дисперсия волн, вблизи неоднородностей наблюдаются дифракция волн, интерференция волн (прямой и отражённой), полное внутреннее отражение и другие явления, свойственные волнам любой природы. Пространств, распределение электромагнитных полей, временные зависимости E (t) и H (t), определяющие тип волн (плоские, сферические и др.), вид поляризации (см. Поляризация волн) и другие особенности Э. в. задаются, с одной стороны, характером источника излучения, и с другой — свойствами среды, в которой они распространяются. В случае однородной и изотропной среды, вдали от зарядов и токов, создающих электромагнитное поле, уравнения Максвелла, приводят к волновым уравнениям:
![]() ;
;
![]() ,
,
описывающим распространение плоских монохроматических Э. в.:
Е = E0 cos (kr — wt + j)
Н = H0 cos (kr — wt + j).
Здесь e — диэлектрическая проницаемость, mÑ — магнитная проницаемость среды, E0 и H0 — амплитуды колебаний электрических и магнитных полей, w — частота этих колебаний, j — произвольный сдвиг фазы, k — волновой вектор, r — радиус-вектор точки; Ñ2 — Лапласа оператор.
Если среда неоднородна или содержит поверхности, на которых изменяются её электрические либо магнитные свойства, или если в пространстве имеются проводники, то тип возбуждаемых и распространяющихся Э. в. может существенно отличаться от плоской линейно-поляризованной волны. Э. в. могут распространяться вдоль направляющих поверхностей (поверхностные волны), в передающих линиях и в полостях, образованных хорошо проводящими стенками.
Характер изменения во времени Е и Н определяется законом изменения тока I и зарядов e, возбуждающих Э. в. Однако форма волны в общем случае не следует I (t) или e (t). Она в точности повторяет форму тока только в случае, если и Э. в. распространяются в линейной среде (электрические и магнитные свойства которой не зависят от Е и Н). Простейший случай — возбуждение и распространение Э. в. в однородном изотропном пространстве с помощью диполя Герца (отрезка провода длиной l << l, по которому протекает ток I = I0 sin wt). На расстоянии от диполя много большем l образуется волновая зона (зона излучения), где распространяются сферические Э. в. Они поперечные и линейно поляризованы. В случае анизотропии среды могут возникнуть изменения поляризации (см. Излучение и приём радиоволн).
В изотропном
пространстве скорость распространения
гармонических Э. в., т. e. фазовая скорость
![]() .
При наличии дисперсии скорость переноса
энергии с
(групповая
скорость)
может отличаться от v.
Плотность потока энергии S, переносимой
Э. в., определяется Пойнтинга
вектором:
S = (с/4p) [ЕН].
Т.
к. в изотропной среде векторы Е
и Н и волновой
вектор образуют правовинтовую систему,
то S
совпадает с направлением распространения
Э. в. В анизотропной среде (в том числе
вблизи проводящих поверхностей) S
может не совпадать с направлением
распространения Э. в.
.
При наличии дисперсии скорость переноса
энергии с
(групповая
скорость)
может отличаться от v.
Плотность потока энергии S, переносимой
Э. в., определяется Пойнтинга
вектором:
S = (с/4p) [ЕН].
Т.
к. в изотропной среде векторы Е
и Н и волновой
вектор образуют правовинтовую систему,
то S
совпадает с направлением распространения
Э. в. В анизотропной среде (в том числе
вблизи проводящих поверхностей) S
может не совпадать с направлением
распространения Э. в.
Появление квантовых генераторов, в частности лазеров, позволило достичь напряжённости электрического поля в Э. в., сравнимых с внутриатомными полями. Это привело к развитию нелинейной теории Э. в. При распространении Э. в. в нелинейной среде (e и m зависят от Е и Н) её форма изменяется. Если дисперсия мала, то по мере распространения Э. в. они обогащаются т. н. высшими гармониками и их форма постепенно искажается. Например, после прохождения синусоидальной Э. в. характерного пути (величина которого определяется степенью нелинейности среды) может сформироваться ударная волна, характеризующаяся резкими изменениями Е и Н (разрывы) с их последующим плавным возвращением к первоначальным величинам. Ударная Э. в. далее распространяется без существ, изменений формы; сглаживание резких изменений обусловлено главным образом затуханием. Большинство нелинейных сред, в которых Э. в. распространяются без сильного поглощения, обладает значительной дисперсией, препятствующей образованию ударных Э. в. Поэтому образование ударных волн возможно лишь в диапазоне l от нескольких см до длинных волн. При наличии дисперсии в нелинейной среде возникающие высшие гармоники распространяются с различной скоростью и существенного искажения формы исходной волны не происходит. Образование интенсивных гармоник и взаимодействие их с исходной волной может иметь место лишь при специально подобранных законах дисперсии (см. Нелинейная оптика, Параметрические генераторы света).
Э. в. различных диапазонов l характеризуются различными способами возбуждения и регистрации, по-разному взаимодействуют с веществом и т. п. Процессы излучения и поглощения Э. в. от самых длинных волн до инфракрасного излучения достаточно полно описываются соотношениями электродинамики. На более высоких частотах доминируют процессы, имеющие существенно квантовую природу, а в оптическом диапазоне и тем более в диапазонах рентгеновских и g-лучей излучение и поглощение Э. в. могут быть описаны только на основе представлений о дискретности этих процессов.
Квантовая
теория поля
внесла существенные дополнения и в само
представление об Э. в. Во многих случаях
электромагнитное излучение ведёт себя
не как набор монохроматических Э. в. с
частотой w и волновым вектором k,
а как поток квазичастиц — фотонов
с энергией
![]() и
импульсом
и
импульсом
![]() (
(
![]() —
Планка
постоянная).
Волновые свойства проявляются, например,
в явлениях дифракции и интерференции,
корпускулярные — в фотоэффекте
и Комптона
эффекте.
—
Планка
постоянная).
Волновые свойства проявляются, например,
в явлениях дифракции и интерференции,
корпускулярные — в фотоэффекте
и Комптона
эффекте.
Поляризация электромагнитных волн (ПЭВ) — одно из фундаментальных свойств оптического излучения (света), состоящее в искажении различных направлений в плоскости, перпендикулярной световому лучу (направлению распространения световой волны).[1]
ПЭВ — явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H.
Когерентное электромагнитное излучение может иметь:
 Эллипс
поляризации
Эллипс
поляризации
![]() Добавил
Moisey
Добавил
Moisey
Линейную поляризацию — в направлении, перпендикулярном направлению распространения волны;
Круговую поляризацию — правую либо левую, в зависимости от направления вращения вектора индукции;
Эллиптическую поляризацию — случай, промежуточный между круговой и линейными поляризациями.
Некогерентное излучение может не быть поляризованным, может быть полностью или частично поляризованным любым из указанных способов. В таком случае понятие поляризации понимается статистически.
При теоретическом рассмотрении поляризации волна полагается распространяющейся горизонтально. В этом случае можно рассматривать вертикальную и горизонтальную линейные поляризациии волны.



Линейная поляризацияКруговая поляризацияЭллиптическая поляризация
Для понимания явления поляризации света имело её проявление в эффекте интерференции света. Именно тот факт, что когда два световых луча, линейно поляризованных под прямым углом друг к другу, при простейшей постановке опыта не интерферируют, явился решающим доказательством поперечности световых волн (Френель, Араго, Т. Юнг, 1816—19). Поляризация света нашла естественное объяснение в электромагнитной теории света Дж. К. Максвелла (1865—73).
Поперечность световых волн (как и любых др. электромагнитных волн) выражается в том, что колеблющиеся в них векторы напряжённости электрического поля интерференции Е и напряжённости магнитного поля Н перпендикулярны направлению распространения волны. Е и Н выделяют (отсюда указанное выше неравноправие) определённые направления в пространстве, занятом волной. При этом Е и Н почти всегда взаимно перпендикулярны, поэтому для полного описания состояния поляризация света требуется знать поведение лишь одного из них. Обычно для этой цели выбирают вектор Е.
Плотность энергии волны ЭМ волны.
Вектор Умова-Пойнтинга.
Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
![]() (в
системе СГС),
(в
системе СГС),
![]() (в
системе СИ),
(в
системе СИ),
где E и H — векторы напряжённости электрического и магнитного полей соответственно.
![]() (в
комплексной форме),
(в
комплексной форме),
где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно.
Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.
Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны, то вектор S непрерывен на границе двух сред.
Затухающая волна. Затухание во времени и в пространстве.
Фазовая и групповая скорости волны. Связь с дисперсией. Скорость передачи энергии и информации
Фазовая скорость, это скорость одной волны груповая скорость, это скорость пакета волн разной частоты скорость дневного света не может быть фазовой т.к. состоит иэ группы волн разной частоты т.е. она груповая луч лазера является монохромным, и поэтому его скорость фазовая. здесь волна характеризуется груповой скоростью:
|
а здесь фазовой:
|
Закон преломления Снелла. Полное внутреннее отражение.
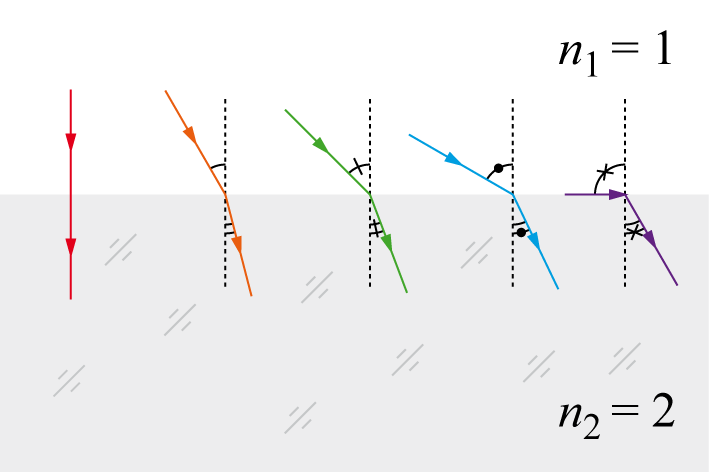
Закон преломления света для лучей на границе сред с показателями преломления n1 = 1 и n2 = 2
Закон Снелла (Снеллиуса) преломления света описывает преломление света на границе двух сред. Также применим и для описания преломления волн другой природы, например звуковых. Закон был открыт в начале XVII века голландским математиком Виллебрордом Снеллом, известным также под латинизированным именем Снеллиус. Закон преломления света утверждает: угол падения света на поверхность связан с углом преломления соотношением:
n1·sin α1 = n2·sin α2
Здесь: n1 — показатель преломления среды, из которой свет падает на границу раздела; α1 — угол падения света — угол между падающим на поверхность лучом и нормалью к поверхности; n2 — показатель преломления среды, в которую свет попадает, пройдя границу раздела; α2 — угол преломления света — угол между прошедшим через поверхность лучом и нормалью к поверхности. Если n1·sin α1 > n2, имеет место полное внутреннее отражение (преломлённый луч отсутствует, падающий луч полностью отражается от границы раздела сред). Закон Снелла хорошо определен для «геометрической оптики», т.е. в случае, когда длина волны достаточно мала по сравнению с размерами преломляющей поверхности, вообще же говоря, закон работает в рамках приближенного описания, каковым и является геометрическая оптика.
|
Рис. 1. Полное внутреннее отражение Рис. 2. Призмы полного внутреннего отражения
Полное внутреннее отражение, отражение оптического излучения (света) или электромагнитного излучения другого диапазона (например, радиоволн) при его падении на границу раздела двух прозрачных сред из среды с большим преломления показателем (ПП). П. в. о. осуществляется, когда угол падения i превосходит некоторый предельный (называется также критическим) угол iпр. При i > inp преломление во вторую среду прекращается. Впервые П. в. о. описано И. Кеплером. После открытия Снелля закона преломления стало ясно, что в рамках геометрической оптики П. в. о. — прямое следствие этого закона: оно обусловлено тем, что угол преломления j не может превышать 90° (рис. 1). Величина iпр задаётся условием siniпр = 1/n, где n — относительный ПП 1-й и 2-й среды. Значения n и, следовательно, iпр несколько отличаются для разных длин волн (частот) излучения (дисперсия света). При П. в. о. электромагнитная энергия полностью (отсюда — "полное") возвращается в оптически более плотную (с большим ПП) среду. Значение отражения коэффициента при П. в. о. превосходит его самые большие значения для зеркального отражения от полированных поверхностей и практически с высокой точностью равно 1. Кроме того, этот коэффициент при П. в. о., в отличие от зеркального отражения, не зависит от длины волны излучения (при условии, что для этой длины волны П. в. о. вообще имеет место) и даже при многократном П. в. о. спектральный состав ("цвет") сложного излучения не меняется. Поэтому П. в. о. широко используется во многих оптических приборах и экспериментах (см., например, Волоконная оптика, Отражательные призмы, Поляризационные призмы, Световод, см. рис. 2 и 3). Следует, однако, отметить, что энергия электромагнитных волн при П. в. о. частично проникает во 2-ю (с меньшим ПП) среду, но затем возвращается обратно. Глубина этого проникновения весьма невелика — порядка длины волны отражаемого света. |
Оптический путь. Принцип наименьшего оптического пути.
Распространение волн в омической среде. Скин-эффект.
Скин-эффект (от англ. skin — кожа, оболочка), поверхностный эффект, затухание электромагнитных волн по мере их проникновения в глубь проводящей среды, в результате которого, например, переменный ток по сечению проводника или переменный магнитный поток по сечению магнитопровода распределяются не равномерно, а преимущественно в поверхностном слое. С.-э. обусловлен тем, что при распространении электромагнитной волны в проводящей среде возникают вихревые токи, в результате чего часть электромагнитной энергии преобразуется в теплоту. Это и приводит к уменьшению напряжённостей электрического и магнитного полей и плотности тока, т. е. к затуханию волны.
Чем выше частота n электромагнитного поля и больше магнитная проницаемость m проводника, тем сильнее (в соответствии с Максвелла уравнениями) вихревое электрическое поле, создаваемое переменным магнитным полем, а чем больше проводимость а проводника, тем больше плотность тока и рассеиваемая в единице объёма мощность (в соответствии с законами Ома и Джоуля — Ленца). Т. о., чем больше n, m и s, тем сильнее затухание, т. е. резче проявляется С.-э.
В случае плоской синусоидальной волны, распространяющейся вдоль оси х в хорошо проводящей, однородной, линейной среде (токами смещения по сравнению с токами проводимости можно пренебречь), амплитуды напряжённостей электрического и магнитного полей затухают по экспоненциальному закону:
![]() ,
,
![]()
где
![]()
— коэффициент затухания, m0 —магнитная постоянная. На глубине х = d = 1/a амплитуда волны уменьшается в е раз.
Поглощение и рассеяние. Закон Бугера.
Как показывает опыт интенсивность света при прохождении через вещество убывает по экспоненциальному закону:
![]() .
.

Здесь I0 - интенсивность света на входе в поглощающий слой вещества толщиной x,
α - коэффициент поглощения, зависящий от длины волны (частоты) света.
Величина α, в соответствии с законом Бугера, не должна зависеть от интенсивности света. Это утверждение справедливо для очень широкого диапазона изменения интенсивности (примерно в 1020 раз), С. И. Вавилов экспериментально показал, что при больших интенсивностях для специально выбранных веществ коэффициент поглощения αуменьшается с ростом интенсивности. Происходит это потому, что для своих опытов Вавилов выбирал вещества у которых молекулы могут сравнительно долго (значительно больше, чем 10-8 с.) находится в возбужденном состоянии, в котором они не могут поглощать энергию от световой волны. В этом случае закон Бугера нарушается.

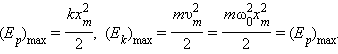

 1
1 2
2


 Рис.
3. Полное внутреннее отражение в струе
жидкости
Рис.
3. Полное внутреннее отражение в струе
жидкости