Определение1: Независимые события. Вероятность появления события A не меняет вероятности события B. Т.е. события называются независимыми, если реализация одного из них не оказывает никакого влияния на вероятность реализации другого. Определение 2: несовместные события. События называются несовместными, если они не могут произойти одновременно. Ответы: 1) Нет. События независимы по определению 1. 2) Вероятность Р(А+В) означает что произошло либо А либо В. Вероятность Р(А+В)=Р(А)+Р(В) = 1/2+1/2=1 3) Да. События независимы по определению 1. 4) Да. События независимы по определению 1. 5) Вероятность Р(А+В) это сумма вероятностей А и В. Р(А)=1/6, Р(В)=3/6=1/2. Вероятность Р(А+В)=1/6+3/6=4/6=2/3. 6) Вероятность Р(А*В) это означает что произошло и А и В. P(A*B) = P(A)*P(B) - вероятность одновременного наступления двух независимых событий равна произведению вероятностей этих событий. Вероятность Р(А*В)=0 т.к. 3 это не чётное число, а значит не будет выполнено условие. 7) По определению 2: События называются несовместными, если наступление одного исключает наступление другого. Пример. Элементарные исходы являются несовместными событиями при однократном опыте. Например, если мы бросили монету один раз, выпадет или решетка или герб, но, конечно, что-нибудь одно. События называются противоположными, если они сумме составляют всё пространство элементарных событий. Т.е. Р(А)+Р(противоположное А)=W, где W-пространство элементарных событий. Пример. Элементарные исходы являются противоположными при однократном опыте. Например, если мы бросили кубик, то вероятность выпадения тройки равна Р(А)=1/6, а событие противоположное А будет равняться 5/6. Т.е. всё что осталось. Вероятность Р(А+В)= Р(А+В)=Р(А)+Р(В)-Р(АВ), т.е. вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного появления 8) Если события несовместны то они независимы. Т.к. события не могут произойти одновременно, то P(A*B)=0 9) P(A*B) = P(A)*P(B) - вероятность одновременного наступления двух независимых событий равна произведению вероятностей этих событий. Если события зависимы то P(A*B)= Ответ: P(A*B) = P(A)*P(B) - вероятность одновременного наступления двух независимых событий равна произведению вероятностей этих событий.

Если события зависимы то P(A*B)=?

P(A*B) = P(A)*P(B) - вероятность одновременного наступления двух независимых событий равна произведению вероятностей этих событий.

Если события зависимы то P(A*B)=P(A)*Pa(B), т.е. равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое уже произошло 10) События зависимы. Вероятность Р(А+В)=1 потому, что противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице

11Дискретная случайная величина и закон ее распределения

Реальное содержание понятия «случайная величина» может быть выражено с помощью такого определения: случайной величиной, связанной с данным опытом, называетсявеличина, которая при каждом осуществлении этого опыта принимает то или иное числовое значение, причем заранее неизвестно, какое именно. Случайные величины будем обозначать буквами 

Определение. Говорят, что задана дискретная случайная величина   , если указано конечное или счетное множество чисел

и каждому из этих чисел   поставлено в соответствие некоторое положительное число   , причем

Числа   называются возможными значениями случайной величины   , а числа  - вероятностями этих значений (   ).

Таблица

называется законом распределения дискретной случайной величины   .

Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной системе координат строят точки   и соединяют последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины   .

Если возможными значениями дискретной случайной величины   являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:

то говорят, что случайная величина   имеет биномиальный закон распределения:

Пусть заданы натуральные числа m, n, s, причем   Если возможными значениямидискретной случайной величины   являются 0,1,2,…, m, а соответствующие имвероятности выражаются по формуле

то говорят, что случайная величина   имеет гипергеометрический закон распределения.

Другими часто встречающимися примерами законов распределения дискретной случайной величины являются:

геометрический

где   ;

Закон распределения Пуассона:

где

 - положительное постоянное.

Закон распределения Пуассона является предельным для биномиального при   ,  ,   . Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона:

где   . 

12. Непрерывные случайные величины

Определение 3.6   Случайную величину назовем непрерывной, если ее функция распределения непрерывна.

Легко видеть (см. Замечание 3.4), что случайная величина непрерывна тогда и только тогда, когда   при всех  .

Важный класс непрерывных случайных величин -- абсолютно непрерывные случайные величины. Это случайные величины, распределение которых имеет плотность.

Определение 3.7   Случайная величина   называется абсолютно непрерывной, если существует функция   такая, что

,

,

 имеет место равенство: 

Функция  , обладающая вышеперечисленными свойствами, называется плотностьюраспределения случайной величины  .

Следствие 3.1   Если   -- абсолютно непрерывная случайная величина, то

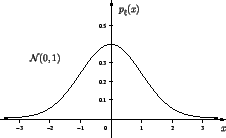
Наглядный смысл плотности можно проиллюстрировать следующим рисунком.

Замечание 3.5   Если плотность   непрерывна в точке  , то из Следствия 3.1вытекает следующее представление: 

Следствие 3.2   Если   -- точка непрерывности функции  , то

Примеры абсолютно непрерывных распределений

1) Равномерное распределение в отрезке 

2) Показательное распределение с параметром   

Показательное распределение называют также экспоненциальным.

3) Нормальное (или гауссовское) распределение  ,  ,  :

Стандартное нормальное распределение --  :

Упражнение 3.4   Найти функцию распределения   и построить ее график для примеров 1) и 2).

Упражнение 3.5   Проверить, что 

Упражнение 3.6   Пусть   --  . Показать, что   --  , если  .

Упражнение 3.7   Показать, что если   имеет нормальное распределение, а  ,  , то случайная величина   также распределена нормально.

13. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 

     Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X) = x₁ p₁+ x₂ p₂+...+ x_n p_n.       Реально на основе данных выборки мы не можем вычислить M(X). Однако эту характеристику можно оценить. В качестве оценки можно использовать среднее арифметическое, то есть M(X) ≈X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка. Математическое ожидание обладает следующими свойствами:       1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C.       2. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X).       3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z).       4. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(XYZ) = M(X)M(Y)M(Z). Все эти свойства имеют большое практическое значение.

14. Дисперсия и ее свойства. Среднее квадратическое отклонение.     Во многих практически важных случаях существенным является вопрос о том, насколько велики отклонения   случайной величины от ее математического ожидания.     Предварительно рассмотрим пример. Пусть две случайные величины   и   заданы следующими рядами распределения  

Значения	-0,2	-0,1	0,1	0,2
Вероятности p(x)	0,25	0,25	0,25	0,25

 

Значения	-50	-40	40	50
Вероятности p(x)	0,25	0,25	0,25	0,25

   Легко убедится в том, что математические ожидания этих величин одинаковы и равны нулю:  

   Однако разброс значений этих величин относительно их математического ожидания неодинаков. В первом случае значения, принимаемые случайной величиной  , близки к ее математическому ожиданию, а во втором случае далеки от него. Для оценки разброса (рассеяния) значений случайной величины около ее математического ожидания вводится новая числовая характеристика - дисперсия.     Дисперсией   случайной величины   называется математическое ожидание квадрата отклонения случайной величины от ее математичекого ожидания *:

(43)

   Пусть   - дискретная случайная величина, принимающая значения x₁, x₂, ..., x_n соответственно с вероятностями p₁, p₂, ..., p_n. Очевидно, случайная величина   принимает значения

с теми же вероятностями p₁, p₂, ..., p_n. Следовательно, согласно определению математического ожидания дискретной случайной величины, имеем

(44)

   Если же   - случайная величина с плотностью распределения  , то по определению

(45)

   Принимая во внимание определение дисперсии и свойства математического ожидания, имеем

   Так как   и   - постоянные, то используя свойства математического ожидания, получим

   Следовательно,

   Откуда окончательно находим

(46)

   Рассмотрим теперь свойства дисперсии.     1°. Дисперсия постоянной равна нулю. (Доказательство)     2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

(47)

(Доказательство)