Среднеквадратическое отклонение:

18. Нормальное распределение, также называемое гауссовским распределением или распределениемГаусса — распределение вероятностей, которое задается функцией плотности распределения: где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

19. Непреры́вное равноме́рное распределе́ние — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины. Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке  ,где ,если её плотность имеет вид:

Пишут: X∼U[a,b]. Иногда значения плотности в граничных точках х=а  и х=b меняют на другие, например 0 или .Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей.

17.Существо широко распространенного биномиального распределения может быть объяснено на следующей модели, к которой с той или иной степенью приближаются многие практические задачи и которая может быть сформулирована двояко.

1. Схема независимых испытаний. Пусть в результате отдельного испытания событие A может осуществляться с вероятностью n. Тогда число X появления события A в n независимых испытаниях будет случайной величиной, подчиненной биномиальному закону распределения.

2. Извлечение с возвращением. Пусть в множестве из N элементов содержится k элементов с признаком B. Вероятность выбора элемента с признаком B при случайном извлечении одного элемента равна  . Пусть производится n извлечений элементов из множества, причем после каждого извлечения и опознания элемента последний возвращается в множество. Пусть, наконец, эксперимент поставлен так, что при каждом извлечении вероятность p появления элемента с признаком B не меняется. Тогда число X извлечений элементов с признаком B подчинено биномиальному закону распределения.

Область x	0  x  n, x - целое
Параметры	n - целое положительное число (испытаний); p  (0, 1) - параметр схемы Бернулли (вероятность "успеха")
Плотность (функция вероятности)
Математическое ожидание	np
Дисперсия	np(1 - p)

График f(x) при n = 30, p = 0.2

Пример биномиального распределения

Представим себе файл в виде последовательности бит на жестком диске. Предположим, что вероятность встречи единицы постоянна для данного типа файлов. Тогда количество попавшихся единиц будет распределено по биномиальному закону.

Доказательство

Рассмотрим одно из возможных состояний, возникающее в результате встречи m единиц и n - m нулей. Вероятность этого конкретного состояния будет равна p^m(1 - p)^n - m. Однако m единиц и n - m нулей могут встретиться различными способами. Количество этих способо равно  . Из этого следует, что вероятность возникновения любого из состояний, при которых встречаются m единиц и n - m нулей равна  . Конечная формула совпадает с формулой плотности биномиального распределения.

20.Системы случайных величин

Здесь мы рассмотрим системы случайных величин или по другому их называют cлучайные векторы.Мы рассматривали случайные одномерные величины, которые можно отобразить точкой на числовой оси. Этой величине ставилась в соответствие то, что мы называли вероятностью появления возможного значения случайной величины.

Но кроме одномерных существуют и другие величины, которые для своего полного описания требуют большего набора переменных. Например, чтобы отобразить положение точки на плоскости, или положение точки в пространстве. Соответственно потребуются двух- и трехмерные величины . Их называют векторами или системами случайных величин. Существуют и N-мерные величины, и их по аналогии называют N-мерными векторами или N-мерными системами.

Принято для двумерной системы использовать обозначение (X,Y), трехмерной - (X,Y,Z), N- мерной - (X1 , X2 , ... Xn).

Каждую из величин X,Y,Z называют составляющими системы. Если составляющие дискретны , то система называется дискретной ; если составляющие непрерывны , то система называется непрерывной.Отметим, что по одному из определений система – это целое, состоящее из частей, связанных единой функцией.

частное распределение,- распределение случайной величины или множества случайных величин, рассматриваемых в качестве компоненты или множества компонент нек-рого случайного вектора (см. Многомерное распределение) с заданным распределением. Иначе, М. р. является проекцией распределения случайного вектора Х=( Х ₁, . . ., Х _п).на любую ось х ₁ или подпространство, определяемое переменными   и полностью определяется по распределению этого вектора. Напр., если F( х ₁, х ₂) -функция распределения Х=(X₁, X₂) в   то функция распределения X₁ равна   если двумерное распределение абсолютно непрерывно и р( х ₁, х₂).- его плотность, то плотность М. р. Х ₁ равна 

Аналогично вычисляется М. р. для любой компоненты или множества компонент вектора Х=( Х ₁, ..., Х _п).при любом п. Если распределение Xнормально, то все М. р. также нормальны. В том случае, когда величины Х ₁, ..., Х _п взаимно независимы, по М. р. компонент Х ₁, ..., Х _п вектора Xоднозначно определяется его распределение:

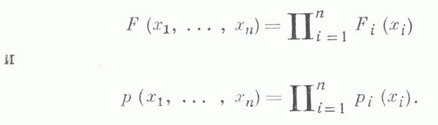
Аналогично определяется М. р. по отношению к распределению вероятностей, заданному на произведении пространств, более общих, чем числовая прямая.

Коэффициент корреляции.     Как мы знаем, если   и   - независимые случайные величины, то по свойству математического ожидания

(72)

   Если же   и   не являются независимыми случайными величинами, то, вообще говоря,   

   Условились за меру связи (зависимости) двух случайных величин   и   принять безразмерную величину  , определяемую соотношением.

(73)

   и называемую коэффициентом корреляции.     Рассмотрим некоторые свойства коэффициента корреляции.     Если   и   - независимые случайные величины, то коэффициент корреляции равен нулю.     Это свойство непосредственно вытекает из соотношений (72) и (73). Заметим, что обратное утверждение, вообще говоря, неверно, т. е. если  , то отсюда еще не следует, что   и   независимы.     Заметим без доказательства, что  . При этом если  , то между случайными величинами   и   имеет место функциональная, а именно линейная зависимость.