6. Пример построения математической модели каталитического процесса в пористой грануле.

Каталитич процесс в пористой грануле

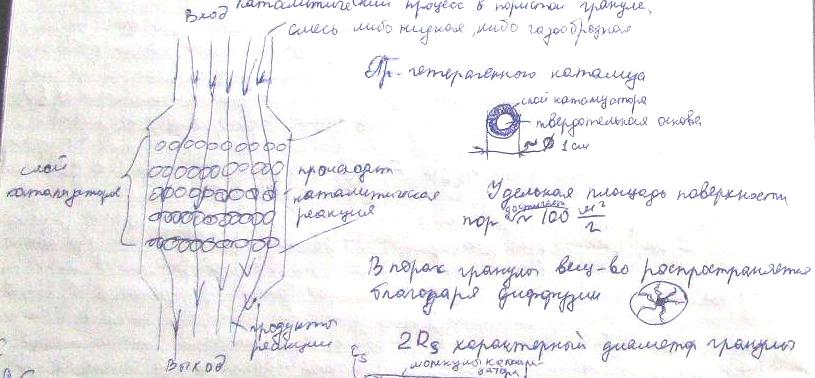
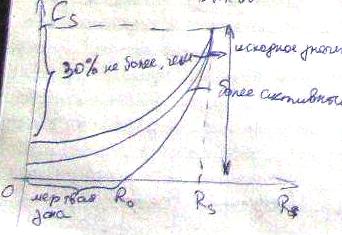
C-концентрация исх вещ-ва; С_s-концентрация на входе

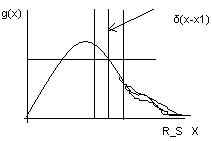
Скоростью хим реакции

g (x)-плотность каталитич центров на единицу объема гранулы

то эксперименты результата практически не отличаются от теоретических полученных в предположении распределении каталитических центров в виде дельта функций. В некоторых случаях можно существенно повысить эфор-ть пористых гранул католизатора, если реагентов менять по определенному закону во времени концентрацию температуру на входе.

7. Моделирование каталитической реакции первого порядка в пористой грануле.

. А1--r1--> продукты; r1- скорость каталитической реакции, рассчитанная на единицу объема пористой гранулы. Т=const.

1. Процесс изотермический (Т(x,t)=const)

2. Поры распологаются радиально (вдоль радиуса) начинаются на внешней поверхности и заканчиваются в центре границы.

3. Перенос вещества А₁ и продуктов в порах осуществляется за счет дуффузии и диффузия подчиняется закону Фика 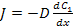, J- плотность потока диффузии, D – коэффициент диффузии, – концентрация вещества А₁.

4. Будем считать, что D=const, D зависит от концентрации вещества и температуры.

5. Будем считать, что справедлива квазигомогенная модель (т.к. к центров очень много, то можно считать, что они находятся в жидкой форме. В квазигомогенной модели реагенты находятся в той же среде, что и реагенты).

- эффективный коэффициент диффузии. подвергается так, что в результаты эксперимента совпали с требуемой степенью точности с результатами вычислений по квазигомогенной модели.

2Rs

S

Д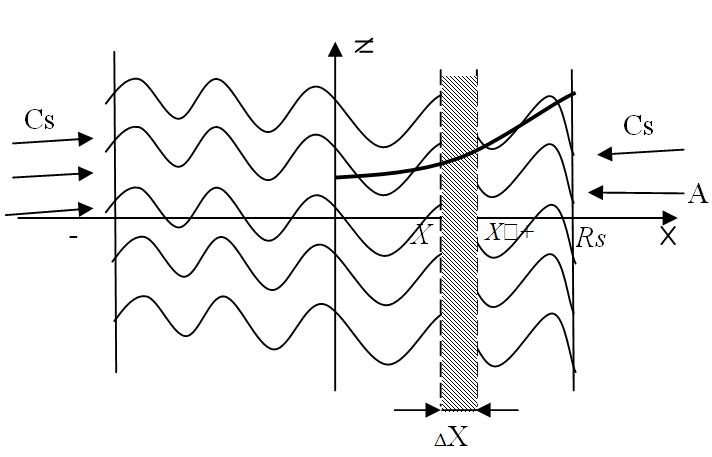 ля простоты рассматриваем одномерную модель.

Д

Rs

-Rs

X₁+ ΔX

ΔX

X₁

ля упрощения. На границе (в близи границы) процесс будет протекать по другому. Если границыне учитыватьбудет описываться таким же уравнением. Будем считать, что потоки справа и слева одинаковы. Будем считать, что картина полностью симметрична относительно оси Z.

В данном случае, чтобы упростить модель будем считать, что пограничный слой отсутствует. Cs₁ - концентрация вещества A₁ во внешней среде.

Грничные условия: ;

S – площадь передней грани паралеллепипеда.

Составляем уравение баланса вещества для выделенного слоя

Вещество на поверхности пор не абсорбируется. Процес стационарный, т.е. концентрация вещества не зависит от времени

; ; ;

. Пусть , тогда .

Квазигомогенная модель, описывающая, совместимый процесс диффузии и каталитической реакции в пористой грануле катализатора. – довольно часто имеет такой вид(n – порядок реакции).

(граничные условия) ;

;

;

; ; ; ; ; ;

Sh2 = 2Sh ; ; ; ;

; ; ;

X=0;

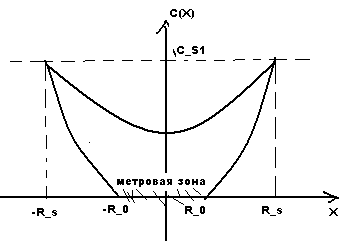
в центре гранулы концентрация;

k-характеризует скорость протеканиря реакции;

r=kC чем к-выше тем выше скорость реакции.

-->Y(0)=0.