4.2Оптимальная аппроксимация функции с использованием ортогональных полиномов Чебышева.

При использовании классической формы МНК возникает необходимость повысить степень полинома, если вычисление с его помощью значения у сильно отличается от наблюдённых. В этом случае следует производить пересчет всех коэффициентов аi , полученных ранее.

Здесь следует иметь в виду ещё и то обстоятельство, что для случая обработки неточных наблюдений значений уi уменьшение значения Ф в (2) происходит лишь до

mopt , после которого повышать степень полинома нецелесообразно, так как Ф снова начнет возрастать. Эту ситуацию можно пояснить с помощью графика Ф=Ф(m) (рис.1)

Способ Чебышева позволяет найти mopt , при этом приближающий многочлен ищется здесь в виде суммы многочленов повышающихся степеней, причем добавление новых слагаемых не изменят коэффициентов при предыдущих.

При этом, как и прежде, предполагается, что степень многочлена m значительно меньше числа наблюдений n.

Суть метода Чебышева состоит в том, что приближающий многочлен находиться (строиться) в виде суммы многочленов, выбранных специальным образом:

Суть метода Чебышева состоит в том, что приближающий многочлен находится(строится) в виде суммы многочленов, выбранных специальным образом.

Смоделируем метод Чебышева для интерполяции функции f(x) ,

на интервале [0,2]

Исходные данные:

- число узлов интерполирования

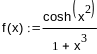
Вычисляем полином первой степени:

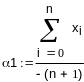
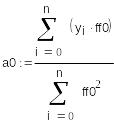
Находим коэффициент а1:

- полином первой степени

- сумма квадратов отклонений

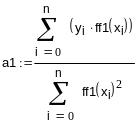
По этим же формулам рассчитываем полиномы 2, 3, 4 и 5 степени.

- полином второй степени

- сумма квадратов отклонений

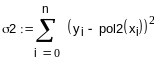
- полином третьей степени

- сумма квадратов отклонений

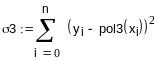
- полином 4-ой степени

- сумма квадратов отклонений

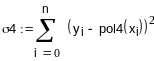
- полином 5-ой степени

- сумма квадратов отклонений

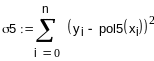
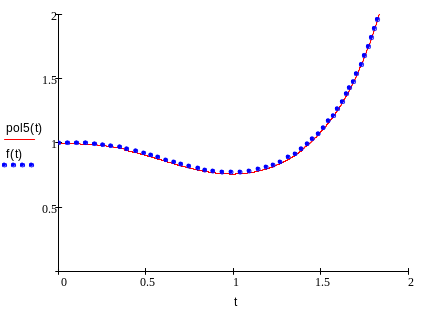
По графику видно, что найденный нами полином даёт значения, близкие к действительным значениям данной функции. Отклонение от истинных значений функции минимальное.

5.Численные методы интегрирования

5.1 Метод трапеций

Общий подход к решению этой задачи заключается в том, что мы находим определенный интеграл от функции, заменяя интеграл площадью фигуры, заключенной под функцией на заданном интервале. Площадь этой фигуры считаем примерно равной площади трапеции.

Наш заданный интервал - [1,5] разбиваем на множество отрезков, меньших интервала и считаем интеграл как сумму площадок этих полосок.

Метод трапеций – приближенный метод, потому что когда мы считаем площадь трапеции, то заменяем кривую на прямую. Для каждой маленькой трапеции эта погрешность своя. Сумма погрешностей должна давать то самое отклонение полученного значения от истинного.

Тогда величину определённого интеграла можно оценить:

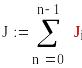
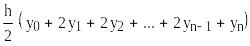
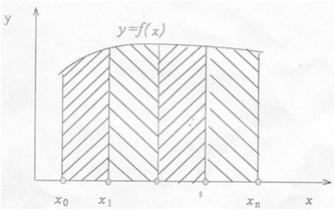
Вычисление определенного интеграла

Эта формула описывает хорошо извсетсное правило трапеции для численного интегрирования. Это один из простейших методов численного интегрирования.

Ошибка ограничения для метода трапеций.

Предположим, что y = f(x)

C²_[a,b] - непрерывная вместе со своими

первой и второй производными на [a,b] функция. Остаточный член на i-м участке равен:

Дифференцируя формулу (5.4) по h последовательно два раза, получим

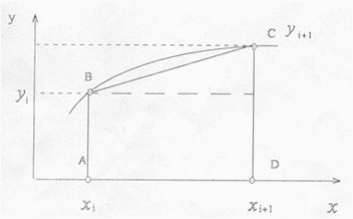
Рис.5.2. Вычисление площади частичного отрезка.

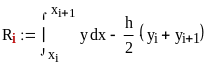
Для вычисления ошибки округления составим граф вычислительного процесса правила трапеций (см.рис.5.3.). Предполагается, что все члены суммы, которые необходимо умножить на 2, сначала складываются, а их сумма умножается на 2.

Пусть d _i (i = 0,1,...,n) относительные ошибки каждой величины y_i. Пусть a относительная ошибка операции сложения, m - относительная ошибка операции умножения. Тогда относительная ошибка округления для формулы вычисления интеграла по правилу трапеции (5.3) в соответствии с графом вычислительного процесса можно вычислить:

где К - символ, заменяющий многоточие.

Абсолютная ошибка равна:

Положим d = d0 = d1 = K = dn,

Положим

где f - коэффициент пропорциональности;

среднее из всех y_i.

Тогда

Учитывая, что

, имеем

Тогда

При малом h (большом n) главная часть ошибки округления в формуле (5.12) заключена в члене n², поэтому можно дать следующую верхнюю оценку e_I :

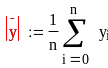
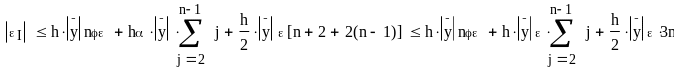
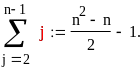
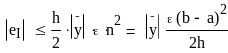
Решение задачи заключается в разбиении отрезка[a,b]

на множество отрезков меньших размеров и вычислении интеграла как суммы, приближенно вычисленных площадей полосок, получившихся при таком разбиении.

Исходные данные:

Число интервалов разбиения отрезка:

Функция для вычисления интеграла методом трапеций:

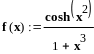
длина каждого отрезка

площадь, лежащую между

точками будем приближенно

вычислять как площадь трапеции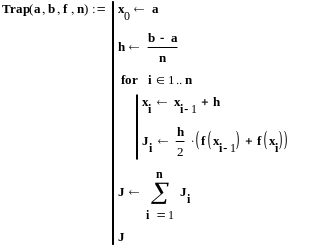

Вычисление определенного интеграла с

помощью стандартной функции Mathcad

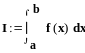
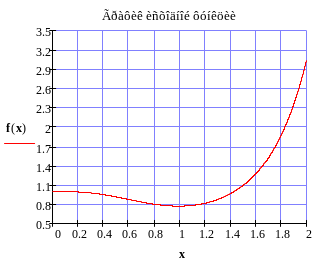
Ошибка при расчете методом трапеций:

Конечный результат вместе с ошибкой:

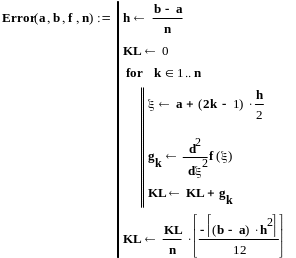
Тогда остаточный член

Ошибка округления

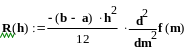
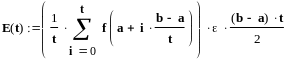
По графику видно, что оптимальный шаг

Как можно увидеть, последнее полученное значение не совпадает с истинным значением. Это можно объяснить тем, что отклонение на каждом участке грубо подсчитано, а также сам метод трапеций не точный. Если уменьшить или увеличить шаг h, то суммарная ошибка только увеличится. Существует оптимальное h при котором ошибка минимальна. В нашем случае оптимальное значение h равно 8.

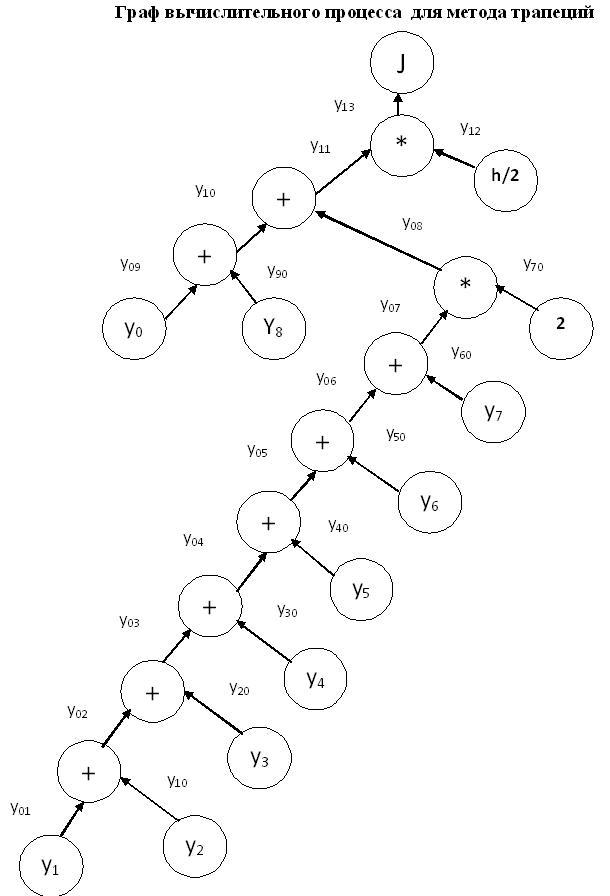
Определение погрешности с использованием графа вычислительного процесса
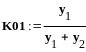
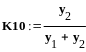
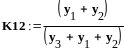
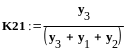
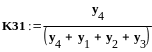
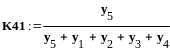
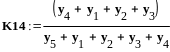
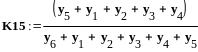
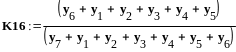
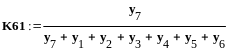
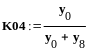
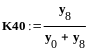
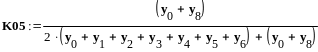