1).Числовые ряды

Опр. числовой ряд. Опр. Ряд наз-ся сход-ся, если ; S – сумма ряда; Необходимый признак сходимости ряда: Если ряд сход-ся, то

Св-ва сх-ся рядов: 1). Если сх-ся к сумме S, то , где , сх-ся к сумме 2). Если и сх-ся, то сх-ся ряд, то сх-ся. 3). Если сх-ся, то сх-ся ряд, полученный отбрасыванием конечного числа слагаемых.4).

2).Признаки сх-ти неотриц.Рядов

Для того, чтобы зпакоположит. ряд сх-ся, необходимо и достаточно, чтобы последов. его частичных сумм была ограничена. Признаки сх-ти: 1). Признак сравнения: Даны 2 знакополож. ряда и . Пусть , тогда а). Если сх-ся ряд , то сх-ся б). Если ряд рас-ся, то рас-ся . 2). Предельный признак сравнения: Пусть для знакополож. рядов , выполняется , тогда ряды ведут себя одинаково, т.е. оба сх-ся или рас-ся. 3). Признак Даламбера: Пусть для знакополож. , тогда а). Если d<1 ряд рас-ся. б). Если d>1 рас-ся.

3).Знакоперем.Ряды.

Опр.Ряд - наз-ся абсолютно сх-ся, если сх-ся ряд Опр. Если ряд , а ряд рас-ся, то ряд наз-ся условно сх-ся. Признак Лейбница: Если , и последовательность , начиная с некоторого номера , стремится к 0, то ряд сх-ся.

4).Функ-ные ряды

Ряд наз-ся функцион. рядом. Давая репеменной x определ. числовые знач-я, получаем числовые ряды. Если в ряд сх-ся, то - точка сх-ти. Если рас-ся, то – точка рас-ти. Опр. наз-ся равномер. сх-ся в области D, если Признак Вейерштрасса Выполняется – знакоположит. сх-ся ряд, тогда равномерн. сх-ся Д-во: т.к. сх-ся, то выполняются ; Для фун-го ряда остаток: ; выполняется опред. равномер. непрерыв. ряда.

5).Степ.Ряды

Опр. Ряд вида – степ. ряд. Теорема Абеля а). Если степ. ряд – сх-ся в , то он сх-ся абсолютно в интервале т.е. Д-во: т.к. - сх-ся, то выполняется необход. признак Запишем степ. ряд в виде: ; ; – геометрич. ряд со знаменат. сх-ся при по признаку сравн-я степ. рядов сх-ся абсолютно. б). Если степ. ряд рас-ся в , то он рас-ся Д-во: Если ряд сх-ся только в x=0 R=0 во всех точках x R=

6).Радиус сх-ти, св-ва степ.Рядов

Каждый степенной ряд сх-ся абсолютно внутри некоторого круга |z-a|≤R, где радиус круга R≥0 определяется по формуле Коши-Адамара или по ф-ле ,если этот предел хотя бы в несобственном смысле. Св-ва степ. рядов 1). Пусть имеет интервал сх-ти (-R, R), тогда он равномер. сх-ся на любом промежутке [-r, r], где 0<r<R 2). Сумма явл. непрерывной фун-ей в каждой точке его интервала сх-ти. 3). можно диф-ать в любой точке интервала сх-ти 4). можно интегрировать. Разл. ф-ции в степ. ряд: Пусть Говорят, что ф-ция раскладывается в степенной ряд на интервале [a-R, a+R], где 0<R≤min( ), если , такое, что справедливо равенство .

7).Период.ф-ции

Опр. Фун-я наз-ся периодич. с периодом T=0, если kT – период k=±1,±2… Опр. Система ненулевых ф-ций наз-ся ортогональной на промежутке [a,b], если при n≠m. Опр. Система - наз-ся тригонометрич. системой на [-π,π] ортогональность: a). ; b). ; c). ; d). ; e). Д-во: ;

8).Тригон.ф-ции

Опр. Фун-ций ряд - наз-ся тригонометрич. Пусть Числа , наз-ся коэффициентами Фурье ф-ции f по основной тригонометрич. системе.

10).Ф-ции многих перемен.

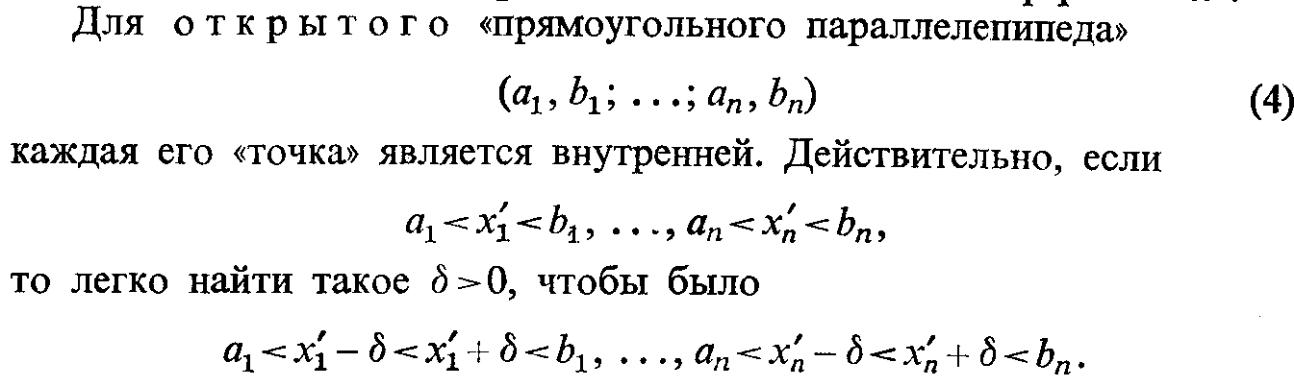
11).Предел и непрерыв.ф-ции

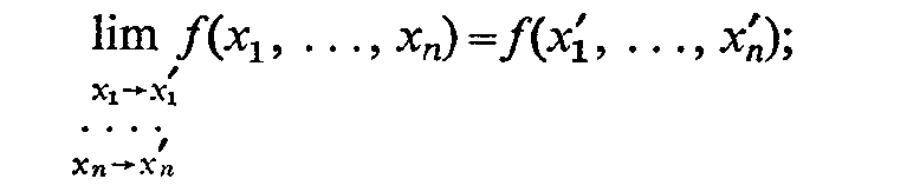
12).Частные производ.

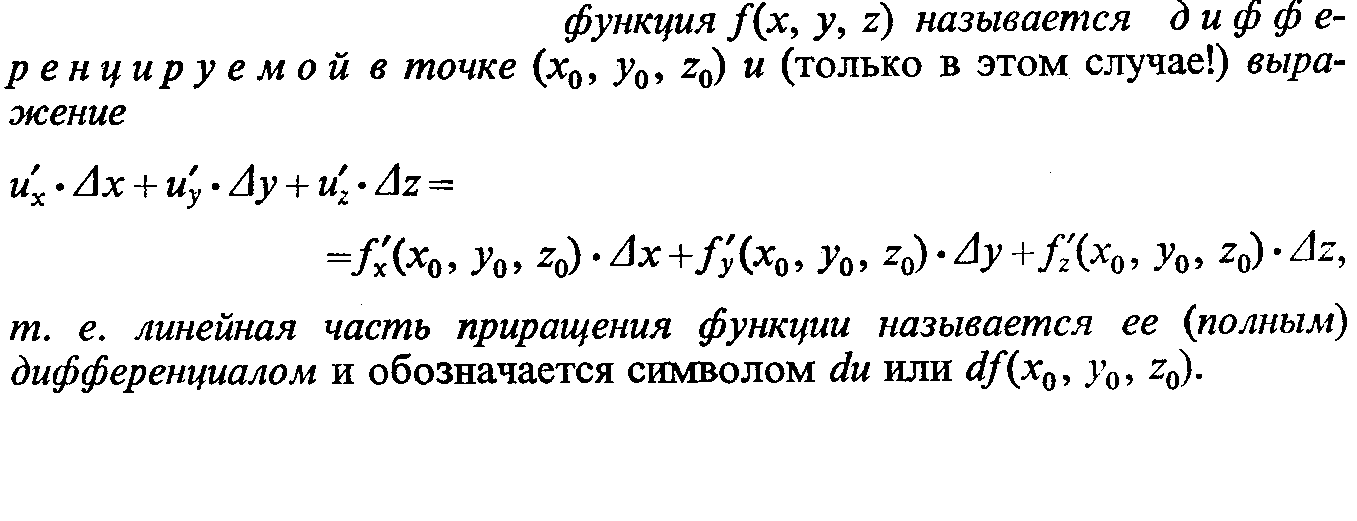
13).Диф-ние сложной ф-ции

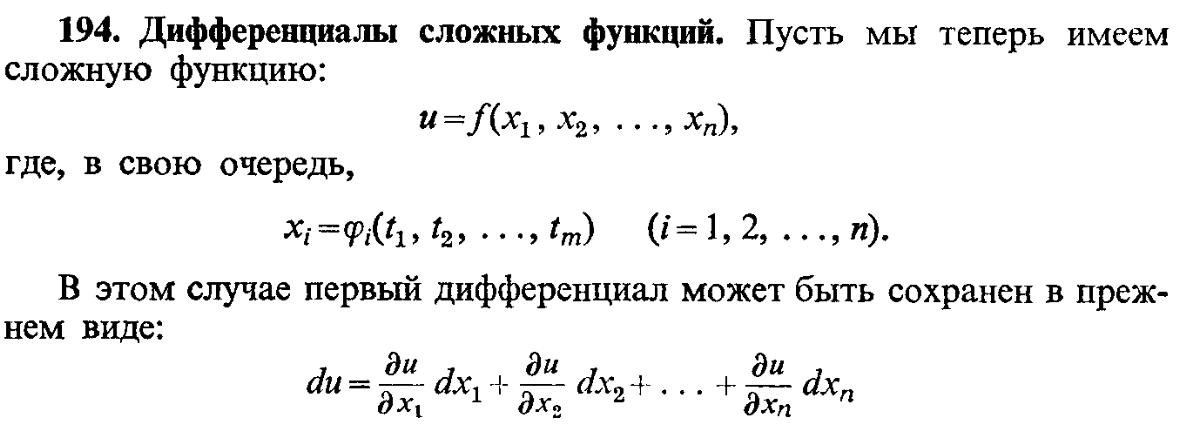
14).Произв.и диф-ал слож.ф-ции

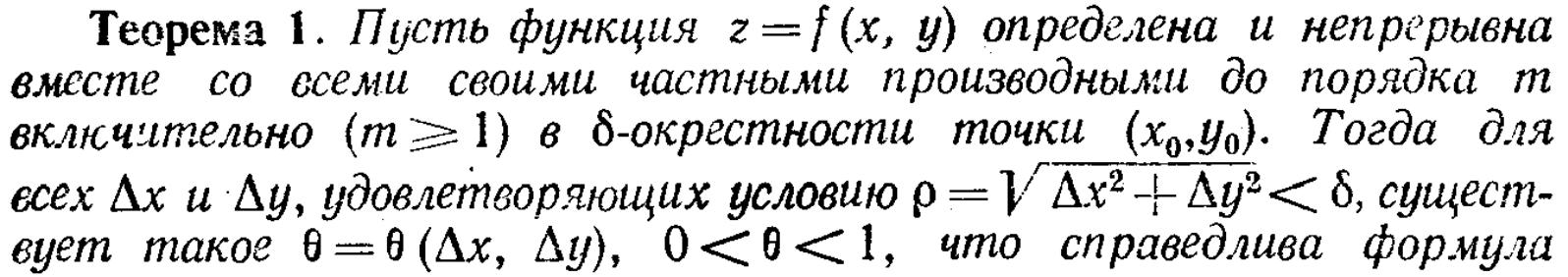
где

15).Произв.неявно заданной ф-ции

16).Произв по направлению.

;

; зададим прямую L проходящую через M

Произв. от в точке M то по напрв. над , где

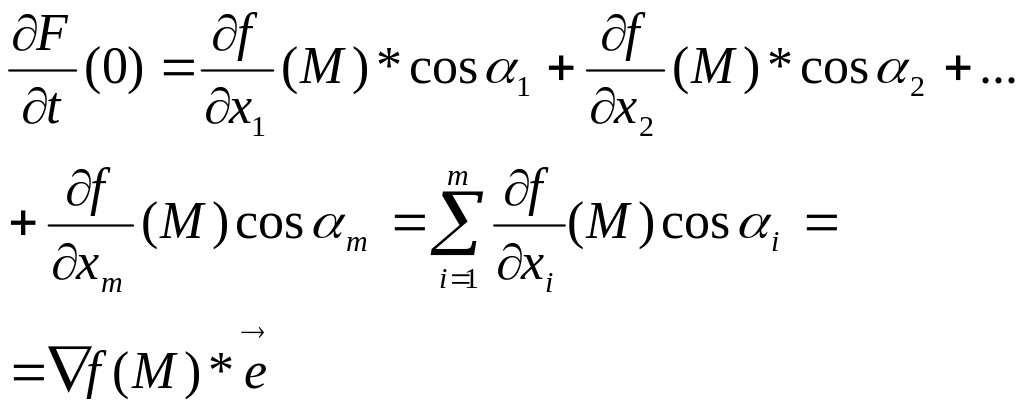
F(t)= .Получим для сложной функции - градиент f в точке M. 17).Градиент

Производная по направлению от f равна градиенту в этой точке единичного вектора дополнительного направления.

Свойства градиента.

1). Градиент не зависит от выбора системы координат.

2). Если градиент фу-ии f то направление градиента является тем же единственным направлением , по которому произв-ая достигает max значение в данной точке.

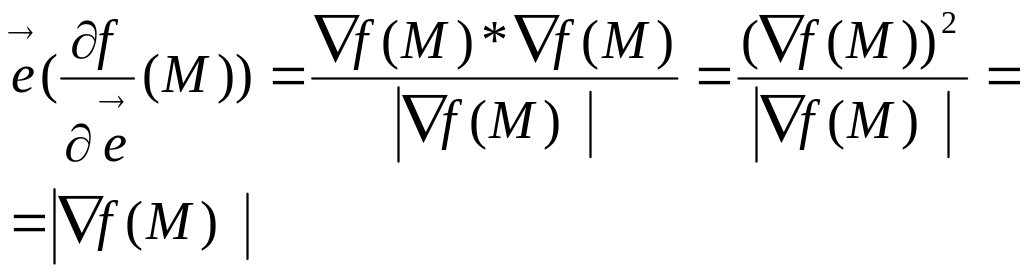
L среднее.

18).Экстремумы достаточный признак экстремума: