35).Геометрич. И физич. Прилож.

;

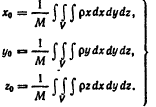
36).Обыкнов.Диф-е ур-я

Обыкновенные дифференциальные ур-я

Дифференциальным ур-ем называется ур-е связывающее независимую переменную х, искомую фун-ю у=b(х) и производные у^’,y^’’…,y⁽ⁿ⁾,Если искомая функция зависит от одной переменной ур-е называется обыкновенным.

Если зависит от нескольких переменных и производная частная, то ур-е называется дифференциальным ур-ем с частной производной.

Наивысший порядок производной неизвестной функции называется порядком дифференциального ур-я.

Пример: у^’-2ху²+5=0 – дифференциальное ур-е 1-го порядка. Решением диф-ного ур-я называется всякая функция у=b(х) подстановка которой в ур-е представляет его в тождество.

Опр. Решение ур-я заданное неявно Ф(х,у,с)=0 называется общим интегралом.

Опр. График любого решения называется интегральной прямой.

Диф-ое ур-е 1-го порядка.

Опр. Общий вид диф-го ур-я 1-го порядка имеет вид F(х,у,у^’)=0,

у^’=b(х,у)- уравнение, разрешенное относительно производного.

Теорема (Существования единственности решения диф. ур-я). Если в ур-ии у^’=b(х,у) функция b(х,у) и её частная производная по у непрерывны внекоторой области D плоскости ХОУ, содержащей некоторую точку (х₀,у₀), то существует единственное решение данного ур-я удовлетворяюшее условию при х=х₀ . функция у=у₀.

Опр. Задача Коши для ур-я у^’=b(х,у) состоит в нахождении решения этого ур-я удовлетворяющее условию у]_x=x0=y₀ , которое называется начальным условием.

37).Диф-е ур-я с раздел. перемен

Ур-ние вида , где - заданные непрерывные ф-ции, , наз-ся дифференциальным ур-нием с разделяющимися переменными.

38).Однор. Ур-я 1-го порядка

Ур-ние вида , где M, N –непрерывные в некоторой области и однородные ф-ции одной и той же степени, наз-ся однородным.

39).Линей. Диф-е ур-я 1-го порядка

Линейные ур-я первого порядка .

Опр. Лиин. ур-ем первого порядка называется уравнение линейное относительно неизвестной функции и производной (1) , где Р(х), Q(х)- непрерывные функции. Решение будем искать в виде произведения двух ф-ий у=U(x)*V(x).

подставим в ур-е (1)

- это ур-е с разделяющимися переменными находим V(x) , находим U(x)

Уравнение Бернулли

Опр. Ур-е вида α≠1

называется уравнением Бернулли.

Замечание: 1) α=1

ур-е с разделяющимися переменными.

2) α=0 + P(x)y=Q(x) – это линейное уравнение 1-ого порядка.Решение ищем в виде произведения двух функций y=U(x)*V(x).Подставим в урав-е Бернули:

находим фун-ю V(x)

находим фун-ю U(x)

40).Метод вариации постоян

Наиболее употребительным способом решения линейного ур-я первого порядка явл-ся метод вариации постоянной. Сущность метода состоит в следующем: сначала ищется решение однородного ур-я . Затем в общем решении этого ур-я произвольную постоянную C считают некоторой диф-емой ф-цией от x:C=C(x) . Эту ф-цию находят из диф-ного ур-я с разделяющимися переменными, которое получается в результате подстановки общего решения ур-я в линейное ур-е первого пордяка.

41). Диф-е ур-я с полн. диф-лом.

Опр. Урав-е вида P(x,y)dx+Q(x,y)dy=0, где

- назыв-ся урав-ем с полным дифференциалом

Выраж-е в левой части урав-я является полным дифференциалом некоторой фун-ции U(x,y)., т.е. du(x,y)=0

После интегрирования этого ур-я получим

U(x,y)=const

Т.к. левая часть ур-я полный дифференциал, то выполняется из этих равенств находим фун-ю U(x,y)

42).Диф-е ур-я высш. порядков

Дифф. урав-я высших порядков:

F(x,y,y',y'',…,y⁽ⁿ⁾)=0 – диф. урав-е n-го порядка или y⁽ⁿ⁾=f(x,y,y’,…,y^(n-1)) – это урав-е разреш-ое относ-но старшей произв-ой

Теорема (существование и единственность решения)

Если в ур-нии y⁽ⁿ⁾=f(x,y,y’,…,y^(n-1)) фун-я f(x,y,y’,…,y^(n-1)) непрерывны в некоторой области, содержащей значения x=x₀, y=y₀, y’=y₀’,…,y^(n-1)=y₀^(n-1), то сущ-ет единств-ое решение y=y(x), удовлетвор-ее урав-ию и условиям ,

….

(Эти условия наз-ся начальными условиями)

Опр.Общим решением дифф. урав-ия n-ого порядка наз-ся фун-я y=φ(x,c₁,c₂,…,c_n) зависящая от n произвольных постоянных c₁…c_n, удовлетворяющих данному условию

Опр. Всякая фун-я полученная из общего решения при конкретных значениях c₁…c_n (т.е. при конкретных начальных условиях) назыв-ся частным решением.

Для определения частного решения можно использовать краевые условия, т.е.

43).Диф-е ур-я 2-го порядка

Урав-е вида не содержит в явном виде фун-ю y. В этом случае делают замену.

, тогда - это ур-е первого порядка

Из этого ур-ия находим фун-ю P

А из соотношения находим фун-ю y.

2) Ур-е вида не содержит в явном виде независимую переменную x

, но P-фун-я переменной y (а не x)

, - это ур-е 1-ого порядка. y находим P(y), из находим y(x)

44).Лин-е диф-е ур-я n-го порядка

Опр. Линейным диф. урав-ем n-ого порядка назыв-ся урав-ем вида

a₀y⁽ⁿ⁾+a₁y^(n-1)+a₂y^(n-2)+…+a_ny=f(x)

где a₀,a_1,…,a_n – ф-ции от переменной x

Если f(x)=0 ур-е наз-ся линейным однородным ур-ем.

Если f(x)≠0 неоднородное ур-е или ур-е с правой частью

Далее будем рассматривать ур-е второго порядка.

Теорема Если y₁ и y₂ – решения линейного однородного ур-я 2-ого порядка

1) y''+a₁y’+a₂y=0, то 1) y₁+y₂ – решение ур-я 1) 2) const*y₁ –решение 1)

Док-во:

Т.к. y₁,y₂ – решения, то y₁''+a₁y₁’+a₂y₁=0,

y₂’’+ay₂’+a₂y₂=0 Подставим в 1) y=y₁+y₂

(y₁+y₂)’’+a₁(y₁+y₂)’+a₂(y₁+y₂)=0

y₁’’+ y₂’’+a₁y₁’+ a₁y₂’+ a₂y₁+ a₂y₂=0 0=0, ч.т.д.

Замечание Из теоремы следует что множество решений однородного линейного ур-я второго порядка является линейным пространством