19).Наибол.И наим.Знач-е ф-ции

20).Ф-лы для выч-я произ 2 пор-ка при зам

№21. Определение двойного интеграла. Его свойства (перечислить).

Опр. Предел интегральных сумм при мелкости разбиения, стремящейся к нулю, называется 2-ым интегралом от функции f(x,y) по области D(не зависит от способа разбиения и выбора точек P(i)). Осн. св-ва 2-го интеграла:

1) Площадь: S- площадь области D.

2) Линейность

3) Аддитивность. D=D1UD2

4) Монотонность. Если f(x,y)<=g(x,y) в области D, то:

5) Оценка модуля.

6) Для множества функций f(x,y) имеет место неравенство:

где М=max|f(x,y)|, S-площадь D. Док-во: |f(x,y)|<=M, по св-ву 5;

далее по св-ву 2=>

№22 Сведение двойного интеграла к повторному.

Пусть задана область D={(x,y)=> a<x<b},

- Непрерывные функции. Опр. называется повторным интегралом.

Теорема. Если f(x,y) непрерывна в области D ={(x,y):a<x<b}, тогда: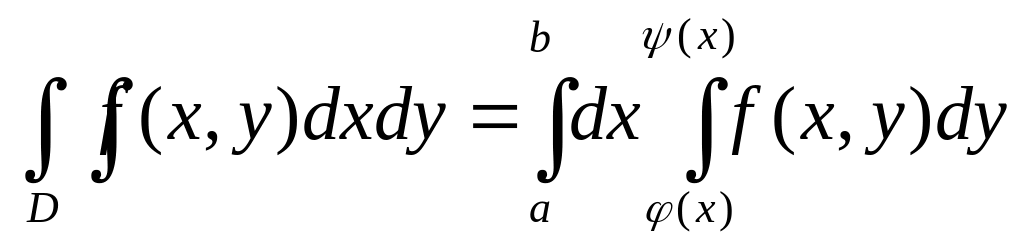

Вывод: для вычисления двойного интеграла следует вначале проинтегрировать фун-ию по переменной y, после чего проинтегрировать получившуюся функцию по переменной x.

23)Опр. И св-ва тройн. Интегр

св-ва тройного интеграла: №24 Сведение тройного интеграла к повторному

Правильной относительно оси Z называется трехмерная область вида: G={(x,y,z) : (x,y) принадлежит D} и непрерывные функции. Зафиксируем точку (x0,y0) => f(x0,y0,z), где f функция одной переменной, а значит она непрерывна.

Опр. - наз-ся повторным .Тогда справедлива формула:

Сначала вычисляется интеграл по Z. При вычислении тройного интеграла по области, правильной относительно оси Z следует, вначале считая (x,y)=const проинтегрировать по переменной Z, а затем от получившейся функции взять двойной интеграл по проекции области на плоскости Oxy.

№25. Замена переменной в двойном интеграле. Полярные координаты.

Пусть u,v новые переменные, взятые за место x,y. При замене переменной область D переходит в область D1.

I= Формула замены переменной:

Полярные координаты:

p>0 – расстояние от начала координат до точки.

I= =p

26).Цилиндр. И сферич. Корд

Цилиндрические координаты:

=I=

Сферические координаты _,

+ = ² cos

27).Опр. И св-ва крив.Инт.1-го рода

z=f(x,y) определена в точках дуги АВ. Разбивает дугу АВ точками А=А₀, А₁, …А_n=В произвольным образом. Обозначим S_k – длина дуги А_k-1 A_k . M( _k.. _k) A_k-1A_k Составим сумму _k Опр. Криволинейным интегралом I рода по кривой АВ от фун-ии f(x,y) назыв-ся предел Lim (ds - дифференциал дуги) Формулы для нахождения криволинейн. интеграла:

1)Кривая АВ задана урав-ем y= , где x [a, b] ²dx 2) AB задана параметрически: x=x(t), y=y(t)

dt 3) АВ – пространственная кривая x=x(t), y=y(t), z=z(t) dt

Свойства кривол. интеграла I рода: 1)Кривол. интеграл I рода независит от движения по кривой (от т.А к В или наоборот.

2) Линейность f(x,y)ds+ 3)Аддитивность АВ=АС СВ

. Физический смысл интеграла I рода: если считать фун-ю f(x,y) плотностью массы распределенной вдоль АВ, то -масса кривой АВ.

28).Опр. и св-ва крив.инт.2-го рода Пусть на кривой АВ заданны фун-ции P(x,y) и Q(x,y) X_k – проекция дуги A_k--1 A_k на ось ОХ У_К – проекция - - - - на ось ОУ составим суммы X_K Y_k

1)Криволинейный интеграл II рода по координате Х называется Lim

X_K= 2) - - - - по координате у Lim Y_K= 3)Полный криволинейный интеграл II рода

Замечание =

Формулы для вычисления

1) y= - кривая АВ = = ^/(х)dx 2) x=

= ^/(t)dt

^/(t)dt