
- •Обчислювальний експеримент. Теорія попиту.
- •Абсолютна і відносна похибки
- •Методи розв’язання системи лінійних рівнянь (слр). Прямі методи слр.
- •Метод Гауса чисельного розв’язку слр.
- •Вивід розрахункових формул
- •Модифікація методу Гауса
- •Умови застосування методу Гауса і його зв'язок з розкладом матриці на множники.
- •Обчислення визначника
- •Обчислення обернених матриць
- •Обумовленість с-ми лінійних рівнянь Стійкість слар
- •Обумовленість слар, число обумовленості
- •Метод прогонки для розв’язання слар
- •Ітераційні методи розв’язання слар
- •Ітераційний метод Якобі
- •Ітераційний метод Зейделя
- •Канонічна форма однокрокових ітераційних методів
- •Приклад розв’язання методом Зейделя та Якобі
- •Метод простої ітерації
- •Дослідження збіжності ітераційних методів
- •Необхідна і достатня умова збіжності у стаціонарних методах
- •Оцінки швидкості збіжності стаціонарних ітераційних методів
- •Многочлени Чебишева 1-го роду і многочлени Чебишева на відрізку [0,1]
- •Многочлен Чебишева на проміжку [a,b]
- •Ітераційні методи Чебишовським набором параметрів
- •Неявний Чебишевський ітераційний метод
- •Інтерполяція функцій
- •Інтерполяційний многочлен Лагранжа
- •Розділені різниці. Інтерполяційний многочлен Ньютона
- •Властивості розділених різниць
- •Побудова інтерполяційного многочлена Ньютона
- •Приклад
- •Скінченні різниці
- •Формула залишкового члена інтерполяційного многочлена Лагранжа
- •Інтерполяції за допомогою раціональних функцій
- •Інтерполювання періодичних функцій
- •Інтерполяційний многочлен Ерміта
- •Збіжність інтерполяційних процесів
- •Інтерполяція сплайнами
Методи розв’язання системи лінійних рівнянь (слр). Прямі методи слр.
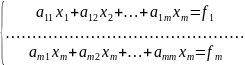 (1)
A=
(1)
A=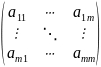
X= f=
f= Ax=f (2)
Ax=f (2)
Серед відомих прямих методів розв’язок існує розв’язок х. Для відшуканих розв’язків за методом Крамера нам потрібно виконати порядку m! Арифметичних дій, тоді ж як при використанні метода Гауса менше 0(м2). Тому,при достатньо великих м спосіб,який базується на обчисленні визначника,є набагато складнішим, ніж метод Гауса, тому що для розв’язання задач на ЕОМ широко використовують метод Гауса у всіх його модифікаціях.
Для розв’язання системи (1) методи можемо поділити на дві групи:
Прямі.
Ітераційні.
У прямих методах розв’язок системи (1) шукається в скінченному числі кроків,причому одержаний точний розв’язок системи,якщо всі ітерації виконані точно у зв’язку з заокругленням чисел. Про точний розв’язок на ЕОМ можемо говорити,якщо нехтувати похибками заокруглень. Систему методом Гауса може бути розв’язано до 100-го порядку.
Ітераційні
методи полягають в тому,що розв'язок х
системи (1) буде знаходитись як
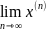 послідовних
наближень,де n
- номер ітерації.
послідовних
наближень,де n
- номер ітерації.
Як
правило, за скінченне число кроків дана
границя не одержується,тому задається
достатньо мале число ε і обчислення
будуть проводитися
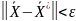 або ж може задаватися наперед кількість
крокі і тоді при досягнення кількості
кроків обчислювальний процес не
переривається і одержаний розв’язок
на останній ітерації приймається за
найближче значення розв’язку системи
(1).
або ж може задаватися наперед кількість
крокі і тоді при досягнення кількості
кроків обчислювальний процес не
переривається і одержаний розв’язок
на останній ітерації приймається за
найближче значення розв’язку системи
(1).
Метод Гауса чисельного розв’язку слр.
Ідея
методу полягає в наступному: послідовно
викидаються із системи змінні
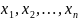 .
Припускаємо,що
.
Припускаємо,що
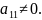 Тоді поділимо перше рівняння системи
(1) на
Тоді поділимо перше рівняння системи
(1) на
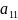 матимемо:
матимемо:
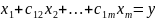 1
(3)
1
(3)
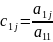 j=2,…,n
y1=
j=2,…,n
y1=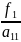
Всі
інші рівняння можуть бути записані
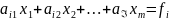 (4) i=1,…,n
(4) i=1,…,n
Рівняння
(3) множимо на
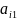 і додаємо до кожного рівняння (4) і тоді
ми одержимо:
і додаємо до кожного рівняння (4) і тоді
ми одержимо:
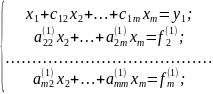 (5)
(5)
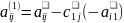 (6)
(6)
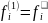 +
+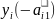 I,j=2,…,m
I,j=2,…,m
Перехід від (1) до (5) здійснюється за допомогою формули (6
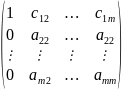
Розглянемо укорочену систему із системи (5)
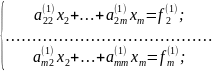 (7)
(7)
Якщо
у (7)
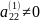 тоді перше рівняння (7) ділимо на
тоді перше рівняння (7) ділимо на
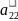 і виключаємо всіх невідомих.
і виключаємо всіх невідомих.
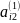 і=3,…,m
і=3,…,m
По аналогії робиться перетворення виключаючи невідомі x3,…,xm в результаті чого одержимо систему (8):
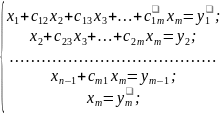 (8)
(8)
Матриця,яка відповідає даній системі з нулями вище головної діагоналі система складає прямий хід метода Гауса. Тоді обернений хід методу Гауса може бути записаний:
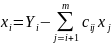 i=m-1,…,1
i=m-1,…,1
Вивід розрахункових формул
Ми припускаємо,що у нас є виконано к-1 крок метода Гауса.
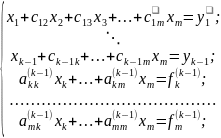 (9)
(9)
Розглянемо
к-ве рівняння системи (9) і припускаємо,
шо
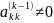 .Поділимо
к-ве рівняння системи на цей елемент. В
результаті чого ми одержимо рівняння:
.Поділимо
к-ве рівняння системи на цей елемент. В
результаті чого ми одержимо рівняння:
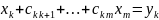 (10)
(10)
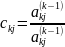 ;
j=k+1,…,m;
;
j=k+1,…,m;
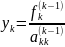 ;
;
Якщо
помножити рівняння (10) на -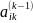 (i=k+1,…,m)
і додати до рівняння системи (9),
починаючи з к+1
до m-го
,тоді одержимо
(i=k+1,…,m)
і додати до рівняння системи (9),
починаючи з к+1
до m-го
,тоді одержимо
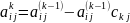
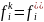 I,j=k+1,…,m
I,j=k+1,…,m
Тоді послідовність операцій у методі Гауса буде виконуватись за наступним правилом:
П1:
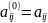 I,j=1,…,m (11)
I,j=1,…,m (11)
П2:
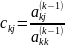 j=k+1,…,m (12) k=1,…,m
j=k+1,…,m (12) k=1,…,m
П3:
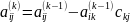 j=1,…,m
j=1,…,m
П4:
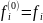 i=1,…,m
i=1,…,m
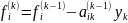 (14)
(14)
П1-П4 складає прямий хід методу Гауса.
