2.4. Диференціювання та інтегрування комплексної функції дійсної змінної

Комплексній змінній відповідає вектор-функція, тому диференціювання та інтегрування комплексної функції дійс­ної змінної здійснюється аналогічно відповідним операціям над вектор-функцією дійсного аргументу.

Для знаходження похідної комплексної функції дійсної змінної треба продиференціювати окремо дійсну та уявну частини:

.

Зауваження 1. На комплексній площині дотична до кривої в точці задається в комплексно-парамет­рич­ній формі рівнянням .

Приклад 1. Знайти рівняння дотичної до комплексно-пара­мет­рично заданої лінії в точці , що відповідає указаному значенню параметра :

, .

Розв’язання. 

;

;

;

– дотична.

Для знаходження інтеграла комплексної функції дійсної змінної треба проінтегрувати окремо дійс­ну та уявну частини:

.

Приклад 2. Знайти інтеграл:

.

Розв’язання. 

.

3. Функції комплексної змінної. Похідна.

Поняття аналітичної функції. Конформне відображення

3.1. Поняття функції комплексної змінної.

Границя та неперервність

Для геометричного тлумачення поняття функції комплексної змінної розглядаються два екземпляри площини комплексних чисел: -площина і -площина .

Нехай на -площині задана довільна множина точок . Якщо кожній точці множини за певним законом поставлено у відповідність одну точку (або де­кіль­ка точок) -площини, то говорять, що на множині задано однозначну (або багатозначну) комплексну функцію комплексної змінної . називається множиною визначення функції , а множина усіх значень , що прий­має функція, називається множиною значень функції .

Зауваження 1. Множина може бути дуже складної та різ­номанітної структу­ри. Надалі розглядаються лише випадки, коли множини та є областями.

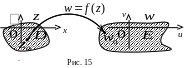
Комплексна функція – це відображення області -площини на область -площини (рис. 15). Якщо функція відображає точку площини в точку площини , то називається образом , а – прообразом.

Нерухомою точкою відображення називається така точка , що .

Приклад 1. Знайти нерухомі точки заданого відображення:

.

Розв’язання. Нерухомі точки визначаємо як корені рівняння

: ; ; .

Відображення називається взаємно одно­знач­ним або однолистим в області , якщо довільним двом різним точкам області завжди відповідають дві різні точки області . У цьоиу випадку існує обернена функція – відображення області на область .

Зауваження 2. Відображення є однолистим тоді і тільки тоді, коли пряма і обернена функції однозначні.

Зауваження 3. Задання комплексної функції комплексної змінної , де – комплексний аргумент, – комплексна залежна змінна, рівносильне заданню упорядкованої пари дійсних функцій двох дійсних змінних і . Тому поняття границі та неперервності функції комплексної змінної вводяться так само, як і відпо­відні поняття для функції дійсних змінних. Це дозволяє перенести на комплексні функції основні теореми дійсного аналізу.

Приклад 2. Знайти образи заданих ліній при відображенні функцією :

а) пряма ; б) коло ; в) промінь .

Розв’язання.  ; ;

;

; ;

а) пряма : ; ; ; ;

– парабола (образ прямої ).

б) коло : ;

– коло (образ кола ).

в) промінь : ;

– промінь (образ променя ).

Зауваження 4. Відображення , що однолисте і неперервне в замкненій області , переводить цю область в деяку замкнену область . При цьому межа області перехо­дить в межу області зі збереженням напряму обходу (принцип збереження напряму обходу).