7.4. Логарифмічна похідна та її лишки. Принцип аргументу

Похідна логарифму функції називається логарифмічною похідною

.

Логарифмічним лишком функції називається лишок її логарифмічної похідної.

Розвиваючи логарифмічну похідну в ряд Лорана в околі кореня функції , можна отримати, що -кратний корінь функції також служить простим полюсом її логарифмічної похідної, причому

.

Розвиваючи логарифмічну похідну в ряд Лорана в околі полюса функції , можна отримати, що полюс -го порядку функції служить простим полюсом її логарифмічної похідної, причому

.

Теорема (Принцип аргументу). Нехай ‑ обмежена однозв’язна область, ‑ її межа, а функція аналітична в замкненій області за винятком скінченного числа полюсів, причому на межі немає ні коренів, ні полюсів цієї функції. Тоді приріст аргументу функції при однократному обході межі області в додатному напрямі дорівнює добутку числа на різницю числа коренів і полюсів функції , причому кожний корінь рахується стільки разів, яка його кратність, а полюс – стільки разів, який його порядок:

.

Зауваження 1. Число коренів скінченне, інакше функція тотожно дорівнювала б нулю. Число полюсів скінченне, інакше функція мала б неізольовану особливість.

Зауваження 2. Аргумент функції визначається неодно­значно, але його приріст на кривій знаходиться однозначно при будь-якому фіксованому початковому (зокрема, головному) значенні аргументу.

8. Фазові криві диференціальних рівнянь

8.1. Лінійне однорідне диференціальне рівняння зі сталим комплексним коефіцієнтом і його розв’язок

Лінійне однорідне диференціальне рівняння зі сталим комп­лексним коефіцієнтом має вигляд

,

де  – сталий коефіцієнт (комплексне число);  – шукана комп­лексна функція дійсного аргументу .

Відокремлюючи змінні, можна знайти його загальний роз­в’язок

,

де  – довільна комплексна стала.

Як і в дійсному випадку, розв’язком рівняння служить експо­нента (при ) – єдина відмінна від тотожного нуля функція, в якої похідна пропорційна їй самій, а також тотожний нуль (при ). Інших розв’язків рівняння не має.

Зауваження. Рівняння можна розв’язати інакше, як­що виділити дійсну та уявну частини і перейти до рівносильної системи двох дійсних рівнянь:

;

; .

8.2. Фазові криві лінійного однорідного диференціального рівняння

Інтегральними кривими даного диференціального рівнян­ня служать графіки його загального розв’язку в тривимірному просторі , утвореному незалежною змінною і двома залежними змінними і . Інтеграль­ні криві утворюють однопараметричну сім’ю ліній. Кожна інтегральна крива цієї сім’ї є графіком частинного розв’язку, що відповідає конкретному значенню довільної сталої – парамет­ра.

Проекція інтегральної кривої на площину залежних змінних (комплексну площину) називається фазовою кривою.

Зауваження. Різні фазові криві, як і відповідні інтегральні криві, ніколи не перетинаються.

Розглянемо фазові криві на комплексній площині, де задано декартову і полярну системи координат з полюсом у початку декартової системи координат і полярною віссю, суміщеною з віссю .

При довільному значенні коефіцієнта рівняння завжди має сталий (нерухомий) розв’язок – по­люс (при нульовому значенні довільної сталої – початкової точки ).

Нехай тепер довільна стала (початкова точка) відмінна від нуля . Подамо її, а також ненульовий експоненціальний розв’язок у показниковій формі:

; .

Тоді

;

; .

а) Якщо коефіцієнт  – дійсне число, тобто , тоді для ненульового розв’язку полярний кут залишається сталим , а полярний радіус . Таким чином, при зміні відбувається переміщення від початкової точки по променю : вбік віддалення від полюса при чи вбік наближення до полюса при (рис. 34). Такий вигляд картини фазових кривих називається нестійким (при ) чи стійким (при ) вузлом.

б) Якщо коефіцієнт  – чисто уявне число, тобто , , тоді для ненульового розв’язку полярний радіус залишається сталим , а полярний кут . Таким чином, при зміні відбувається обертання від початкової точки по колу з центром у полюсі: проти годинникової стрілки при чи за годинниковою стрілкою при (рис. 35). Такий вигляд картини фазових кривих нази­вається центром.

в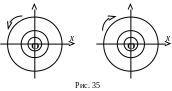 ) Якщо в коефіцієнті відмінні від нуля як дійсна , так і уявна частини, тоді для ненульового роз­в’язку змінюються як полярний кут , так і полярний радіус . Таким чином, при зміні відбувається на­кладання обертального руху навколо полюса з віддаленням чи наближенням до полюса, починаючи від початкової точки : проти годинникової стрілки при чи за годинниковою стрілкою при (рис. 36). Фазовими кривими служать логарифмічні спіралі. Такий вигляд картини фазових кри­вих на­зивається нестійким (при ) чи стійким (при ) фокусом.